Как известно, соответствующий раздел в школьном курсе геометрии изучается уже в 7 классе. Однако, для многих школьников этот материал оказывается трудным для запоминания. В результате на экзамене, будь то ЕГЭ или дополнительное вступительное испытание по математике в вузе, бедному сдающему приходится в муках вспоминать, что же он изучал по этой теме в далеком 7 классе. К сожалению, зачастую безуспешно. Решим эту проблему раз и навсегда! Ниже приведен основный справочный материал по данной важнейшей теме школьного курсе геометрии от репетитора по математике и физике.
Накрест лежащие прямые при параллельных прямых
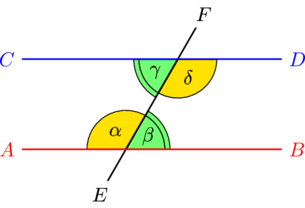
На рисунке углы ![]() и
и ![]() , а также
, а также ![]() и
и ![]() являются накрест лежащими при прямых
являются накрест лежащими при прямых ![]() ,
, ![]() и секущей
и секущей ![]() . Если прямая
. Если прямая ![]() параллельна прямой
параллельна прямой ![]() , то
, то ![]() и
и ![]() (свойство параллельных прямых). Верно и обратное. Если
(свойство параллельных прямых). Верно и обратное. Если ![]() или
или ![]() , то прямая
, то прямая ![]() параллельна прямой
параллельна прямой ![]() (признак параллельности прямых).
(признак параллельности прямых).
Соответственные углы при параллельных прямых
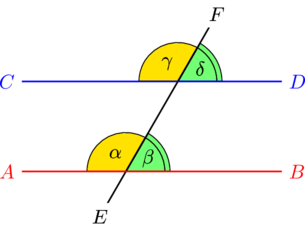
На рисунке углы ![]() и
и ![]() , а также
, а также ![]() и
и ![]() являются соответственными при прямых
являются соответственными при прямых ![]() ,
, ![]() и секущей
и секущей ![]() . Если прямая
. Если прямая ![]() параллельна прямой
параллельна прямой ![]() , то
, то ![]() и
и ![]() (свойство параллельных прямых). Верно и обратное. Если
(свойство параллельных прямых). Верно и обратное. Если ![]() или
или ![]() , то прямая
, то прямая ![]() параллельна прямой
параллельна прямой ![]() (признак параллельности прямых)
(признак параллельности прямых)
Односторонние углы при параллельных прямых
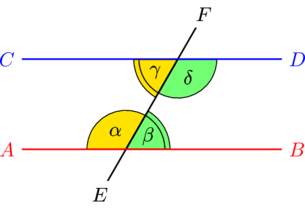
На рисунке углы ![]() и
и ![]() , а также
, а также ![]() и
и ![]() являются односторонними при прямых
являются односторонними при прямых ![]() ,
, ![]() и секущей
и секущей ![]() . Если прямая
. Если прямая ![]() параллельна прямой
параллельна прямой ![]() , то
, то ![]() и
и ![]() (свойство параллельных прямых). Верно и обратное. Если
(свойство параллельных прямых). Верно и обратное. Если ![]() или
или ![]() , то прямая
, то прямая ![]() параллельна прямой
параллельна прямой ![]() (признак параллельности прямых).
(признак параллельности прямых).
| Tantum possumus, quantum scimus — (лат.) мы можем столько, сколько знаем. (Ф. Бэкон) |

Лучше на рисунке обозначить неравные углы не только цветом, но и разным количеством дуг, как обычно делают в школьных учебниках по геометрии.
Спасибо за рекомендацию, так и сделал. Благо Tikz это позволяет сделать без проблем 🙂