ДВИ по математике в МГУ за 2014 год

Автор

Среда, 22 июля, 2015

Главное здание МГУ на фоне голубого неба

В статье приведен подробный разбор заданий одного из вариантов дополнительного вступительного испытания по математике, проведенного в МГУ в 2014 году. На выполнение отводилось 4 астрономических часа, а результаты оценивались проверяющими по 100-бальной шкале. На официальном сайте центральной приемной комиссии МГУ указано, что объем знаний, необходимых для выполнения предлагаемых заданий, соответствовал курсу математики средней школы. Сдающий был вправе использовать весь арсенал средств из этого курса, включая и начала анализа. При этом поступающий также мог использовать математические факты и понятия, выходящие за рамки курса математики общеобразовательной школы, но в этом случае их необходимо было пояснять и доказывать.

Задача 1. Найдите в явном виде натуральное число, заданное выражением \sqrt{7-4\sqrt{3}}\left(8+4\sqrt{3}\right).

Решение. Упростим первый множитель:

    \[ \sqrt{7-4\sqrt{3}} = \sqrt{2^2-2\cdot 2\sqrt{3}+\left(\sqrt{3}\right)^2} = \]

    \[ = \sqrt{\left(2-\sqrt{3}\right)^2} = \left|2-\sqrt{3}\right| = 2-\sqrt{3}. \]

Тогда выражение примет вид:

    \[ \left(2-\sqrt{3}\right)\left(8+4\sqrt{3}\right) = 16 + 8\sqrt{3} - 8\sqrt{3} - 12 = 4. \]

Ответ: 4.

Задание 2. Найдите максимальное значение функции \log_{\frac{1}{2}}\left(x^2-6x+17\right).

Решение. Функция y=\log_{\frac{1}{2}}x является убывающей, поскольку основание логарифма 0<\frac{1}{2}<1. Следовательно, она принимает свое максимальное значение, когда ее аргумент принимает минимальное значение. Поэтому ищем наименьшее значение выражения x^2-6x+17.

Ветви соответствующей параболы направлены вверх, абсцисса вершины равна 3. Тогда наименьшее значение выражения равно 8. Окончательно, \log_{\frac{1}{2}}8=-3.

Ответ: -3.

Задание 3. Найдите все положительные x, удовлетворяющие неравенству x^{3x+7}>x^{12}.

Решение. Данное неравенство при положительных x равносильно следующей совокупности:

    \[ \left[ \begin{array}{l} \begin{cases} 0<x<1, \\ 3x+7<12. \end{cases} \\ \begin{cases} x=1, \\ 1>1. \end{cases} \\ \begin{cases} x>1, \\ 3x+7>12. \end{cases} \end{array} \Leftrightarrow \left[ \begin{array}{l} 0<x<1, \\ x>\frac{5}{3}. \end{array} \]

Ответ: x\in(0;1)\cup\left(\frac{5}{3};+\mathcal{1}\right).

Задание 4. Решите уравнение:

    \[ \cos^2x-\cos x\sin^2\left(\frac{5x}{4}-\frac{5\pi}{12}\right)+\frac{1}{4}=0. \]

Решение. Данное уравнение можно рассматривать как квадратное относительно \cos x. Тогда дискриминант это уравнения:

    \[ \sin^4\left(\frac{5x}{4}-\frac{5\pi}{12}\right)-1\leqslant 0. \]

То есть решение исходное уравнение имеет только в том случае, если этот дискриминант равен 0:

    \[ \sin^4\left(\frac{5x}{4}-\frac{5\pi}{12}\right)=1\Leftrightarrow \]

(1)   \begin{equation*} \sin^2\left(\frac{5x}{4}-\frac{5\pi}{12}\right)=1 \end{equation*}

В этом случае исходное уравнение принимает вид:

    \[ \cos^2x-\cos x+\frac{1}{4}=0\Leftrightarrow \]

    \[ \cos x = \frac{1}{2},\Leftrightarrow x =\pm\frac{\pi}{3}+2\pi n,\, n\in Z. \]

Из этого множества выбираем те значения, при которых выполняется условие (1):

При x=\frac{\pi}{3}+2\pi n:

    \[ \sin^2\left(\frac{5\pi}{12}-\frac{5\pi}{12}+\frac{5\pi n}{2}\right) = 1\left|_{n=2k+1,\,k\in Z}. \]

При x=-\frac{\pi}{3}+2\pi n:

    \[ \sin^2\left(-\frac{5\pi}{12}-\frac{5\pi}{12}+ \frac{5\pi n}{2}\right) = \sin^2\left(-\frac{5\pi}{6}+ \frac{5\pi n}{2}\right)\ne 1 . \]

Итак, подходят только x=\frac{\pi}{3}+2\pi(2k+1)=\frac{7\pi}{3}+4\pi k.

Ответ: x=\frac{7\pi}{3}+4\pi k.

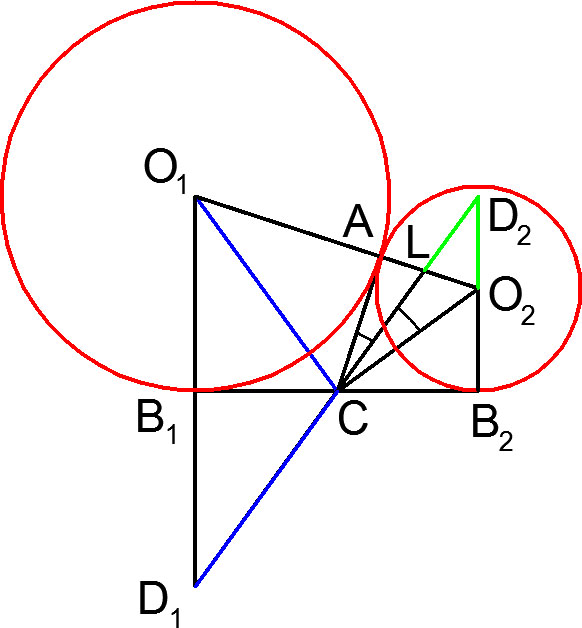
Задание 5. Окружности \Omega_ и \Omega_2 с центрами в точках O_1 и O_2 касаются внешним образом в точке A. Общая внешняя касательная к этим окружностям касается  \Omega_ и \Omega_2 соответственно в точках B_1 и B_2. Общая касательная к окружностям, проходящая через точку A, пересекает отрезок B_1B_2 в точке C. Прямая делящая угол ACO_2 пополам, пересекает прямые O_1B_1, O_1O_2, O_2B_2 в точках D_1, L, D_2 соответственно. Найти отношение LD_2:O_2D_2, если известно, что CD_1=CO_1.

Решение. Самое главное в этой задаче — правильный рисунок:

Рисунок для геометрической задачи из вступительного в МГУ 2014

Для решения задачи нам потребуются следующие факты:

1. Прямоугольные треугольники O_1CB_1 и B_1CD_1 равны по гипотенузе и катету, поэтому \angle B_1CD_1 = \angle B_1CO_1.

2. Прямоугольные треугольники O_1B_1C и O_1CA равны по гипотенузе и катету, поэтому \angle B_1CO_1 = \angle O_1CA. Аналогично, прямоугольные треугольники ACO_2 и O_2CB_2 равны, поэтому \angle ACO_2 = \angle O_2CB_2.

3. \angle O_1CO_2 = 90^0. Доказательство этого факта можно найти в данной статье (задача 1).

Введем следующие обозначения:

    \[ \angle D_1CB_1 = \angle B_1CO_1 = \angle O_1CA = \angle D_2CB_2 = \alpha, \]

    \[ \angle ACL = \angle LCO_2 = \beta. \]

Найдем градусную меру углов \alpha и \beta. Для этого рассмотрим следующие углы:

    \[ \angle D_1CL = 180^0 = 3\alpha + \beta, \]

    \[ \angle O_1CO_2 = 90^0 = \alpha + 2\beta. \]

То есть имеет место следующая система:

    \[ \begin{cases} 3\alpha+\beta = 180^0, \\ \alpha+2\beta = 90^0. \end{cases} \Leftrightarrow \begin{cases} \alpha = 54^0, \\ \beta = 18^0. \end{cases} \]

Теперь ищем градусную меру \angle D_2O_2L и \angle D_2LO_2:

    \[ \angle D_2O_2L = 180^0-2(90^0-\alpha+\beta) = 72^0, \]

    \[ \angle D_2LO_2 = \angle ALC = 90^0-\beta = 72^0. \]

Итак, треугольник LD_2O_2 — равнобедренный, поэтому LD_2=D_2O_2. То есть искомое отношение LD_2:D_2O_2 = 1.

Ответ: 1

Задание 6. Найдите все положительные x, y, удовлетворяющие системе уравнений

    \[ \begin{cases} x^{\frac{3}{2}}+y=16,\\ x+y^{\frac{2}{3}}=8. \end{cases} \]

Решение. Введем следующую замену: a=x^{\frac{1}{2}}, b=y^{\frac{1}{3}}. Тогда система принимает следующий вид:

    \[ \begin{cases} a^3+b^3=16, \\ a^2+b^2=8. \end{cases} \]

Представим систему в виде:

    \[ \begin{cases} (a+b)(a^2-ab+b^2)=16, \\ (a+b)^2-2ab=8. \end{cases}\Leftrightarrow \begin{cases} (a+b)(8-ab)=16, \\ (a+b)^2-2ab=8. \end{cases} \]

Вновь замена: m=a+b, n=ab.

    \[ \begin{cases} m(8-n)=16, \\ m^2-2n=8. \end{cases}\Leftrightarrow \begin{cases} m(8-n)=16, \\ m^2-2n=8. \end{cases} \]

В положительных числах решение будет m=n=4. Первая обратная замена даёт a=b=2. Вторая обратная замена даёт x=4, y=8.

Ответ: (4;8).

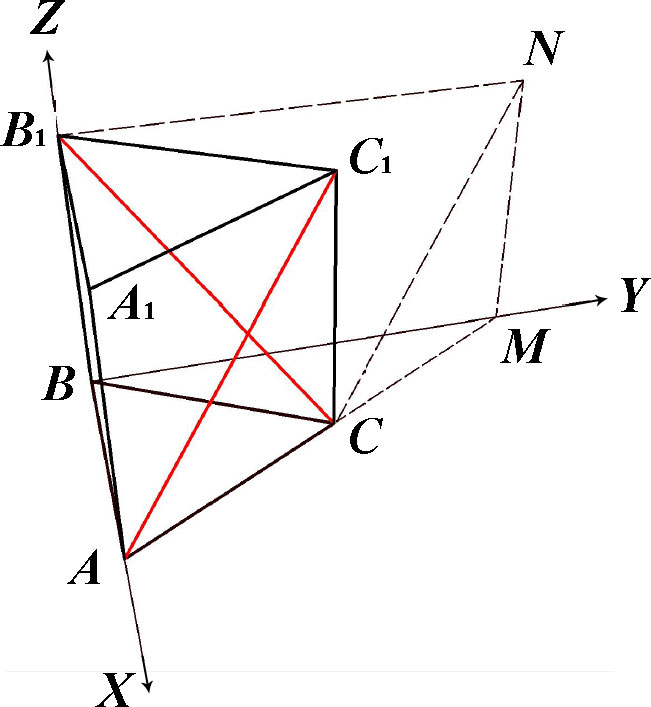
Задание 7. В основании прямой призмы лежит правильный треугольник со стороной 1. Высота призмы равна \sqrt{2}. Найдите расстояние между скрещивающимися диагоналями боковых граней.

Решение. Для большей наглядности приведем рисунок к данному заданию:

Чертеж к заданию

Введем систему координат, как показано на рисунке. Через точку C проведем прямую, параллельную AC_1. Точку пересечения этой прямой и плоскости A_1B_1C_1 обозначим буквой N. Тогда по построению плоскость CNB_1 параллельна прямой AC_1 (так как последняя параллельна прямой CN, лежащей в этой плоскости). Тогда ищем расстояние от прямой AC_1 до этой плоскости. Это и будет искомое расстояние между скрещивающимися прямыми.

В данной системе координат имеем следующие координаты точек: B_1(0;0;\sqrt{2}), C(\frac{1}{2};\frac{\sqrt{3}}{2};0), N(0;\sqrt{3};\sqrt{2}), A(1;0;0). Тогда для точек плоскости CNB_1 имеем следующую систему:

    \[ \begin{cases} \sqrt{2}C+D=0, \\ \frac{1}{2}A+\frac{\sqrt{3}}{2}B+D=0,\\ \sqrt{3}B+\sqrt{2}C+D=0. \end{cases} \Leftrightarrow \begin{cases} C=-\frac{D}{\sqrt{2}},\\ B=0,\\ A=-2D. \end{cases} \]

Тогда уравнение плоскости CNB_1 в данной системе координат имеет вид: -2Dx-\frac{D}{\sqrt{2}}z+D=0 или 2x+\frac{1}{\sqrt{2}}z-1=0.

Тогда искомое расстояние равно:

    \[ d=\frac{\left|1\cdot 2 - 1\right|}{\sqrt{2^2+\left(\frac{1}{\sqrt{2}}\right)^2}}=\frac{\sqrt{2}}{3}. \]

Ответ: \frac{\sqrt{2}}{3}.

Задание 8. Пусть

    \[ f(x,y)=\sqrt{-6x^2-14y^2-18xy+6}+y \]

    \[ g(x,y)=-\sqrt{-6x^2-14y^2-18xy+6}+y. \]

Найдите все значения, которые может принимать хотя бы одна из этих функций.

Решение. Задание можно переформулировать следующим образом: найдите все значения t, удовлетворяющие совокупности:

    \[ \left[ \begin{array}{l} t-y = \sqrt{-6x^2-14y^2-18xy+6}, \\ t-y = -\sqrt{-6x^2-14y^2-18xy+6}. \end{array} \]

Данная совокупность равносильна уравнению:

    \[ (t-y)^2 = -6x^2-14y^2-18xy+6\Leftrightarrow \]

    \[ 6x^2 + 18xy + (t-y)^2 + 14y^2 - 6 = 0. \]

Данное уравнение имеет корни относительно x, когда его дискриминант неотрицателен:

    \[ (18y)^2-24((t-y)^2+14y^2-6)\geqslant 0\Leftrightarrow \]

    \[ 3y^2-4yt+2t^2-12\leqslant 0. \]

Последнее неравенство, в свою очередь, разрешимо относительно y, когда его дискриминант неотрицателен:

    \[ (4t)^2-12(2t^2-12)\geqslant 0\Leftrightarrow \]

    \[ t^2\leqslant 18\Leftrightarrow t\in\left[-3\sqrt{2};3\sqrt{2}\right]. \]

Ответ: \left[-3\sqrt{2};3\sqrt{2}\right].

Репетитор по математике
Сергей Валерьевич

Метки: , ,
Опубликовано в категории Методическая копилка | 19 комментариев »

Комментарии

  1. Алика:
    30.04.2016 в 15:16

    Здравствуйте, во 2 задании. Если подставить любое число от (0;1) неравенство не будет меньше

    Если подставить x=1/3, то будет ((1/2)^(1+7))>((1/2)^12) ,знак будет меньше

    Ответить
    1. Алика:
      30.04.2016 в 15:17

      Ошиблась x=1/3, то (1/3)^8<(1/3)^12

      Ответить
      1. Сергей:
        30.04.2016 в 15:23

        Здравствуйте, имеется ввиду, видимо, задание 3. При x=1/3 получаем (1/3)^8>(1/3)^12.

        Ответить
        1. Алика:
          30.04.2016 в 15:54

          Да, решением же не является данный промежуток (1/3)^8=1.524157902758…, a (1/3)^12=1.88167642315892074…

          Ответить
          1. Сергей:
            30.04.2016 в 15:59

            (1/3)^8=0.0001524157902…, а (1/3)^12=1.8816764…× 10^-6 = 0.0000018816764… Там, где Вы считаете, степень посмотрите. http://www.wolframalpha.com/input/?i=(1%2F3)%5E8

  2. дюд которого задолбали цифры:
    11.07.2016 в 01:07

    если разбирать, то разбирайте подробно с пояснениями, если черт возьми я понимаю как решать, то вы мне нахрен не сдались!!!
    в неравенстве все упрощали упрощали и тут бах сразу ответ, горите в аду все математики !!!

    Ответить
    1. Сергей:
      11.07.2016 в 12:25

      Предполагалось, что для абитуриентов, поступающих в МГУ, не требуется разжёвывания всех деталей. Они, по идее, должны быть в теме.

      Ответить
    2. Александр:
      13.07.2016 в 20:12

      Не соглашусь. Представленные решения понятные и наглядные, лучше официальных. Отдельное спасибо за стереометрию, кстати.

      Ответить
      1. Сергей:
        13.07.2016 в 22:10

        Рад, что статья оказалась полезной.

        Ответить
  3. Мария:
    14.07.2016 в 12:51

    Подскажите, почему в 5 задаче О1О2 обязательно проходит через А?

    Ответить
    1. Сергей:
      15.07.2016 в 00:18

      Ну, например, можно так доказать. OA и O1A — радиусы двух окружностей, проведённые в точку касания к общей касательной AC. Оба радиуса перпендикулярны этой касательной. Тогда угол O1AO2 равен сумме двух прямых углов, поэтому равен 180 градусам. Следовательно отрезки O1A и AO2 лежат на одной прямой.

      Ответить
  4. Яна:
    26.03.2017 в 11:35

    В восьмом задании ошибка — когда переносили 6 из левой части уравнения в правую, — не поставили

    Ответить
    1. Сергей:
      26.03.2017 в 16:14

      Да, спасибо. Это была опечатка. На дальнейшие вычисления и ответ она не повлияла.

      Ответить
  5. коля:
    03.05.2017 в 23:05

    Извините, но не могли бы вы объяснить в 4 задании почему n=2k+1

    Ответить
    1. Сергей:
      04.05.2017 в 22:58

      Ну потому что выражение sin^2(5*pi*n/2) равно 1 только при нечётных n.

      Ответить
  6. Абитуриент:
    03.07.2017 в 14:09

    В 7 задании в конце вы ищите расстояние от точки А до нужной плоскости, почему именно от этой точки, а не от вектора?

    Ответить
    1. Сергей:
      03.07.2017 в 16:05

      Можно взять любую точку прямой AC1, потому что она параллельна этой плоскости. У точки A просто очень удобные координаты.

      Ответить
  7. Марк:
    01.02.2020 в 16:45

    7задание. Можете сказать, как бы вы обосновали, что надо искать расстояние от прямой до построенной плоскости. То есть я понимаю, что растояние между построенной прямой и диагональю равно 0,так как они перпендикулярны, но вот почему ищем данные значения?

    Ответить
    1. Сергей Валерьевич:
      02.02.2020 в 09:04

      Посмотрите в этой статье, там всё расписано.

      Ответить

Добавить комментарий