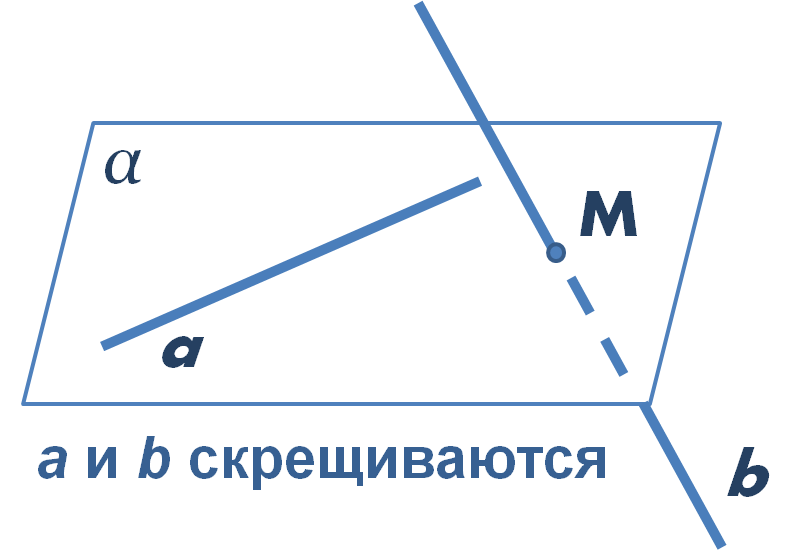
В данной статье на примере решения задачи C2 из ЕГЭ разобран способ нахождения расстояния между скрещивающимися прямыми с помощью метода координат. Напомним, что прямые являются скрещивающи-мися, если они не лежат в одной плоскости. В частности, если одна прямая лежит в плоскости, а вторая прямая пересекает эту плоскость в точке, которая не лежит на первой прямой, то такие прямые являются скрещивающимися (см. рисунок).
Для нахождения расстояния между скрещивающимися прямыми необходимо:
- Провести через одну из скрещивающихся прямых плоскость, которая параллельна другой скрещивающейся прямой.
- Опустить перпендикуляр из любой точки второй прямой на полученную плоскость. Длина этого перпендикуляра будет являться искомым расстоянием между прямыми.
Разберем данный алгоритм подробнее на примере решения задачи C2 из ЕГЭ по математике.
Расстояние между прямыми в пространстве
Задача. В единичном кубе ABCDA1B1C1D1 найдите расстояние между прямыми BA1 и DB1.
Решение. Через середину диагонали куба DB1 (точку O) проведем прямую, параллельную прямой A1B. Точки пересечения данной прямой с ребрами BC и A1D1 обозначаем соответственно N и M. Прямая MN лежит в плоскости MNB1 и параллельна прямой A1B, которая в этой плоскости не лежит. Это означает, что прямая A1B параллельна плоскости MNB1 по признаку параллельности прямой и плоскости (рис. 2).
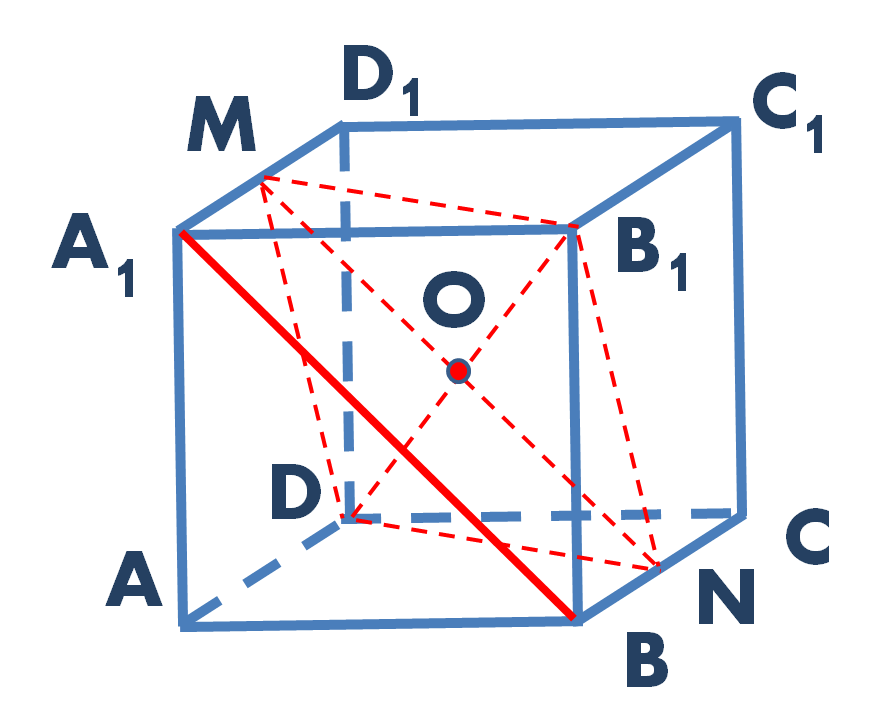
Рис. 2. Искомое расстояние между скрещивающимися прямыми равно расстоянию от любой точки выделенной прямой до изображенной плоскости
Ищем теперь расстояние от какой-нибудь точки прямой A1B до плоскости MNB1. Это расстояние по определению будет являться искомым расстоянием между скрещивающимися прямыми.
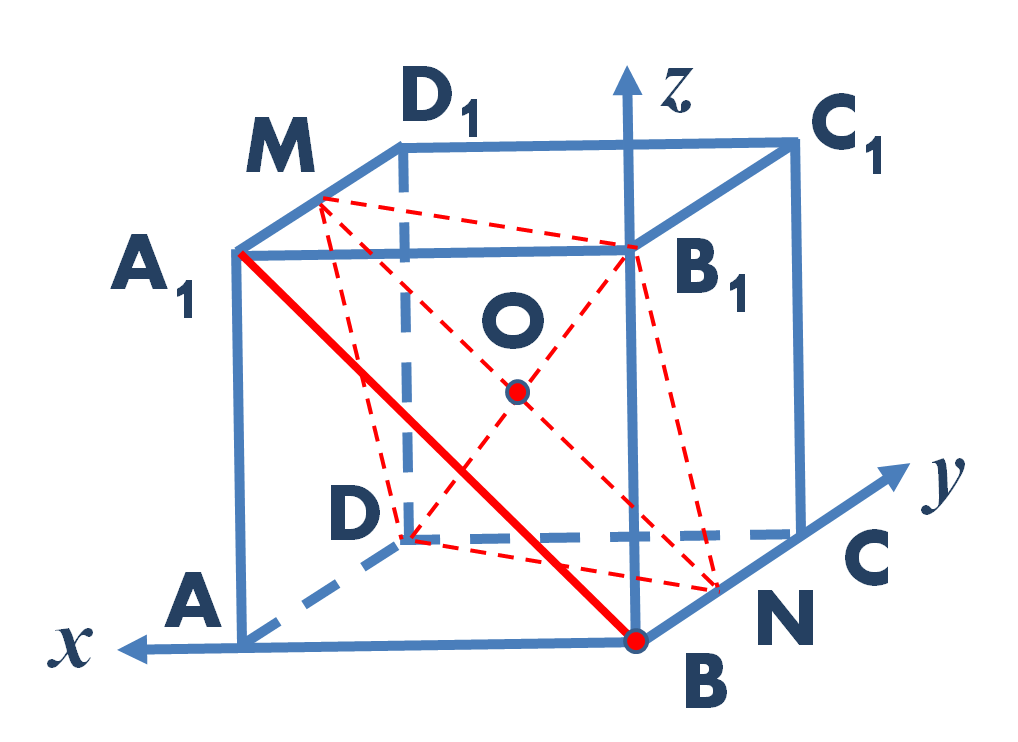
Для нахождения этого расстояния воспользуемся методом координат. Введем прямоугольную декартову систему координат таким образом, чтобы ее начало совпало с точкой B, ось X была направлена вдоль ребра BA, ось Y — вдоль ребра BC, ось Z — вдоль ребра BB1 (рис. 3).
Находим уравнение плоскости MNB1 в данной системе координат. Для этого определяем сперва координаты точек M, N и B1: ![]()
![]()
![]() Полученные координаты подставляем в общее уравнение прямой
Полученные координаты подставляем в общее уравнение прямой ![]() и получаем следующую систему уравнений:
и получаем следующую систему уравнений:
![Rendered by QuickLaTeX.com \[ \begin{cases}a\cdot 1+b\cdot \frac{1}{2}+c\cdot 1 + d = 0, \\ a\cdot 0+b\cdot \frac{1}{2}+c\cdot 0 + d = 0, \\ 0\cdot 1+b\cdot 0+c\cdot 1 + d = 0.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e089db7d19582bb1ee128bfcabd0b022_l3.png)
Из второго уравнения системы получаем ![]() из третьего получаем
из третьего получаем ![]() после чего из первого получаем
после чего из первого получаем ![]() Подставляем полученные значения в общее уравнение прямой:
Подставляем полученные значения в общее уравнение прямой:
![]()
Замечаем, что ![]() иначе плоскость MNB1 проходила бы через начало координат. Делим обе части этого уравнения на
иначе плоскость MNB1 проходила бы через начало координат. Делим обе части этого уравнения на ![]() и получаем:
и получаем:
![]()
Расстояние от точки до плоскости определяется по формуле:
![]()
где ![]() — координаты точки B.
— координаты точки B. ![]() — коэффициенты при переменных
— коэффициенты при переменных ![]() в уравнении плоскости. Точка B имеет координаты
в уравнении плоскости. Точка B имеет координаты ![]() Получаем окончательно:
Получаем окончательно:
![Rendered by QuickLaTeX.com \[ l = \frac{|1\cdot 0-2\cdot 0-1\cdot 0 + 1|}{\sqrt{1^2+(-2)^2+(-1)^2}}=\frac{1}{\sqrt{6}}=\frac{\sqrt{6}}{6}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-b0ce77d1513d51363c4922fcc802d45f_l3.png)
Ответ: ![]()
Сергей Валерьевич
Репетитор по геометрии в Тропарёво


Здравствуйте. У меня такой вопрос. Во второй части решения при вычислении расстояния от точки и плоскости нужно брать ЛЮБУЮ точку на прямой (в данном случае A1B) или середину этого отрезка?
Здравствуйте. Любую. Эта прямая параллельна плоскости, поэтому расстояние от любой ее точки до плоскости есть величина постоянная.
здравствуйте, подскажите как действовать если куб не единичный? как найти расстояние между получившейся плоскостью и прямой?
Абсолютно аналогично. Тут решение не привязано к тому, что он единичный. У Вас есть условие?
Отличное объяснение! Прочитал теоретическую часть, пошёл сам решать, и ответ сошёлся. Спасибо автору.
Скажите пожалуйста можно ли использовать определитель на ЕГЭ
Можно использовать то, что входит в программу по математике для общеобразовательных школ.
А ка же метод координат! Его же вроде нет в школьных учебниках. Например формула расстояния от точки до плоскости
Методом координат такие задачи решать можно, просто не всегда рационально. Иногда много проще решить геометрически. В любом случае, практика показывает, что знать, как эти задачи решаются координатным методом, чрезвычайно полезно.
Вы могли проходить метод координат и в школе на элективных курсах.Кстати, например, в сборнике «Подготовка ЕГЭ» под редакцией Лысенко Ф.Ф. есть краткий теоретический материал. Вот там Вы можете встретить эти формулы. Так что пользуйтесь смело. Успехов Вам.
Хочу внести уточнение. Метод координат есть. Просто не все формулы, применяемые в данном примере рассматриваются в базовом курсе геометрии.
Здравствуйте, спасибо большое, все по пунктикам расписано.
Используется одна формула. Она есть в учебнике Атанасяна стр. около 115
Большое спасибо!!!
Я немного не понимаю. Прямые А’B и MN параллельны, MN проходит через центр куба О. Значит точки M и N должны быть серединами ребер A’D’ и BC. То есть искомое расстояние должно быть расстоянием между параллельными прямыми A’B и MN. Это половина ребра куба. Почему найденное Вами расстояние не зависит от ребра куба?
Потому что куб единичный, то есть с длиной ребра 1.
Почему не зависит от ребра понятно.