Предлагаю на этот раз устроить что-то вроде «доказательного марафона» по решению задач, которые предлагаются девятиклассникам в вариантах ГИА по математике. Связаны они с доказательством несложных, но в то же время очень полезных геометрических фактов. В статье намеренно не приведены подробные решения задач, лишь некоторые наброски и подсказки. Постарайтесь преодолеть эту марафонскую дистанцию самостоятельно, без ошибок и за один подход.
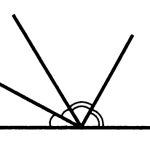
Задача 1. Докажите, что биссектрисы смежных углов перпендикулярны.
Доказательство: из рисунка видно, что α + α + β + β = 2α + 2β = 1800 (развернутый угол), следовательно, α + β = 900. Что и требовалось доказать.
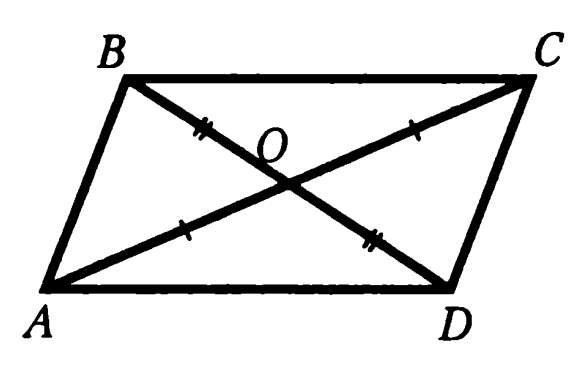
Задача 2. Два отрезка AC и BD пересекаются в точке O, которая является серединой каждого из них. Докажите равенство треугольников ACD и CAB.
Доказательство: боковые треугольники равны по двум сторонам и углу между ними (BO = OD — по условию, AO = OC — по условию, ∠DOC = ∠AOB — вертикальные), то есть ∠ACD = ∠CAB, а поскольку они являются накрест лежащими при прямых AB, CD и секущей AC, то AB параллельна DC. Аналогично доказываем параллельность прямых BC и AD. Итак, ABCD — параллелограмм по определению. BC = AD, AB = CD (в параллелограмме противоположные стороны равны), AC — общая для треугольников ACD и CAB, поэтому они равны по трем сторонам. Что и требовалось доказать.
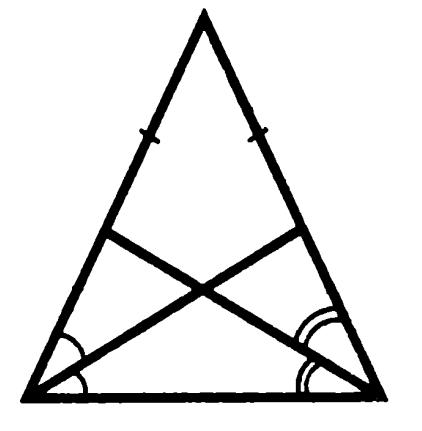
Задача 3. Докажите, что медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой угла, противолежащего основанию, а также перпендикулярна основанию.
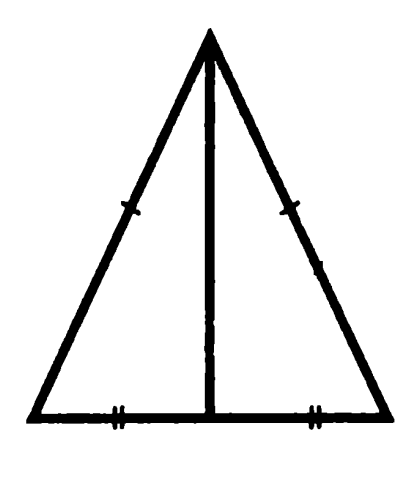
Углы, образованные медианой и основанием, назовем «нижними», медианой и боковыми сторонами — «верхними»
Доказательство: боковые треугольники на рисунке равны по трем сторонам, из чего следует равенство, во-первых, «верхних» углов (доказали, что биссектриса), во-вторых, «нижних» углов, в сумме как смежные дающих 1800, и равных поэтому по 900 каждый (доказали перпендикулярность). Что и требовалось доказать.
Задача 4. Докажите, что медианы, проведенные к боковым сторонам равнобедренного треугольника, равны.
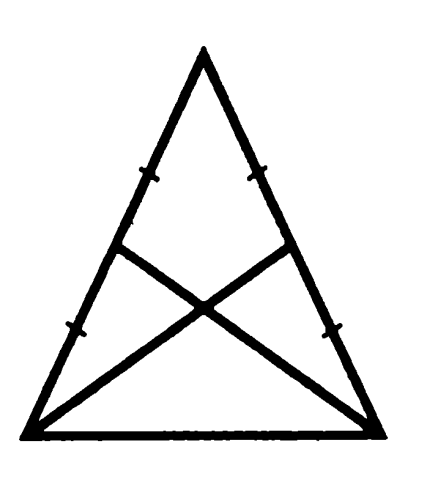
Треугольники, образованные медианами, основанием и нижними половинами боковых сторон исходного треугольника, назовем «нижними»
Доказательство: углы при основании равнобедренного треугольника равны, поэтому «нижние» треугольники равны по двум сторонам и углу между ними, из чего следует равенство проведенных медиан. Что и требовалось доказать.
Задача 5. Докажите, что биссектрисы, проведенные из вершин основания равнобедренного треугольника, равны.
Доказательство: «нижний» треугольник равнобедренный, что следует из равенства углов при его основании, «боковые» треугольники равны по стороне (равные из доказанного выше частички биссектрис) и двум углам (первые равны по условию, вторые как вертикальные), поэтому оставшиеся частички биссектрис также равны друг другу, а значит равны и сами биссектрисы целиком. Что и требовалось доказать.
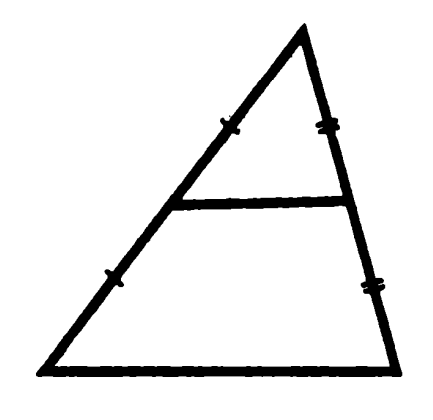
Задача 6. Докажите, что длина отрезка, соединяющего середины двух сторон треугольника, равна половине третьей стороны.
Доказательство: боковые стороны маленького и большого треугольника на рисунке относятся как 1 : 2, кроме того у них есть один общий угол, а значит они подобны по второму признаку с коэффициентом подобия 1 : 2, поэтому и основания относятся как 1 : 2. Что и требовалось доказать.
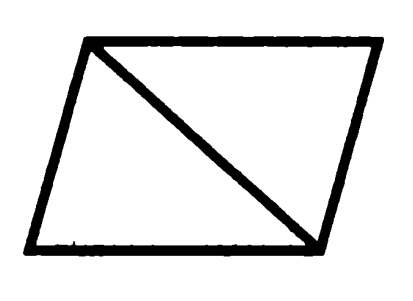
Задача 7. Докажите, что диагональ параллелограмма разбивает его на два равных треугольника.
Доказательство: противоположные стороны параллелограмма равны, диагональ является общей стороной для этих треугольников, поэтому они равны по трем сторонам. Что и требовалось доказать.
Задача 8. Докажите, что медиана, прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство: если вокруг данного прямоугольного треугольника описать окружность, то вписанный в эту окружность прямой угол треугольника будет описаться на полуокружность, поэтому гипотенуза будет диаметром этой окружности, а половинки гипотенузы и данная нам в задаче медиана — радиусами, итак, все они равны. Что и требовалось доказать.
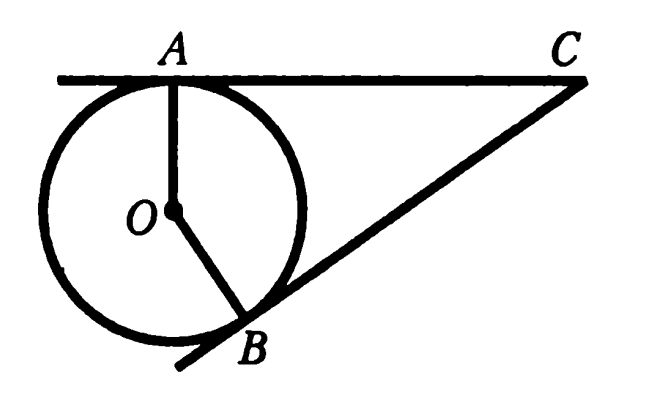
Задача 9. Докажите, что отрезки касательных, проведенных к окружности из одной точки, равны.
Доказательство: углы B и A прямые (радиусы окружности, проведенные в точку качания, перпендикулярны касательным), значит прямоугольные треугольники AOC и BOC равны по гипотенузе (общая для них воображаемая нами сторона OC) и катету (радиусы окружности OB = OA), а значит AC = CB. Что и требовалось доказать.
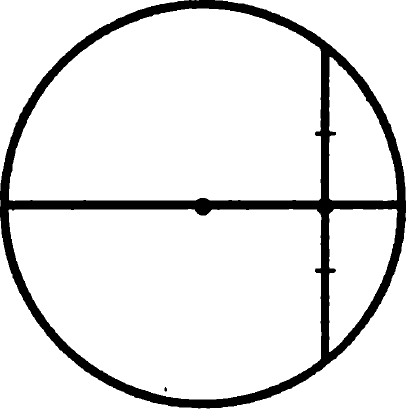
Задача 10. Докажите, что диаметр, проходящий через середину хорды окружности, перпендикулярен ей.
Доказательство: в равнобедренном треугольнике, образованном точками пересечения хорды с окружностью и центром этой окружности, изображенная медиана будет являться высотой, а значит диаметр, содержащий в себе эту высоту, перпендикулярен хорде. Что и требовалось доказать.
Задача 11. Докажите, что если две окружности имеют общую хорду, то прямая, проходящая через центр этих окружностей, перпендикулярна данной хорде.

Мысленно соединяем вместе все отмеченные на рисунке точки, точку пересечения горизонтали и вертикали назовем H
Доказательство: треугольники O1AO2 и O1BO2 равны по трем сторонам, следовательно, ∠HO2A = ∠HO2B, тогда треугольники HAO2 и HBO2 равны по двум сторонам и углу между ними, значит ∠AHO2 = ∠BHO2, а в сумме два равных угла могут давать 1800 только в том случае, если каждый из них равен по 900. Что и требовалось доказать.
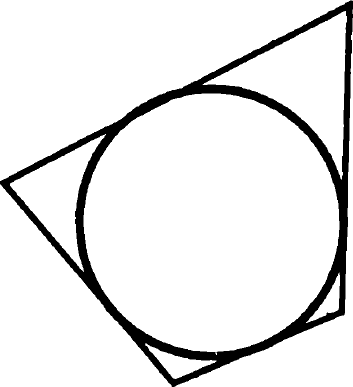
Задача 12. Докажите, что если в четырехугольник можно вписать окружность, то суммы длин его противоположных сторон равны.
Доказательство: используем теорему об отрезках касательных (задача 9). ВК = ВР, СР = СН, DX = DL и АТ = АК. Суммируем стороны АВ и CD: AB + CD = (AM + MB) + (DX + XC) = AL + BE + DL + CE = (AL + LD) + (BE + EC) = AD + BC. Что и требовалось доказать.
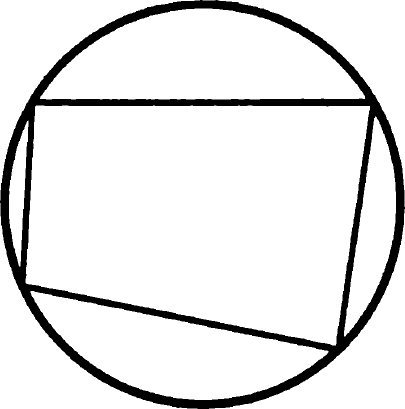
Задача 13. Докажите, что если около четырехугольника можно описать окружность, то суммы его противолежащих углов равны.
Доказательство: по теореме о вписанном угле сумма противолежащих углов этого четырехугольника равна 1800, поскольку вместе они опираются на полную окружность, градусная мера которой 3600. Что и требовалось доказать.
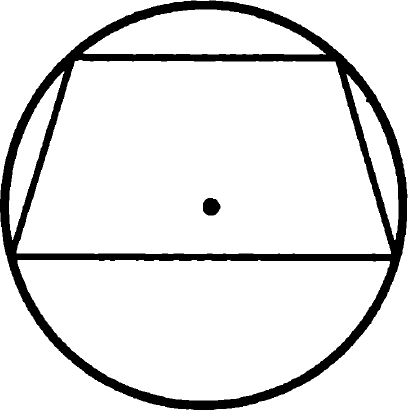
Задача 14. Докажите, что если около трапеции можно описать окружность, то трапеция равнобедренная.
Доказательство: сумма противолежащих углов четырехугольника, вписанного в окружность, равна α + β = 1800 (см. задачу 13), сумма углов при боковой стороне трапеции также равна α + γ = 1800 (эти углы являются односторонними при параллельных основаниях и секущей боковой стороне), из сравнения этих формул получаем, что β = γ, то есть углы при основании такой трапеции равны, и она действительно равнобедренная. Что и требовалось доказать.
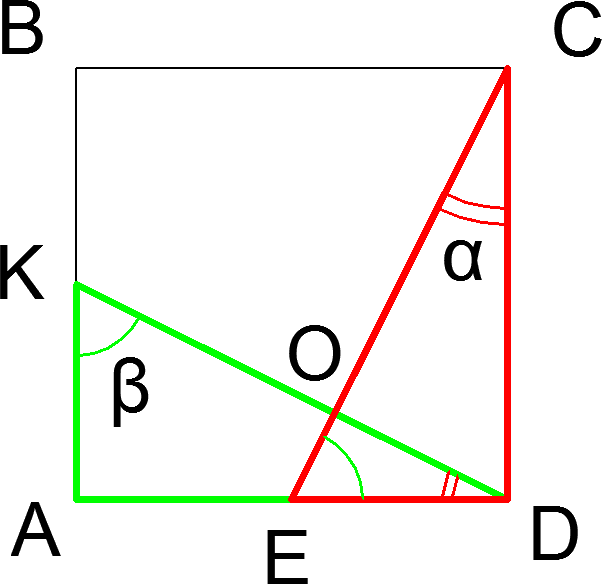
Задача 15. В квадрате ABCD точки К и Е — середины сторон АВ и AD соответственно. Доказать, что КD перпендикулярна CE.
Доказательство. Прямоугольные треугольники AKD и ECD равны по двум катетам, поэтому равны и все их элементы. Пусть ![]()
![]()
Сумма углов в треугольнике равна ![]() Тогда, например, для треугольника AKD имеем
Тогда, например, для треугольника AKD имеем ![]() а значит
а значит ![]() Для треугольника EOD имеем
Для треугольника EOD имеем ![]()
![]() то есть
то есть ![]() а значит
а значит ![]() Что и доказывает перпендикулярность KD и CE.
Что и доказывает перпендикулярность KD и CE.
Доказанные геометрические факты очень важны, их знание будет вам хорошим подспорьем в решении более сложных задач по геометрии, в первую очередь заданий C4 из вариантов ЕГЭ по математике. Изложенные здесь пояснения эталонными решениями, которые нужно приводить на экзамене, конечно, не являются. Это лишь указатели, используя которые, читатель сможет найти решение самостоятельно.
В любом случае умение решать задачи по геометрии является неотъемлемым условием получения высоких баллов на ЕГЭ и ГИА по математике, что будет гарантией поступления во многие престижные вузы. Успехов вам в подготовке к ГИА и ЕГЭ, талантливых наставников и удачи на экзамене! Ваш репетитор по геометрии Сергей Валерьевич.
Понравилась статья? Возможно, это будет вам интересно:


Спасибо! Очень все понятно!
Рад, если это действительно так:-) Однако, если какие-то вопрос все-таки остались, я могу пояснить.
равные хорды AC и BD пересекаются. Докажите , что либо AB=CD либо AD=BC
Ну потому что равные хорды стягивают равные дуги окружности. Тогда за вычетом общей части, оставшиеся части также равны.
дан треугольник ABC в котором AB=7, BC=9, и проведена прямая BD, которая делит треугольник на две части, площади которых относятся как 7:9. докажите что BD- биссектриса угла ABC.
Пусть BD — биссектриса, тогда по свойству биссектрисы треугольника, она делит сторону на отрезки, пропорциональные прилежащим сторонам, то есть AD/AB = DC/BC = 7/9. Треугольники, на которые эта биссектриса разбивает исходный треугольник, имеют одинаковую высоту, обозначим ее h. Тогда S_ABD = 1/2hAD, а S_DBC = 1/2hDC, тогда их отношение S_ABD/S_DBC = 7/9, то есть действительно равно 7:9.
Докажите, что биссектрисы двух соседних углов параллелограмма перпендикулярны.
Сумма двух соседних углов параллелограмма равна альфа+бета=180 градусов, поскольку они является односторонними при параллельных прямых, являющимися его противоположными сторонами. Поскольку это биссектрисы, каждый из углов они делят пополам, поэтому сумма половин этих улов есть альфа/2+бета/2=90 градусов. Тогда в треугольнике, образованном этими биссектрисами и стороной параллелограмма сумма двух углов равна 90 градусов, значит третий угол равен 90 градусов (так как сумма углов в треугольнике 180 градусов). Это и доказывает перпендикулярность.
Если не очень понятно, напишите, добавлю чуть в статью решение с картинкой.
Спасибо огромное! всё понятно.
Здравствуйте! Требуется Ваша помощь!
В квадрате ABCD точки К и Е — середины сторон АВ и AD соответственно. Доказать, что КD перпендикулярна CE.
Хорошая задача, спасибо. Добавил решение в статью, посмотрите (задача 15). Спрашивайте, если что-то непонятно.
Сергей Валерьевич, большое спасибо!
Помогите плз!
«Докажите что треугольник равнобедренный, если медианы, проведенные к его боковым сторонам, равны.»
Заранее спасибо!
Представьте себе или нарисуйте треугольник ABC, в котором медиана CM равна медиане AN, и они пересекаются в точке O. Медианы точкой пересечения делятся в отношении 2:1, считая от вершины. Тогда CO = AO (2/3 каждой медианы), MO = ON (1/3 каждой медианы), угол MOA = углу NOC (вертикальные), значит треугольник MOA = треугольнику NOC (первый признак). Значит, NC = NB = MA = MB, значит AB = BC.
Некоторые моменты я не стал расписывать подробно, если нужно что-то пояснить, спрашивайте.
Здравствуйте,помогите.Надо доказать равенство остроугольных треугольников по двум сторонами и высоте,проведенной к третьей стороне.
Пусть в треугольниках ABC и A1B1C1 AB=A1B1, BC=B1C1 и BH=B1H1 (высоты, проведенные к третьей стороне). Тогда по теореме Пифагора AH = корень (AB^2-BH^2) = корень (A1B1^2-B1H1^2) = A1H1 (заменили равными сторонами). Аналогично HC = H1C1. Но AC = AH+HC = A1H1+H1C1 = A1C1. Получилось, что и третьи стороны тоже равны. Значит эти треугольники равны по трем сторонам.
а можно, как-нибудь по-другому решить, без теоремы Пифагора???
Кажется, что это самый простой способ.
докажите, что средняя линия трапеции равна полусумме ее оснований.
Виктория, это одна из тех теорем, которые изучаются по геометрии в школе, доказательство поэтому можно найти в учебнике. Вот например доказательство из Атанасяна:
http://yourtutor.info/wp-content/uploads/2012/05/teorema-o-srednej-linii-tra.png
В параллелограмме ABCD точка M-середина стороны AB.Известно,что MC=MD.Докажте,что данный параллелограмм-прямоугольник.
Хорошая задача, спасибо. Доказательств этого на самом деле можно придумать несколько. Вот одно из них:
http://yourtutor.info/wp-content/uploads/2012/05/Dokazat-chto-parallelogramm-prjamougolnik.pdf
Попробуйте придумать какое-нибудь другое доказательство.
Спасибо)) Хорошие задачи, подходят для разминки. Прорешала все.)
Это очень хороший результат, поздравляю.)
Доведіть, что трикутник з вершинами М(3;4), Р(7;7), К(4;3), рівнобічний
Квадрат расстояния между двумя точками определяется по формуле: (x1-x2)^2+(y1-y2)^2. Тогда квадрат расстояния между точками M и P равен (7-3)^2+(7-4)^2 = 25, квадрат расстояния между точками P и K равен (7-4)^2+(7-3)^2 = 25. Значит равны и сами расстояния. То есть равны две стороны треугольника, значит он рівнобічний или равнобедренный.
Диагональ AC невыпуклого четырехугольника ABCD разделяет этот четырехугольник на два треугольника, причем AB>BC, AB=AD, BC=CD, а прямые, содержащие диагонали четырехугольника, пересекаются в точке О. Сравните периметры пятиугольников BCODA и DCOBA
Они равны. Стороны АВ, AD, OC входят в оба пятиугольника, поэтому требуется доказать только равенство BС + OD = BO + CD.
По условию BC = CD, то есть остается доказать, что OD = BO. Треугольники АВС и АCD равны по трём сторонам, значит все их соответствующие углы равны. Следовательно, ОА — биссектриса равнобедренного треугольника ABD, а значит и его медиана, то есть OD = BO.
равнобедренная трапеция вписана в окружность радиуса 13,основания равны 10 и 24.найти высоту
Решение задачи (pdf)
Кстати, условие, что трапеция равнобедренная — излишнее, поскольку только вокруг равнобедренной трапеции можно описать окружность.
точка O середина OB стороны AB квадрата ABCD радиус окружности описанной около треугольника AOC равен корень из 10 см вычислите периметр квадрата
«Точка O середина OB стороны AB квадрата ABCD». Какое-то заклинание непонятное. Может быть вот так надо: «Точка O — середина стороны AB квадрата ABCD»?
Здравствуйте! Помогите пожалуйста решить задачу. Докажите, что боковую сторону трапеции, описанной вокруг окружности с центром О, видно с точки О под углом 90 градусов.
Напишу без подробных пояснений. Если будет не понятно, могу расписать подробнее.
Центр вписанной окружности лежит в точке пересечения биссектрис углов. Сумма углов при боковой стороне трапеции равна 180 градусов, а тогда сумма двух углов треугольника, образованного биссектрисами углов и боковой стороной трапеции, равна 180/2 = 90 градусов. Поэтому оставшийся угол также равен 90 градусов.
Помогите с задачей.Отрезки АВ и СД -диаметры окружности.Докажите что хорды ВД и АС равны.
Это следует из равенства треугольников ВДО и АСО, где О — центр окружности. А равны эти треугольники по двум сторонам и углу между ними. AO = OB, CO = OD (радиусы окружности), угол AOC = углу BOD (вертикальные).
Спасибо большое за помощь
помогите пожалуйста)
Отрезки AB и CD пересекаются в точке О , OB =OC и угол B= углу C
Докажите равенство треугольников AOC и DOB
Поскольку OC = OB, то треугольник COB — равнобедренный, поэтому угол OCB = углу OBC, а поскольку угол B= углу C, то угол OBD = углу OCA (две оставшиеся частички равных углов). Кроме этого угол AOC = углу BOD (вертикальные), OB =OC (по условию), следовательно, треугольники AOC и DOB равны по стороне и двум прилежащим к ней углам.
Помогите пожалуйста!
Докажите, что биссектрисы углов трапеции, пересекаясь, образуют четырехугольник, вокруг которого можно описать окружность.
Решение Вашей задачи:
http://yourtutor.info/wp-content/uploads/2012/01/биссектрисы-углов-трапеции-образуют-четырехугольник-вокруг-которого-можно-описать-окружность.pdf
помогите пожалуйста, известно что треугольник АВD и треугольник CFE равнобедренные и имеют только по 2 равных сторон, равны ли они? почему?
Если равны два основания и две боковые стороны данных равнобедренных треугольников, то и две оставшиеся боковые стороны тоже равны, тогда эти треугольники равны по трем сторонам. А вот если две боковые стороны одного равнобедренного треугольника соответственно равны двум боковым сторонам другого треугольника, то равными эти треугольники быть не обязаны, поскольку ничего не сказано о равенстве их оснований. Признака равенства треугольников по двум сторонам нет.
В окружности проведены две параллельные хорды,стягивающие дугу в 90 (гр.) .Длина одной из них 8 см. Найдите длину отрезка диаметра ,заключенного между хордами.
Не могу понять условие, можно подробнее? Каким именно образом две параллельные хорды стягивают дугу 90 градусов? О каком именно диаметре идет речь?
Здравствуйте.
Кажется, у Вас в задаче №2 ошибка, т.к. там сказано отрезки AB и CD пересекаются в точке O, а у Вас пересекаются отрезки AC И BD, Сейчас сама решаю её и не могу.
Задачу 2 доказала, но у Вас, я думаю, все равно опечатка)
Здравствуйте. Да, спасибо большое, опечатку исправил.
Дан равнобедренный треугольник с основанием 4. Рядом с ним окружность, центр вне треугольника, она касается основания и в точке пересечения делит его пополам. Если продлить боковые стороны треугольника, то она их тоже касается. Ее радиус — 2,5. Найти радиус окружности, вписанной в треугольник. Задача часто в ГИА встречается.
Да, действительно, очень часто в ГИА встречается. Подробный видеоразбор задачи: http://egetrener.ru/view_rolik.php?id=443
Помогите пожалуйста! Я не очень хорошо знаю геометрию можете подсказать с чего мне начать заниматься, чтобы результат виден был на лицо? Я уже не знаю что мне делать, руки опускаются.. Спасибо заранее!
Лучше школьного учебника пособия для подготовки не найти. Последовательно, шаг за шагом изучать все темы, решать задачи. Процесс длительный и сложный, но иначе никак. Главное не паниковать, а спокойно готовиться и пользоваться помощью других людей, если есть такая возможность.
Помогите пожалуйста с задачей: докажите, что если две хорды AC и BD пересекаются в точке М, то произведение длин отрезков одной хорды равно произведению длин отрезков другой хорды.
заранее спасибо.
Это теорема об отрезках пересекающихся хорд. Доказательство простое, там все из подобия треугольников следует. Вот доказательство, ребята презентацию делали: http://yourtutor.info/wp-content/uploads/2013/03/otrizki_hord_theorem.png
Помогите пожалуйста! На сторонах параллелограмма внешним образом построены квадраты. Докажите, что четырехугольник с вершинами в центрах этих квадратов является квадратом.
Пусть P,Q и R — центры квадратов, построенных на сторонах DA,AB и BC параллелограмма с острым углом a при вершине A. Легко проверить, что угол PAQ = 90° + a = углу RBQ, а значит, треугольник PAQ = треугольнику RBQ. Стороны AQ и BQ этих треугольников перпендикулярны, поэтому PQ перпендикулярна QR.
Здравствуйте, помогите пожалуйста.
Докажите, что если биссектриса пересекает основание трапеции, то от трапеции отсекается равнобедренный треугольник.
Здравствуйте. Доказываем. Пусть биссектриса BK пересекает бОльшее основание AD трапеции ABCD. Тогда углы AKB и KBC равны как накрест лежащие при параллельных прямых. Кроме этого угол KBC равен углу KBA, так как BK — биссектриса. Следовательно, Угол AKB равен углу ABK, следовательно, треугольник ABK — равнобедренный (у него оказались равны два угла при основании BK).
Добрый день, очень нужна ваша помощь, не могу сама разобраться.
Биссектрисы всех внутренних углов параллелограмма попарно пересекаются. Докажите, что полученный четырехугольник является прямоугольником.
Эту задачу пора поместить в список наиболее часто задаваемых вопросов:-). То, что эти биссектрисы попарно параллельны, доказать не сложно. Действительно, противолежащие углы параллелограмма равны, равны и их половинки, биссектрисы образуют один и тот же угол с параллельными прямыми (противоположными сторонами параллелограмма), поэтому они параллельны.
Далее. Односторонние угла при параллельных прямых в сумме дают 180 градусов. Поскольку биссектрисы делят эти угла пополам, сумма соответствующих половинок равна 90 градусов. Значит на оставшийся угол в треугольнике, образованном пересекающимися биссектрисами и стороной параллелограмма остается 90 градусов.
Помогите пожалуйста!
Диагонали трапеции разбивают ее на 4 треугольника. Докажите, что треугольники, прилежащие к боковым сторонам, равновелики.
Давайте рассмотрим трапецию ABCD с боковыми сторонами AB и CD. Пусть ее диагонали AC и BD пересекаются в точке O. Докажем, что площади треугольников ABO и CDO равны. Начнем с того, что равны площади треугольников ABD и ACD, потому что у них одно общее основание AD и равны высоты, проведенные к этому основанию (эти высоты равны высоте трапеции). Но треугольник AOD — общая часть этих треугольников. Значит площади оставшихся частичек тоже удут одинаковы.
Здравствуйте, нужна ваша помощь.
На стороне ВС квадрата ABCD взята точка К. Докажите, что площадь треугольника AKD равна половине площади квадрата.
Здравствуйте. Площадь треугольника равна половине произведения высоты на основание. Высота в треугольнике AKD, проведенная из вершины K, равна стороне квадрата (обозначим ее за a), основание AD есть сторона квадрата, ее длина также равна a. Тогда площадь треугольника равна 1/2*a*a, а это как раз в два раза меньше площади квадрата, которая равна a*a.
Докажите, что медианы треугольника разбивают его на шесть равновеликих треугольников
Классическая задача. Вот здесь можно решение посмотреть: http://pm298.ru/reshenie/hjtyu.php
Здравствуйте,
Найдите отношение двух сторон треугольника, если его медиана, выходящая из их общей вершины, образует с этими сторонами углы в 30 и 90 градусов.
Пусть ABC — треугольник, CM — медиана, угол MCA = 90, угол BCM = 30. На продолжении медианы CM построим отрезок DM, равный CM. Тогда ABCD — параллелограмм (диагонали точкой пересечения делятся пополам). Тогда треугольник CDB — прямоугольный с прямым углом CDB. В нем против угла в 30 градусов лежит катет DB, равный половине гипотенузы CB. Это и есть искомое отношение. Ответ 2:1.
Докажите, что отрезок соединяющий середины противоположных сторон параллелограмма, параллельны двум другим его сторонам.
Есть такая теорема (признак параллелограмма): если в четырехугольнике две стороны равны и параллельны, то этого четырехугольник – параллелограмм. Подумайте, тут все из этого признака автоматически получается.
ребенок учит геометрию по учебнику «Геометрия» авторы Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г. Позняк, И.И. Юдина. 8 класс. Небольшой эпизод из жизни: На экзамене в билете была задача: Докажите, что если около трапеции можно описать окружность, то трапеция равнобедренная. В учебнике признаки трапеции : трапеция- это 4-хуголник, у которого 2 стороны параллельны, а 2 другие- не параллельны. Второе определение: трапеция равнобедренная, если ее боковые стороны равны.
ЭТО ВСЁ!!!!!!! НО: Нужны определения, которые по непонятной причине отсутствуют в этом учебнике: 1) Сумма углов трапеции, прилежащих к одной боковой стороны, равна 180; 2) свойство трапеции, вокруг которой можно описать окружность- это то, что сумма ее противоположных углов равна 180 градусам……. Как с таким качеством теоретического материала можно научить ребенка решать геометрические задачи???? Это, конечно, не к Вам вопрос… Спасибо за ваш сайт.
надо доказать, что если биссектрисы в треугольниках равны, то и треугольники равны. помогите, пожалуйста.
Нет, это неверное утверждение.
Очень хороший сайт! готовлюсь по нему к сдаче ГИА! Большое спасибо! Просто и понятно.
Какие свойства есть у отрезка, соединяющего точки пересечения биссектрис углов при основании треугольника с боковыми сторонами ? Треугольник произвольный.
Здравствуйте,Сергей! Помогите,пожалуйста,моему ребенку доказать теорему: на боковых сторонах равнобедренного треугольника отложены равные отрезки,есть медиана.Доказать,что отрезки равны.
Здравствуйте, Наталья. Уточните, пожалуйста, равенство каких отрезков требуется доказать?
Здравствуйте!помогите пожалуйста докажите что хорда окружности не проходящая через центр меньше диаметра
Здравствуйте. Длина хорды окружности вычисляется по формуле 2sqrt(R^2-h^2), где R — радиус окружности, h — длина перпендикуляра из центра окружности на хорду. Это меньше 2R.
Спасибо большое
Здравствуй! Помоги поожалуйста, докажите что треугольники при боковых сторонах, образованные диагоналями трапеции равновелики, как то так. 🙂
Спасибо заранее
Пусть есть трапеция ABCD с основаниями AB и CD. Тогда площадь треугольника ABD равна площади треугольника CAB, так как у них общее основание AB и равные высоты (высота трапеции). Значит они равновелики. Ну, соответственно, равновелики и треугольники ADO и COB (O — точка пересечения диагоналей трапеции), так как треугольник AOB — это их общая часть.
Добрый вечер, помоги решить задачу 7 класс задачи на построение
Точка A – одна из точек пересечения двух окружностей с центрами O1 и O2. Проведите через A прямую, которая пересекала бы окружности в точках B и C таким образом, чтобы хорды AB и AC были равны. Спасибо
Здравствуйте, задача уже разбиралась здесь:
http://e-science.sources.ru/node/119116
В трапецию ABCD с основаниями AD и BC вписана окружность с центром в точке О. Докажите, что угол AOB = 90градусов.
Помогите по жалуйста!
Центр вписанной окружности лежит в точке пересечения биссектрис углов A и B. Эти углы в сумме дают 180 градусов (односторонние при параллельных прямых). Значит сумма углов ABO и BAO равна 90 градусов (половина), а значит угол AOB = 90 градусов, т.к. сумма углов в треугольнике равна 180 градусов.
Помоги, пожалуста, сделать построение:
Даны 2 отрезка PQ, ET и угол Н. Постройте четырехугольник ABCD, в котором BO = PQ, OD = ET, угол COD = углу Н и АО*ОС = ВО*OD.
Строим отрезки BO и OD на одной прямой. Через точки B и D проводим окружность. Строим угол COD. Продлеваем сторону CO до пересечения с окружностью в точке A. Четырехугольник ABCD — искомый, так как по теореме о пересекающихся хордах АО*ОС = ВО*OD.
два круга с центрами в точках а и в пересекаются в точках m и n доказать что треугольники nab и mab равны при любых радиусах окружностей помогитеее
Эти треугольники равны по трём сторонам (одной общей, две другие — соответственно равные радиусы окружностей)
Здравствуйте. Ищу, как доказать формулу площади эллипса. Везде пишут доказательство через интеграл. А можно как-нибудь без интеграла?
Спасибо за вопрос. Ответ в видео и на этой странице.
Помогите, пожалуйста. Докажите что если в равнобедренную трапецию можно вписать окружность то высота равна средней линии.
Это неверное утверждение, поэтому доказать его невозможно.
Как доказать что стороны трапеции параллельны???
Во-первых, не все, а только две. Они называются основаниями. Две другие (боковые стороны) не параллельны. Во-вторых, это не нужно доказывать, это определение.
угол1=углу2
ВД=ДС
ДОК-во
Треугольник АВС-равнобедренный
Дано треугольник АВС
ВС=а АС=б. АВ=с
Провели биссектрисы внешних углов при вершинах А и С. Из вершины В опустили перпендикуляри ВМ и ВN. Знайти длинну отрезка МN