Геометрия на ГИА по математике

Геометрия на ГИА по математике представлена в заданиях 8, 14, 20 и 23 (данные на 2012 год). В этой статье мы кратко охарактеризуем уровень сложности этих заданий и разберем примеры конкретных задач, предлагавшихся для решения выпускникам 9-х классов на Государственной (итоговой) аттестации по математике в 2012 году. Для задачи 23 по геометрии представлен видео разбор. Сразу скажу, что на задаче 20, посвященной в ГИА доказательству различных геометрических фактов, мы останавливаться не будет, поскольку этой теме посвящена отдельная обширная статья «Задачи на доказательство геометрических фактов из ГИА», с которой при желании можно ознакомиться отдельно.

Задача 8 по геометрии из ГИА по математике

Самая простая задача по геометрии из ГИА по математике. Однако для ее решения нужно иметь четкое представление об основных понятиях школьного курса геометрии, связанных в первую очередь с темами «Площади», «Подобные треугольники», «Соотношение между сторонами и углами треугольника» и «Длина окружности и площадь круга». При этом как репетитор по математике могу сказать, что одного лишь знания теории этих вопросы совершенно недостаточно для успешного решения задач. Навык решения геометрических задач вырабатывается со временем в процессе систематической и последовательной подготовки под чутким руководством преподавателя.

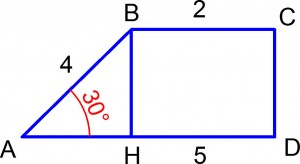
Решение. Подробнее о вычислении площади трапеции читайте в статье «Подробное решение задачи C4 из ЕГЭ по математике». Напомню, что площадь трапеции определяется как произведение полусуммы оснований трапеции (параллельных сторон трапеции) на ее высоту. Подписываем трапецию и проводим в ней высоту:

BH — высота прямоугольной трапеции ABCD

Основаниями данной трапеции являются стороны и Их полусумма (половина суммы) равна Высоту ищем из прямоугольного треугольника для которого по определению синуса острого угла прямоугольного треугольника имеем: то есть

Итак, площадь трапеции равна произведению полусуммы оснований на высоту 2, то есть 7.

Ответ: 7.

Задача для самостоятельного решения №1. Боковая сторона трапеции, образующая с большим основанием угол в 30°, равна 3. Найдите площадь трапеции, если ее основания равны соответственно 2 и 6.

Задача 14 по геометрии из ГИА по математике

Более сложная задача по геометрии из ГИА по математике. В 2012 году составители вариантов ГИА по математике посвятили задачу 14 теореме о вписанном угле.

Рисунок к задаче 14 по геометрии с окружностью из ГИА по математике

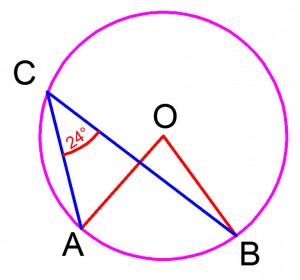
Решение. Угол ACB  — вписанный (его вершина лежит на окружности, а стороны пересекают эту окружность), он опирается на дугу AB. Следовательно, по теореме о вписанном угле градусная мера дуги AB вдвое больше самого угла ACB, то есть равна 24° · 2 = 48°.

Угол AOB — центральный (его вершина лежит в центре окружности), он опирается на ту же дугу AB. По свойству центрального угла его градусная мера равна градусной мере дуги, на которую он опирается, то есть ∠ACB = 48°.

Ответ: 48.

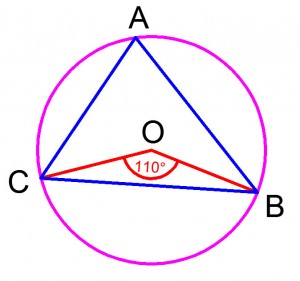
Задача для самостоятельного решения №2. Точка O — центр окружности, ∠BOC = 110° (см. рисунок). Найдите величину угла BAC (в градусах).

Рисунок к задаче 14 по геометрии для самостоятельного решения из ГИА по математике

Хочу отметить, что если в 2012 году составители ГИА предпочли выбрать для задачи 14 тему «Вписанный угол», то это вовсе не означает, что она же будет выбрана для этой задачи и в последующие годы. Напротив, вероятность такого выбора скорее уменьшается. Поэтому как репетитор по математике настоятельно рекомендую ликвидировать все имеющиеся пробелы в курсе геометрии. Без этого условия успешная сдача ГИА по математике не гарантирована.

Задача 23 по геометрии из ГИА по математике

Самая сложная задача по геометрии из предлагаемых на ГИА по математике. Решить ее из года в год оказывается по силам совсем небольшому количеству школьников. И тем не менее научиться решать задачи 23 из ГИА по математике можно и нужно обязательно, хотя бы потому, что подобные задачи ожидают вас и в ЕГЭ по математике, который также придется сдавать всем без исключения выпускникам в 11 классе. Подготовиться к решению сложных задач по геометрии из ГИА по математике проще всего с помощью репетитора.

Пример 3. Стороны AC, AB и BC треугольника ABC равны и соответственно. Точка K расположена вне треугольника ABC, причем отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC > 90°.

Чертеж к задаче 23 по геометрии из ГИА по математике

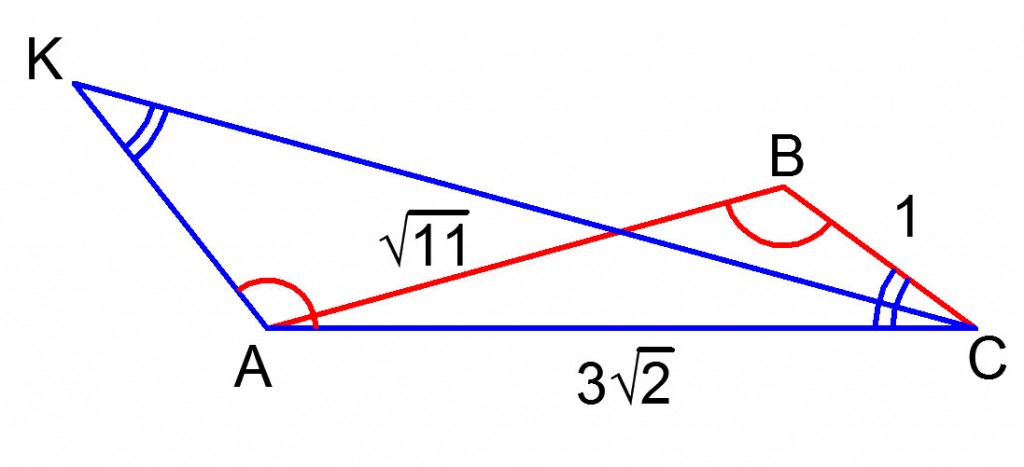
Решение. Угол B в треугольнике ABC тупой. В этом легко убедиться на основании теоремы косинусов (см. видео урок). Известно, что в подобных треугольниках соответствующие углы равны. То есть для каждого угла  одного из подобных треугольников обязательно найдется равный ему угол из второго треугольника. По условию треугольники CKA и ABC подобны. Следовательно, для тупого угла KAC в треугольнике ABC найдется равный ему угол. Это угол B. Больше тупых углов в треугольнике ABC нет, поскольку в треугольнике не может быть больше одного тупого угла. В противном случае сумма всех его углов была бы больше 180º.

Ищем две оставшиеся пары равных углов. Предположим сперва, что угол AKC равен углу BAC, но тогда угол KCA равен углу BCA, что невозможно, так как второй угол больше первого. Следовательно, на самом деле угол AKC равен углу ACB. Находим его косинус по теореме косинусов для треугольника ABC (см. видео урок). Искомый косинус равен

Ответ:

Задача для самостоятельного решения №3. Стороны треугольника равны 10, 10, 12. Найдите радиусы вписанный и вневписанных окружностей.

На сегодня все. Зададимся напоследок вопросом. Зачем вообще нужно изучать геометрию? Не так давно я посетил семинар одного известного российского методиста, посвященный вопросам методики преподавания геометрии в школе. Докладчику в ходе обсуждения среди прочих был задан и этот вопрос. Ответ настолько мне понравился, что я позволю себе привести его здесь почти дословно.

Без полноценного питания невозможно нормальное развитие человека. Без разнообразной интеллектуальной пищи невозможно нормальное интеллектуальной развитие. Сегодня геометрия является одним из немногих качественных продуктов, потребляемых в образовательной сфере. Геометрия — витамин для мозга. Но при этом геометрия — продукт, который должен быть приготовлен очень хорошим кулинаром. Иначе она может не только не принести пользы организму, но и причинить ему вред. Так что учить геометрию нужно с «правильным» репетитором по математике, только он сможет помочь вам достичь успеха в этом нелегком деле. Талантливых вам преподавателей!

Репетитор по математике в Москве (метро Юго-Западная)
Сергей Валерьевич