Поступление в лицей НИУ ВШЭ – это заветная мечта многих школьников и их родителей. Но поступить туда не просто, для этого нужно пройти конкурсный отбор, включающий в себя тестирование по профильным предметам, в том числе по математике. Ко мне, как к репетитору по математике и физике, часто обращаются родители абитуриентов с просьбой помочь подготовиться к тестированию по математике в лицей НИУ ВШЭ. В данной статье представлен разбор варианта вступительного тестирования по математике в лицей ВШЭ. Предложите своему ребёнку выполнить данные задания самостоятельно. Узнайте, вдруг ему тоже требуется помощь профессионального репетитора для подготовки к этому вступительному испытанию.
Разбора заданий вступительного тестирования в лицей при ВШЭ
| 1. Найдите значение выражения
при |
Упростим сперва выражение, находящееся в левых скобках:
![]()
Выражение, стоящее в правых скобках, может быть также преобразовано к виду:
![]()
Тогда после деления результата первого действия на результат второго мы получаем:
![Rendered by QuickLaTeX.com \[ \frac{(2u-v)^2}{u} : \frac{2u-v}{u} = \frac{(2u-v)^2\cdot u}{u\cdot (2u-v)} = 2u-v. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-00e487e6691a11885a8b5dcaeb48b159_l3.png)
Подставляем в полученное выражение данные из условия. В результате получаем:
![]()
![]()
| 2. Вычислите значение выражения:
|
Начнём с упрощения выражения, стоящего в скобках. Как видите, общий знаменатель равен: ![]() . Тогда получается следующее выражение:
. Тогда получается следующее выражение:
![Rendered by QuickLaTeX.com \[ \frac{\sqrt{3}(\sqrt{2}+\sqrt{3})}{\sqrt{6}}-\frac{\sqrt{2}(\sqrt{3}-5)}{\sqrt{6}} = \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-a8d73979b63acae93385aa72b514deb9_l3.png)
![Rendered by QuickLaTeX.com \[ = \frac{\sqrt{6}+3-\sqrt{6}+5\sqrt{2}}{\sqrt{6}} = \frac{3+5\sqrt{2}}{\sqrt{6}}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-26f58b87f75f8d725b25ddd1ae575262_l3.png)
Далее полученные выражение умножаем на дробь, записанную справа от знака умножения:
![Rendered by QuickLaTeX.com \[ \frac{3+5\sqrt{2}}{\sqrt{6}}\cdot \frac{\sqrt{30}}{3+5\sqrt{2}} = \frac{\sqrt{5}\cdot\sqrt{6}}{\sqrt{6}} = \sqrt{5}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-dc028cde5cdb4ab22109a81230bbb5d1_l3.png)
| 3. На сколько процентов надо уменьшить |
Пусть искомое число процентов равно ![]() . Тогда после уменьшения
. Тогда после уменьшения ![]() на
на ![]() процентов останется
процентов останется ![]() . При этом при уменьшении
. При этом при уменьшении ![]() на 52% получится
на 52% получится ![]() . Тогда полученные после этих преобразований число равно:
. Тогда полученные после этих преобразований число равно:
![Rendered by QuickLaTeX.com \[ \frac{0.48x}{\frac{100-n}{100}y}= \frac{48x}{(100-n)y}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f715d5bf82ce7cb603412af8d9559f74_l3.png)
По условию это число составляет 240% от исходного числа ![]() . Следовательно, имеет место уравнение:
. Следовательно, имеет место уравнение:
![]()
Так как понятно, что ![]() , обе части уравнения можно разделить на
, обе части уравнения можно разделить на ![]() . Тогда для
. Тогда для ![]() в результате получаем:
в результате получаем:
![]()
То есть число ![]() было уменьшено на 80%.
было уменьшено на 80%.
| 4. Найдите наибольшее значение функции
|
Представлена квадратичная функция с коэффициентами ![]() ,
, ![]() и
и ![]() . Графиком этой квадратичной функции является парабола. Ветви этой параболы направлены вниз, поскольку коэффициент
. Графиком этой квадратичной функции является парабола. Ветви этой параболы направлены вниз, поскольку коэффициент ![]() .
.
Следовательно, наиболее значение эта функция принимает в вершине соответствующей параболы. Абсцисса вершины параболы вычисляется по формуле:
![Rendered by QuickLaTeX.com \[ x_0=-\frac{b}{2a} = -\frac{6}{2\cdot\left(-\frac{1}{4}\right)} = 12. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-b362fb09c38e7b8d1305f05f0d2e9de1_l3.png)
Тогда легко находится ордината вершины. Она и будет являться наибольшим значением данной функции:
![]()
| 5. Найдите сумму квадратов корней уравнения |
Сперва разделим обе части этого уравнения на 2. Тогда получится следующее уравнение: ![]() . Зачем мы это сделали? Чтобы коэффициент при
. Зачем мы это сделали? Чтобы коэффициент при ![]() стал равен 1.
стал равен 1.
Теперь можно воспользоваться теоремой Виета. Пусть ![]() и
и ![]() — корни данного квадратного уравнения. Тогда имеем:
— корни данного квадратного уравнения. Тогда имеем:
![Rendered by QuickLaTeX.com \[ \begin{cases} x_1+x_2=-41 \\ x_1x_2 = \frac{81}{2}. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f86f2f00555db6452837dabf296370c9_l3.png)
Умножим на 2 обе части второго уравнения, а в первом уравнении обе части возведём в квадрат и раскроем скобки. В результате получаем:
![Rendered by QuickLaTeX.com \[ \begin{cases} x_1^2+2x_1x_2+x_2^2= 1681\\ 2x_1x_2 = 81. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-18fc875a9f6ad937903a81ad67a2c719_l3.png)
Теперь вычтем почленно второе уравнение системы из первого и в результате получим требуемый ответ:
![]()
![]()
| 6, Решите неравенство
|
Начнём с определения области допустимых значений данного неравенства. Известно, что выражение, стоящее в знаменателе дроби, не может быть равно 0, а выражение, стоящее под знаком корня, не может быть отрицательным. Следовательно, область допустимых значений данного неравенства определяется следующим условием: ![]() .
.
Для всех ![]() , удовлетворяющих этому условию, исходное неравенство эквивалентно следующему:
, удовлетворяющих этому условию, исходное неравенство эквивалентно следующему: ![]() . Получается, что исходное сложное неравенство эквивалентно следующей системе неравенств:
. Получается, что исходное сложное неравенство эквивалентно следующей системе неравенств:
![Rendered by QuickLaTeX.com \[ \begin{cases} 3-4x-4x^2> 0\\ 3-10x>0. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-5cdfb7c6f18fec8aa5c3affa7f881825_l3.png)
Решаем первое неравенство системы методом интервалов. Второе неравенство решается элементарным образом. В результате приходим к следующей системе:
![Rendered by QuickLaTeX.com \[ \begin{cases} -\frac{3}{2}<x<\frac{1}{2}\\ x<\frac{3}{10}. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-7fe5c4d7692880fcc7102b6241b66611_l3.png)
Ответом к заданию будет пересечение промежутков, служащих решением каждого из неравенств данной системы. Итак, ответ: ![]() .
.
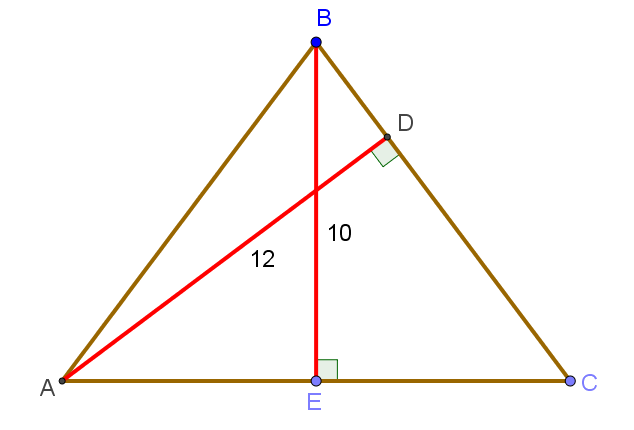
| 7. Найдите площадь равнобедренного треугольника ABC, если высота, опущенная на основание, равна 10, а высота, опущенная на боковую сторону, равна 12. |
Пусть в равнобедренном треугольнике ABC с основанием AC проведена высота BE длиной 10 и высота AD длиной 12:
Введём следующие обозначения. Пусть ![]() и
и ![]() . Известно, что площадь треугольника вычисляется путём умножения длины его высоты на половину длины основания, к которому эта высота проведена. Тогда площадь треугольника ABC с одной стороны равна
. Известно, что площадь треугольника вычисляется путём умножения длины его высоты на половину длины основания, к которому эта высота проведена. Тогда площадь треугольника ABC с одной стороны равна ![]() , а с другой стороны —
, а с другой стороны — ![]() . То есть
. То есть ![]() .
.
Поскольку высота BE проведена в равнобедренном треугольнике ABC к основанию AC, то она является также и медианой этого треугольника. Следовательно, ![]() . Тогда по теореме Пифагора для прямоугольного треугольника BEC получаем:
. Тогда по теореме Пифагора для прямоугольного треугольника BEC получаем:
![Rendered by QuickLaTeX.com \[ 10^2+\left(\frac{b}{2}\right)^2 = a^2\Leftrightarrow 400 + b^2 = 4a^2. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-bb64555b48470f4674a81a351ef2192c_l3.png)
С учётом найденной ранее связи между ![]() и
и ![]() получаем:
получаем:
![Rendered by QuickLaTeX.com \[ 400 + b^2 = 4\times\left(\frac{5}{6}b\right)^2\Rightarrow b = 15. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e61163a1b8b21bca7fd9fee91c58b224_l3.png)
Тогда искомая площадь треугольника равна 75.
| 8. Если в арифметической прогрессии |
Пусть разность данной арифметической прогрессии равна ![]() . Обращаем сразу внимание на то, что третий член арифметической прогрессии получается вычитанием удвоенной разности этой прогрессии из пятого её члена. В cвою очередь, седьмой член арифметической прогрессии получается добавлением удвоенной разности этой прогрессии к пятому её члену.
. Обращаем сразу внимание на то, что третий член арифметической прогрессии получается вычитанием удвоенной разности этой прогрессии из пятого её члена. В cвою очередь, седьмой член арифметической прогрессии получается добавлением удвоенной разности этой прогрессии к пятому её члену.
Аналогично, девятый член арифметической прогрессии получается вычитанием удвоенной разности этой прогрессии из одиннадцатого её члена. А тринадцатый член арифметической прогрессии получается добавлением удвоенной разности этой прогрессии к одиннадцатому её члену.
С учётом этих обстоятельств получаем:
![]()
![]()
| 9. Из пункта А в пункт В выехал велосипедист, который приедет в В через 2 часа, одновременно с ним из В в А вышел пешеход, который придет в А через 6 часов. Через какое время они встретятся? |
Здесь в варианте вступительного тестирования по математике в лицей ВШЭ предлагается решить задачу на движение. Пусть скорость пешехода равна ![]() . Тогда скорость велосипедиста равна
. Тогда скорость велосипедиста равна ![]() , ведь он движется в 3 раза быстрее пешехода. Тогда скорость сближения велосипедиста и пешехода равна
, ведь он движется в 3 раза быстрее пешехода. Тогда скорость сближения велосипедиста и пешехода равна ![]() , что в 4 раза больше скорости пешехода. Значит, в сумме они преодолеют расстояние от A к В (то есть встретятся), спустя промежуток времени, который в четыре раза меньше того времени, которое требуется пешеходу, чтобы дойти из пункта A в пункт B. То есть через
, что в 4 раза больше скорости пешехода. Значит, в сумме они преодолеют расстояние от A к В (то есть встретятся), спустя промежуток времени, который в четыре раза меньше того времени, которое требуется пешеходу, чтобы дойти из пункта A в пункт B. То есть через ![]() часа.
часа.
| 10. Взяли 5 листов бумаги, один из них разрезали на 5 частей, один из полученных снова на 5 и так далее. Какое число листов можно таким образом получить? 2015, 2016, 2017 или 2018? |
Если записать в ряд количество листков, которые получаются в результате всех этих действий на каждой итерации, то получится арифметическая прогрессия с разностью 4. Значит, может получиться только число, которое при уменьшении на 5 делилось бы нацело на 4. Из всех предложенных это число 2017.
Задание с полным решением из вступительного экзамена в лицей НИУ ВШЭ
Дано уравнение ![]() .
.
а) Найдите наименьшее целое значение параметра ![]() , при котором уравнение имеет корни разных знаков.
, при котором уравнение имеет корни разных знаков.
Начнём с того, что параметр ![]() , в противном случае уравнение имело бы только один корень. Разделим обе части уравнения на
, в противном случае уравнение имело бы только один корень. Разделим обе части уравнения на ![]() . В результате приходим у следующему уравнению:
. В результате приходим у следующему уравнению:
![]()
Как узнать при каких значениях ![]() корни этого уравнения будут различны по знаку? Нужно вспомнить, что графиком соответствующей квадратичной функции является парабола, ветви которой направлены вверх. Причём эта парабола пересекает вертикальную ось в точке с ординатой
корни этого уравнения будут различны по знаку? Нужно вспомнить, что графиком соответствующей квадратичной функции является парабола, ветви которой направлены вверх. Причём эта парабола пересекает вертикальную ось в точке с ординатой ![]() . Следовательно, корни будут различны по знаку, если свободный член отрицателен. То есть имеет место неравенство:
. Следовательно, корни будут различны по знаку, если свободный член отрицателен. То есть имеет место неравенство:
![]()
Итак, наименьшее целое значение из полученного промежутка — это число -3.
б) Найдите длину промежутка, в который может попасть значение параметра ![]() , чтобы уравнение имело хотя бы один корень.
, чтобы уравнение имело хотя бы один корень.
Полученное нами уравнение имеет два корня в том случае, если его дискриминант положителен, то есть выполнено неравенство:
![Rendered by QuickLaTeX.com \[ \left(-\frac{3}{p+4}\right)^2-\frac{4p}{p+4}>0\Leftrightarrow \frac{9-4p(p+4)}{(p+4)^2}>0. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-93555dc991fd522e4544678ded5a22b2_l3.png)
Последнее неравенство выполняется при ![]() .
.
Один корень будет, когда дискриминант равен нулю, то есть при ![]() и
и ![]() , а также при
, а также при ![]() , поскольку в этом случае уравнение становится линейным.
, поскольку в этом случае уравнение становится линейным.
Из всего вышесказанного заключаем, что промежуток, в который может попасть значение параметра ![]() , чтобы уравнение имело хотя бы один корень, — это промежуток
, чтобы уравнение имело хотя бы один корень, — это промежуток ![]() . Длина этого промежутка равна
. Длина этого промежутка равна ![]() .
.
в) Найдите сумму всех значений ![]() , при которых уравнение имеет ровно 1 корень.
, при которых уравнение имеет ровно 1 корень.
Корень будет один, если ![]() , и когда дискриминант равен 0, то есть при
, и когда дискриминант равен 0, то есть при ![]() и
и ![]() . Тогда искомая сумма равна -8.
. Тогда искомая сумма равна -8.
Телефон репетитора для подготовки к вступительному тестированию по математике в лицей НИУ ВШЭ, Сергея Валерьевича
Сайт для подготовки к вступительному тесту по математике в лицей ВШЭ
Понравилась статья? Возможно, вам будет интересна также следующая:


![Rendered by QuickLaTeX.com \[ \left(4u-4v+\frac{v^2}{u}\right):\left(2-\frac{v}{u}\right) \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-09acb1b617e05cf3520a5f0a1ddba5ac_l3.png)
![Rendered by QuickLaTeX.com \[ \left(\frac{\sqrt{2}+\sqrt{3}}{\sqrt{2}}-\frac{\sqrt{3}-5}{\sqrt{3}}\right)\cdot\frac{\sqrt{30}}{3+5\sqrt{2}}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e3ba2ce2e06351c38bdab4698d6db976_l3.png)
Здравствуйте, Сергей Валерьевич.
Какие задания предлагаются при поступлении в 8 класс?
Спасибо.
С уважением
Борис Григорьевич.
Здравствуйте, Борис Григорьевич. Демонстрационные варианты Вы можете на официальном сайте лицея или на сайте https://cleverfox.info/
стоимость занятия с Вами?
Здравствуйте,а для поступления в какой класс эти задания?
Здравствуйте, в 10
Сергей, посоветуйте тренировочные варианты для поступления в 9 класс?
Разбор одного варианта (демонстрационного) на этом сайте недавно выложен на этой странице.
Множество тренировочных вариантов с подробными решениями всех заданий выложены на моём сайте https://cleverfox.info/
В 7 задаче вместо ED=1/2b надо EC=1/2b. Еще много ошибок. Исправите эту — напишу остальные.
Спасибо, исправил эту опечатку.
а что у них есть 8 класс? я только с 9 вижу
Они набирают только в 9 и 10 классы. По крайней мере, на данный момент. Иногда ещё дополнительные наборы в 11 класс устраивают на освободившиеся места.