Университетская гимназия МГУ — это молодое, но уже крайне востребованное образовательное учреждение Москвы. Ежегодно оно ведёт набор абитуриентов со всей страны. И желающих по-настоящему очень много. Конкурс из года в год очень высокий. Подготовиться к вступительным экзаменам не просто. Лучше всего заниматься для этого с профессиональным репетитором, специализирующимся на подготовке к вступительным экзаменам именно в эту гимназию и имеющим большое количество учеников, которые успешно справились с конкурсным отбором и стали счастливыми учащимися Университетской гимназии МГУ.
Я давно об этом говорю и я искренне рад, что со мной согласны в самой гимназии, о чём они недавно напрямую написали на своём сайте. Действительно, именно занятия с профессиональным репетитором являются самым эффективным способом подготовки, что подтверждается историческим опытом. Однако, не всегда есть возможность нанять репетитора. В этом случае нужно пытаться подготовиться самостоятельно. К сожалению, на сайте гимназии в настоящий момент отсутствуют примеры заданий, которые дают на вступительных экзаменах. Поскольку я, как репетитор для подготовки к поступлению в гимназию МГУ, на протяжении нескольких лет успешно занимаюсь этим делом, то за эти годы у меня накопилось много вариантов вступительных экзаменов, которые предлагались абитуриентам в разные годы.
В помощь тем, кто готовится к поступлению в гимназию МГУ, я запускаю новый цикл материалов на Youtube, а также на специальном канале в телеграмме (https://t.me/msu_gymn), посвящённый разбору демонстрационных и реальных вступительных экзаменов в гимназию МГУ прошлых лет. Это уникальная возможность для самостоятельной подготовки к экзамену по математике. Так что подписывайтесь на этот канал, а также на мой новый канал в Телеграмме, чтобы не пропускать все важные и полезные выпуски.
А начнём мы с разбора демонстрационного вступительного экзамена по математике за 2021 год, который предлагался для следующих профилей: история, филология и право. В Телеграмм-канале уже выложен сам вариант и решение некоторых заданий. А в этой статье мы разберём весь вариант целиком. Итак, приступим.
Разбор демоварианта 2021 года по математике для профилей: история, филология, право
Задание 1. Найдите значение выражения
![]()
при ![]() и
и ![]() .
.
Решение. Упрощаем выражение в скобках:
![]()
![]()
Выполняем деление:
![]()
![]()
Задание 2. Решите систему уравнений:
![Rendered by QuickLaTeX.com \[ \begin{cases} 2x^2+3y^2=11, \\ 4x^2+6y^2=11x \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-837ed3cb9c4d356e89d26e305d008602_l3.png)
Решение. Умножим первое уравнение в системе на 2:
![Rendered by QuickLaTeX.com \[ \begin{cases} 4x^2+6y^2=2, \\ 4x^2+6y^2=11x \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-6c51e7a521e58a2f74d2c351dcc1cf09_l3.png)
Так как выражения слева от знаков равенства в обоих уравнениях теперь одинаковые, то равны и выражения, стоящие справа от знаков неравенства. То есть ![]() , откуда
, откуда ![]() .
.
Подставляем теперь полученное значение ![]() в первое уравнение исходной системы и получаем:
в первое уравнение исходной системы и получаем:
![]()
![]()
![]()
Итак, решениями системы являются две точки: ![]() и
и ![]() .
.
Задание 3. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 130 литров она заполняет на 4 минуты быстрее, чем первая труба заполняет резервуар объёмом 136 литров?
Решение. Пусть вторая труба пропускает ![]() литров воды в минуту. Тогда первая труба пропускает
литров воды в минуту. Тогда первая труба пропускает ![]() литра воды в минуту. Значит, первой трубе потребуется
литра воды в минуту. Значит, первой трубе потребуется ![]() минуты, чтобы заполнить резервуар объёмом 136 литров, а второй трубе потребуется
минуты, чтобы заполнить резервуар объёмом 136 литров, а второй трубе потребуется ![]() минут, чтобы заполнить резервуар объёмом 130 литров. Так как время второй трубы на 4 минуты меньше, чем время первой, то имеет место уравнение:
минут, чтобы заполнить резервуар объёмом 130 литров. Так как время второй трубы на 4 минуты меньше, чем время первой, то имеет место уравнение:
![]()
![]()
![]()
![]()
![]()
Второй корень ![]() , поэтому не подходит по смыслу условия задачи.
, поэтому не подходит по смыслу условия задачи.
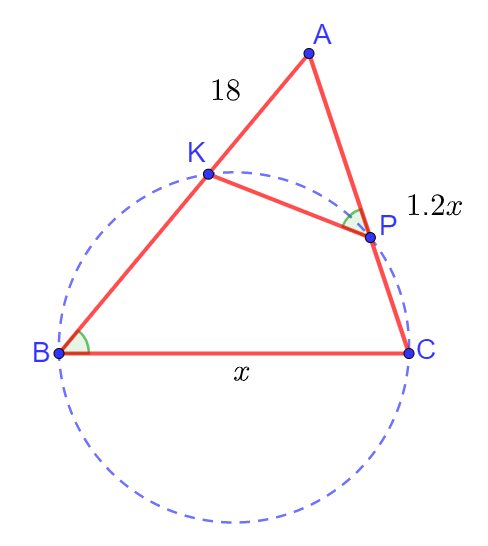
Задание 4. Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 18, а сторона AC в 1.2 раза больше стороны BC.
Решение. Изобразим ситуацию на рисунке:
Заметим сразу, что ![]() , так как четырёхугольник BCPK является вписанным в окружность. Кроме того,
, так как четырёхугольник BCPK является вписанным в окружность. Кроме того, ![]() , так как эти углы являются смежными. Из этих двух равенств следует, что
, так как эти углы являются смежными. Из этих двух равенств следует, что ![]() .
.
Рассмотрим треугольники AKP и ABC. У них есть общий угол A, а также пара равных углов APK и ABC, поэтому эти треугольники подобны. То есть имеет соотношение:
![]()
![]()
![]()
Ответ: 15.
Задание 5. Алик, Миша и Вася покупали блокноты и трёхкопеечные карандаши. Алик купил 2 блокнота и 4 карандаша, Миша — блокнот и 6 карандашей, Вася — блокнот и 3 карандаша. Оказалось, что суммы, которые уплатили Алик, Миша и Вася, образуют геометрическую прогрессию. Сколько стоит блокнот?
Решение. Пусть блокнот стоит ![]() копеек. Тогда Алик заплатил
копеек. Тогда Алик заплатил ![]() копеек, Миша заплатил
копеек, Миша заплатил ![]() копеек, Вася заплатил
копеек, Вася заплатил ![]() копеек. Так как суммы, которые уплатили Алик, Миша и Вася образуют геометрическую прогрессию, то верно равенство:
копеек. Так как суммы, которые уплатили Алик, Миша и Вася образуют геометрическую прогрессию, то верно равенство:
![]()
![]()
![]()
У полученного уравнения есть только один положительный корень 18.
Ответ: 18 копеек.
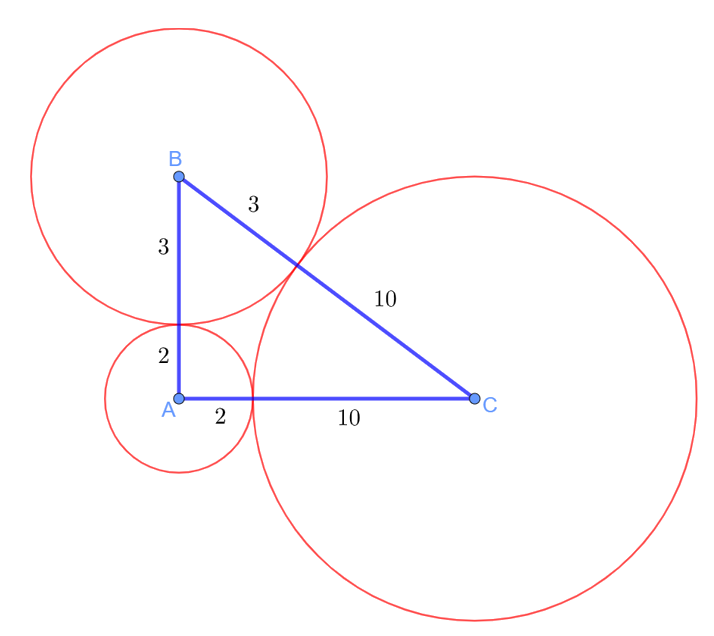
Задание 6. Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трёх окружностей.
Решение. Изобразим ситуацию на рисунке:
Стороны получившегося треугольника ABC равны ![]() ,
, ![]() и
и ![]() . Поскольку
. Поскольку ![]() , то по теореме обратной теореме Пифагора получаем, что этот треугольник прямоугольный.
, то по теореме обратной теореме Пифагора получаем, что этот треугольник прямоугольный.
Итак, задача свелась к нахождению радиуса вписанной окружности в прямоугольный треугольник с известными сторонами:
Для этого используем, что площадь треугольника равна произведению его полупериметра на радиус вписанной окружности: ![]() . Имеем:
. Имеем:
![]()
![]()
![]()
Ответ: 2.
Это был разбор демонстрационного варианта вступительного экзамена в Университетскую гимназию МГУ для профилей: история, филология и право. Если вам требуется подготовка к вступительному экзамену в гимназию МГУ, обращайтесь ко мне. Как репетитор по математике и физике, я имею большой опыт такой подготовки. Многие мои ученики успешно прошли конкурсный отбор и стали счастливыми учениками этой замечательной гимназии. Так что звоните или пишите. Мои контакты вы найдёте на этой странице.
Ну а также подписывайтесь на мой новый телеграмм-канал, посвящённый подготовке к вступительным экзаменам в гимназию МГУ: https://t.me/msu_gymn. Там выкладываются полезные материалы, а также варианты вступительных экзаменов прошлых лет с решениями, по которым вы сможете самостоятельно готовиться к поступлению.
Успехов вам в этой непростом, но очень правильном начинании! Материал подготовил репетитор для подготовки к поступлению в гимназию МГУ Сергей Валерьевич.



Добавить комментарий