Комплексный тест по математике в лицей ВШЭ

Автор

Среда, 2 августа, 2017

Вывеска лицея ВШЭВ статье представлен разбор заданий из первой и второй части демонстрационного варианта вступительного комплексного теста по математике в лицей ВШЭ. Решения всех заданий составлены профессиональным репетитором по математике и физике, который занимается подготовкой школьников к поступлению в лицей ВШЭ по математике и физике.

Разбор первой части комплексного теста по математике в лицей ВШЭ

1. Вычислите:

    \[ \left((0,75)^2:\frac{18}{7}+\frac{1}{3}\right)\cdot 72. \]

  1. 5,3
  2. 39,75
  3. 6
  4. 0,24

    \[ \left(\left(\frac{3}{4}\right)^2\cdot\frac{7}{18}+\frac{1}{3}\right)\cdot 72=\left(\frac{9}{16}\cdot\frac{7}{18}+\frac{1}{3}\right)\cdot 72= \]

    \[ =\left(\frac{7}{32}+\frac{1}{3}\right)\cdot 72 = \frac{53}{96}\cdot 72 = \frac{159}{4}=39,75. \]

Правильный ответ: 2.

2. Пятиметровое бревно нужно распилить на метровые поленья. Распиловка бревна поперёк отнимает каждый раз полторы минуты. Сколько минут потребуется, чтобы распилить всё бревно?

  1. 4,5 мин
  2. 6 мин
  3. 7,5 мин
  4. 5,5 мин

Потребуется 4 распила. Поскольку каждый распил длится 1,5 минуты, то общее время, которое потребуется, равно 6 минутам.

Правильный ответ: 2.

3. На сколько процентов надо повысить цену, чтобы после 20% скидки товар стоил столько же, сколько и первоначально?

  1. 25
  2. 15
  3. 20
  4. 30

Пусть изначально товар стоил x. Тогда после 20% скидки он стал стоить 0,8x. Чтобы стоимость товара стала равна исходной, цену вновь нужно поднять на 0,2x. Это составляет

    \[ \frac{0,2x}{0,8x}\cdot 100\% = 25\% \]

от текущей стоимости. Итак, цену нужно повысить на 25%.

Правильный ответ: 1.

4. Найдите наименьшее целое решение неравенства (2-\sqrt{5})x<2+\sqrt{5}.

  1. -17
  2. -18
  3. 17
  4. -16

Разделим обе части неравенства на отрицательное число 2-\sqrt{5}, знак неравенства при этом изменится:

    \[ x>\frac{2+\sqrt{5}}{2-\sqrt{5}}. \]

Упростим выражение, стоящее справа. Для этого умножим числитель и знаменатель на выражение, сопряжённое со знаменателем. В результате получаем следующее выражение:

    \[ \frac{(2+\sqrt{5})^2}{(2-\sqrt{5})(2+\sqrt{5})} = -9-4\sqrt{5}. \]

Итак, окончательно неравенство принимает вид:

    \[ x>-9-4\sqrt{5}. \]

Легко убедиться, что

    \[ 2,23<\sqrt{5}<2,24. \]

Учитывая это, получаем

    \[ -17,96<-9-4\sqrt{5}<-17,92. \]

То есть нужно найти ближайшее целое число, которое больше -17,92. Это число -17. Оно и будет являться наименьшим целым решением исходного неравенства.

Правильный ответ: 1.

5. Набор матрёшек, состоящий из восьми штук, поставили в ряд по высоте от меньшей к большей. Известно, что высота третьей матрёшки равна шести сантиметрам. Каждая следующая матрёшка на две целых и три десятых сантиметра больше предыдущей. Какой высоты будет восьмая матрёшка?

  1. 41,5
  2. 19,8
  3. 15,5
  4. 17,5

Перед нами арифметическая прогрессия. Пусть высота первой матрёшки равна a_1, тогда известно, что a_3=6. Кроме того, известна разность этой прогрессии d=2,3. Тогда, используя формулу n-ого члена арифметической прогрессии, находим a_1:

    \[ a_3=a_1+2d \Leftrightarrow a_1=6-2·2,3 = 1,4. \]

Теперь находим a_8:

    \[ a_8=a_1+7d=1,4+7·2,3=17,5. \]

Правильный ответ: 4.

6. Трёх людей по подозрению в контрабанде ловят таможенники и устраивают допрос. Первый и второй задержанные говорят: «Я не виноват!». Третий задержанный говорит: «Второй — контрабандист!» Известно, что правду говорит только один из них. Кто из задержанных контрабандист?

  1. Первый
  2. Второй
  3. Третий
  4. Невозможно определить

Предположим, что правду говорит третий. Тогда второй — контрабандист. Но тогда правду говорит и первый, который говорит, что он не виноват. А это противоречит условию, что правду говорит только один человек.

Предположим теперь, что правду говорит первый. Тогда при этом третий врёт, что второй — контрабандист. Значит, контрабандист — третий. Но тогда второй, говоря, что он не виноват, говорит правду. А это вновь противоречит условию, что правду говорит только один человек из трёх.

Осталось предположить, что правду говорит второй. При этом первый врёт, что он не контрабандист. Значит, он как раз и есть контрабандист. При этом врёт и третий, говоря, что контрабандист — второй. Это единственная ситуация, возникающая без противоречия условию.

Итак, контрабандист — первый.

Правильный ответ: 1.

7. В прямоугольном треугольнике катеты равны 5 и 12. Чему равен синус большего острого угла треугольника?

  1. 5/13
  2. 12/13
  3. 1
  4. 5/12

Пусть a=5 и b=12 — катеты данного прямоугольника, а c — его гипотенуза. Сперва по теореме Пифагора находим гипотенузу этого прямоугольного треугольника:

    \[ c=\sqrt{a^2+b^2}=\sqrt{5^2+12^2} = 13. \]

Больший острый угол лежит в этом треугольнике против большего катета. То есть синус большего острого угла \alpha равен отношению большего катета b к гипотенузе c:

    \[ \sin\alpha = \frac{b}{c} = \frac{12}{13}. \]

Правильный ответ: 2.

8. Если первое (1) и второе (2) высказывания являются верными, то верно ли третье (3) высказывание или четвёртое (4) высказывание?

(1) Если у меня в корзинке лежит овощ овальной формы, то он зелёный.

(2) Если у меня в корзинке лежит огурец, то он зелёный.

(3) Если у меня в корзинке лежит овощ овальной формы, то он огурец.

(4) Если овощ зелёный, то он овальный.

  1. Верное третье
  2. Верно четвёртое
  3. Неверно третье и четвёртое
  4. Невозможно дать ответ

Третье неверно, так как из (1) и (2) не следует, что не может быть других зелёных овощей овальной формы, кроме огурцов. Четвёртое также неверное, так как из (1) не следует, что нет зелёных овощей не овальной формы.

Правильный ответ: 3.

9. Когда автомобиль проехал 10 км и ещё 3/4 оставшегося пути, ему осталось проехать 1/6 всего пути и ещё 10 км. Какова длина пути?

  1. 180 км
  2. 300 км
  3. 150 км
  4. 120 км

Пусть длина пути равна x км, тогда в соответствии с условием имеет место следующее уравнение:

    \[ x=10+\frac{3}{4}(x-10)+\frac{1}{6}x+10. \]

Из этого уравнения находим x=150 км.

Правильный ответ: 3.

10. Решите уравнение

    \[ \frac{x+6}{6-x}+\frac{x-6}{x+6}=\frac{6}{36-x^2}. \]

  1. 0,25
  2. 3
  3. -1/4
  4. -0,5

Переносим все члены уравнения в левую сторону от знака равенства и приводим всё к общему знаменателю:

    \[ \frac{(x+6)^2-(6-x)^2-6}{(6-x)(6+x)}=0. \]

После всех преобразований в числителе уравнение принимает вид:

    \[ \frac{-24x+6}{(x+6)(x-6)}=0. \]

Для x\ne\pm 6 уравнение равносильно уравнению -24x+6=0. Решая последнее уравнение, получаем x=\frac{1}{4}=0,25.

Правильный ответ: 1.

Разбор второй части комплексного теста по математике в лицей ВШЭ

1. Найдите все значения x, для каждого из которых имеет смысл выражение:

    \[ \frac{\sqrt{(2x-4)(3-2x-x^2)}}{4x-5}. \]

Множество всех значений x, для каждого из которых имеет смысл записанное выражение, задаётся системой неравенств:

    \[ \begin{cases} (2x-4)(3-2x-x^2)\geqslant 0 \\ 4x-5\ne 0. \end{cases} \]

Решаем первое неравенство с помощью метода интервалов. Для этого разложим на множители вторую скобку:

    \[ 3-2x-x^2 = (x+3)(1-x). \]

Решением неравенства

    \[ (x-2)(x+3)(1-x)\geqslant 0 \]

является множество всех x\in[-\mathcal{1};-3]\cup[1;2].

Из второго неравенства получаем. что x\ne 1,25. Это число нужно исключить из окончательного ответа. В результате получаем ответ:

    \[ x\in[-\mathcal{1};-3]\cup[1;1,25)\cup(1,25;2]. \]

2. Найдите все значения b такие, что система уравнений

    \[ \begin{cases} 18x+3y=3b, \\ 6x+by=1 \end{cases} \]

имеет единственное решение. Решить графически систему при одном из возможных значений b.

Во втором уравнении выражаем x через y:

    \[ x=\frac{1-by}{6}. \]

Подставляем теперь x в первое уравнение системы:

    \[ 18\cdot\frac{1-by}{6}+3y=3b\Leftrightarrow \]

    \[ 3-3by+3y-3b=0\Leftrightarrow \]

    \[ 1-by+y-b=0. \]

Методом группировки раскладываем выражение слева от знака равенства на множители и получаем в результате:

    \[ (1-b)(1+y)=0. \]

Возможны два варианта:

1) При b=1 уравнение имеет бесконечное количество корней, так как y может быть любым числом. При этом исходная система также имеет бесконечное количество решений, удовлетворяющих условию x=\frac{1-y}{6}.

2) При b\ne 1 уравнение имеет единственное решение y=-1. Значит, исходная система уравнений при этом также имеет единственное решение \left(\frac{1+b}{6};-1\right).

Итак, при b\ne 1 система имеет единственное решение.

Для примера возьмём b=5. Графическое решение системы в этом случае представлено на рисунке:

Графическое решение системы уравнений из комплексного тест по математике в лицей ВШЭ

Видно, что система имеет в этом случае единственное решение (1;-1).

3. Настя, Катя, Ира и Оля учредили компанию с уставным капиталом 300 000 рублей. Настя внесла 17% уставного капитала, Катя — 48 000 рублей, Ира — 0,14 уставного капитала, а остальную часть уставного капитала внесла Оля. Учредители договорились делить ежегодную прибыль пропорционально внесённому в уставной капитал вкладу. Сколько рублей от прибыли в 500 000 рублей причитается Оле?

1. Ира и Настя вместе внесли 31% уставного капитала, то есть:

300 000×0,31 = 93 000 рублей.

2. Так как Катя внесла 48 000 рублей, то Оля внесла оставшуюся часть в 159 000 рублей. Это составляет:

159 000÷300 000×100% = 53% от уставного капитала.

3. На этот же процент от прибыли может рассчитывать Оля. В рублях это составляет:

500 000×0,53 = 265 000.

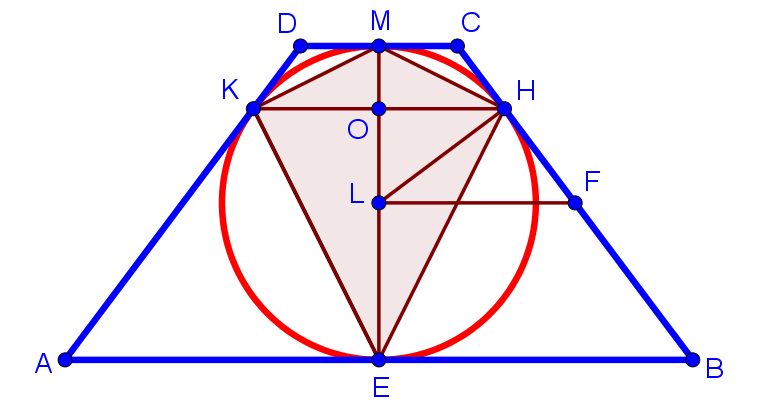
4. Около окружности радиуса 1 описана равнобедренная трапеция. Площадь трапеции равна 5. Найдите площадь четырёхугольника, вершинами которого служат точки касания окружности и трапеции.

Рисунок к геометрической задаче из комплексного теста по математике в лицей ВШЭ

Задача несложная, но доказательств много. Хотя все они довольно очевидны, для полноты решения их нужно расписать. Далее всё будет расписано максимальное подробно для удобства читателя.

  1. Так как трапеция равнобедренная, то вписанная в эту трапецию окружность касается оснований в их серединах. Действительно, DL и CL — биссектрисы равных углов D и C, то есть треугольник DLC — равнобедренный, и высота этого треугольника LM (радиус, проведённый в точку касания перпендикулярен касательной) является медианой. То есть DM = MC. Аналогично, AE = EB.
  2. То есть EM — это отрезок, соединяющий середины оснований равнобедренной трапеции. Докажем, что он перпендикулярен основаниям. Действительно, рассмотрим треугольник DEC. Докажем, что он равнобедренный. Действительно, треугольники ADE и ECB равны по двум сторонам (AD = CB и AE = EB) и углу между ними (∠A = ∠B). Значит, DE = CE. То есть EM — это медиана равнобедренного треугольника DEC, а значит и его высота. То есть EM перпендикулярен DC, поэтому перпендикулярен и AB, так как DC параллелен AB. То есть EM — высота данной трапеции. То есть EM = 2 (два радиуса вписанной окружности).
  3. DK = DM = MC = CH (отрезки касательных) и ∠D = ∠C, поэтому ΔKDM = ΔMCH. Значит, KM = MH. Аналогично доказывается, что KE = EH. Значит, ΔKME = ΔMHE по трём сторонам. Значит, ∠KME = ∠EMH. То есть MO — биссектриса равнобедренного треугольника KMH, проведённая к его основанию. Значит, она является и высотой. То есть ME перпендикулярен KH. То есть в четырёхугольнике EKMH диагонали взаимно перпендикулярны. Значит, его площадь равна половине произведения диагоналей. Осталось найти длину KH.
  4. Так как в трапецию вписана окружность, то суммы её противоположных сторон равны. То есть AB + DC = AD + CB = p, где p — полупериметр. Площадь описанной около окружности трапеции S равна произведению её полупериметра на радиус вписанной окружности r: S = pr. По условию S = 5, а r = 1. Значит, p = 5. LF — половина средней линии трапеции, поэтому LF = AB + DC/4 = p/4 = 5/4.
  5. ∠OHL = ∠HLF (т.к. это накрест лежащие углы при параллельных прямых OH, LF и секущей LH), ∠LHF = ∠HOL = 90°. Значит, треугольники LHF и OLH подобны по двум углам. Из этого подобия получаем, что LF:LH = LH:OH, откуда OH = 4/5. То есть KH = 8/5. Значит, искомая площадь равна ME·KH/2 = 8/5.
5. Найдите все значения параметра a такие, что уравнение (a-1)x^4-\sqrt{2}x^2+a=0 имеет два различных корня.

При a\ne 1 это уравнение является биквадратным. Оно может иметь от 0 до 4 различных корней. Причём задача сформулирована таким образом, что мы ищем значения a такие, что уравнение имеет два различных корня. Не «ровно два», а «просто два» различных корня. То есть, допустим, если уравнение имеет 4 корня, и все они различны, то этот случай нам тоже подойдет, потому что среди них есть два различных.

Преобразуем уравнение. Введём замену t=x^2. Тогда уравнение принимает вид: (a-1)t^2-\sqrt{2}t+a=0. Или для a\ne 1:

(1)   \begin{equation*} t^2-\frac{\sqrt{2}}{a-1}t+\frac{a}{a-1}=0. \end{equation*}

Ищем сперва все значения параметра, при которых у исходного уравнения будет ровна два различных корня.

Эта ситуация реализуется в следующих случаях:

1) когда a=1, так как в этом случае исходное биквадратное уравнение превращается в квадратное -\sqrt{2}x^2+1=0, у которого два различных корня x=\pm\frac{1}{\sqrt[4]{2}}.

2) когда у уравнения (1) есть лишь один положительный корень. Это возможно тогда, когда его дискриминант равен нулю:

    \[ \left(\frac{\sqrt{2}}{a-1}\right)^2-\frac{4a}{a-1}=0. \]

Из последнего уравнения получаем a_1=\frac{1+\sqrt{3}}{2} и a_2=\frac{1-\sqrt{3}}{2}.

Для a_1 соответствующий корень уравнения будет равен:

    \[ t_0=\frac{\sqrt{2}}{2\left(\frac{1+\sqrt{3}}{2}-1\right)} = \frac{\sqrt{2}}{\sqrt{3}-1}>0. \]

Этот случай подходит.

Для a_2 соответствующий корень уравнения будет равен:

    \[ t_0=\frac{\sqrt{2}}{2\left(\frac{1-\sqrt{3}}{2}-1\right)} = \frac{\sqrt{2}}{-1-\sqrt{3}}<0. \]

Этот случай не подходит.

3) когда уравнение (1) имеет корни разных знаков. Эта ситуация реализуется тогда, когда свободный член уравнения (1) отрицателен (соответствующая парабола пересекает ось OY в точке, лежащей ниже оси OX):

    \[ \frac{a}{a-1}<0. \]

Это неравенство решается методом интервалов. Решение задаётся промежутком a\in(0;1).

Итак, объединяя все полученные решения в этом пункте, мы находим все значения параметра a, при каждом из которых исходное уравнение имеет ровна два различных корня: a\in(0;1]\cup\left\{\frac{1+\sqrt{3}}{2}\right\}. Если бы в условии была соответствующая оговорка, мы бы закончили решение и радовались жизни. Но поскольку этой оговорки нет, мы продолжаем.

Ищем теперь все значения параметра, при каждом из которых исходное уравнение имеет ровно три различных корня.

Это возможно только в том случае, если уравнение (1) имеет один положительный корень и один нулевой корень. То есть свободный член уравнения (1) должен быть равен нулю, а вершина параболы должна находиться правее оси OY. То есть имеет место неравенство:

    \[ \begin{cases} \frac{a}{a-1}=0 \\ \frac{\sqrt{2}}{2(a-1)}>0. \end{cases} \]

Однако, не существует ни одного значения параметра a, которое бы удовлетворяло данной системе. То есть трёх корней у исходного уравнения не будет ни при каких значениях параметра a.

И, наконец, ищем все значения параметра, при которых у исходного уравнения будет четыре различных корня.

Здесь уже не обязательно уточнять, используя формулировку «ровно четыре корня», так как биквадратное уравнение имеет не более четырёх корней. Четыре корня у исходного уравнения будет в том случае, если уравнение (1) имеет два различных положительных корня. То есть, когда свободный член положителен (соответствующая парабола пересекает ось OY выше нуля), вершина параболы находится правее оси OY, и дискриминант положителен. То есть имеет место следующая система неравенств:

    \[ \begin{cases} \frac{a}{a-1}>0 \\ \frac{\sqrt{2}}{2(a-1)}>0 \\ \left(\frac{\sqrt{2}}{a-1}\right)^2-\frac{4a}{a-1}>0. \end{cases} \]

Решением этой системы является промежуток a\in\left(1;\frac{1+\sqrt{3}}{2}\right).

Итак, объединяя все решения полученные в каждом из пунктов, получаем ответ к заданию: a\in\left(0;\frac{1+\sqrt{3}}{2}\right].

Примечание. Ещё раз повторюсь, что если бы в условии было чётко указано, что мы ищем все значения параметра a, при которых у исходного уравнения ровно два различных корня, то ответ был бы следующим: a\in(0;1]\cup\left\{\frac{1+\sqrt{3}}{2}\right\}.

Подготовка к комплексному тесту по математике в лицей ВШЭ

Разбор заданий демонстрационного варианта комплексного теста в лицей ВШЭ подставлен профессиональным репетитором по математике в Москве, имеющим обширный опыт подготовки школьников к поступлению в лицей ВШЭ и другие лицей и гимназии Москвы. Если у вас остались какие-либо вопросы, задавайте их в комментариях или обращайтесь напрямую к репетитору. Контактную информацию вы можете найти на этой странице. Также вы можете воспользоваться сайтом cleverfox.info, на котором выложены типовые варианты комплексных тестов по математике в лицей ВШЭ с подробными решениями всех заданий.

Понравилась статья? Возможно, вам будет интересна также следующая:

Метки: , , ,
Опубликовано в категории Методическая копилка | 4 комментария »

Комментарии

  1. Аноним:
    07.09.2018 в 11:11

    пример 3: правильны ответ при неправильном подходе

    Ответить
    1. Сергей:
      07.09.2018 в 15:43

      Почему, на ваш взгляд, этот подход является неправильным?

      Ответить
  2. Ульяна:
    06.02.2019 в 22:14

    Сергей, сделаете ли Вы разбор заданий второй части вступительного теста по математике за 2019 год?

    Ответить
    1. Сергей:
      07.02.2019 в 12:34

      Не успеваю(( С утра до вечера подготовка к занятиям и их проведение. Нужны помощники)) Было бы сейчас лето, когда занятий по минимуму, тогда обязательно сделал бы разбор. А сейчас самая жаркая пора…

      Ответить

Добавить комментарий