В статье представлен разбор задания 15 из ЕГЭ по математике профильного уровня. Для вашего удобства представлен также видеоразбор решения этого задания с подробными комментариями от репетитора по математике.
Статьи с метками ‘подготовка к ЕГЭ по математике с репетитором’
В задании 13 ЕГЭ по математике профильного уровня требуется решить уравнение и осуществить отбор его корней, удовлетворяющих некоторому условию. В данной статье представлен разбор такого задания из профильного уровня ЕГЭ по математике, предложенного в 2016 году. Доступен видеоразбор решения от репетитора по математике.
В задании 14 ЕГЭ по математике выпускникам, сдающим экзамен, необходимо решить задачу по стереометрии. Именно поэтому научиться решать такие задачи должен каждый школьник, если он хочет получить положительную оценку на экзамене. В данной статье представлен разбор двух типов заданий 14 из ЕГЭ по математике 2016 года (профильный уровень) от репетитора по математике в Москве.
Читать дальше »
В задании 18 профильного уровня ЕГЭ по математике школьникам предлагается решить задачу с параметром. Такие задания надо уметь решать. К сожалению, решению именно этого класса задач в школе уделяется очень мало внимания. В данной статье репетитором по математике представлен подробный разбор двух типов заданий 18 профильного ЕГЭ по математике, которые были предложены на экзамене в 2016 году. Имеется видеоразбор решений.
Читать дальше »
В данной статье репетитором по математике и физике дается информация о том, как найти величину вписанного угла. Рассматривается определение вписанного угла, а также теорема о вписанном угле и следствия из этой теоремы. После этого дается подробный анализ решения задачи со вписанным углом.
На днях увидел сие творение в одном из сборников заданий для подготовки к ЕГЭ по математике 2015 года. В этом году авторы-составители решили дополнить КИМы ещё одним нововведением, так называемой «экономической» задачей. Сейчас она числится в вариантах профильного ЕГЭ по математике под №19. Спешу поделиться с вами впечатлениями о ней, дорогие мои читатели.
Довольно часто среди заданий B11 встречаются такие, где требуется определить, к примеру, во сколько раз изменится объем или площадь боковой поверхности какой-нибудь объемной фигуры при изменении ее линейных размеров в известное число раз. Если такая задача попадётся вам на ЕГЭ по математике — радуйтесь, дорогие старшеклассники, вам повезло! Эти задачи решаются устно, буквально в одно действие. В данной статье описан простой способ решения подобных задач B11. Ключом к решению станет для вас одно очень простое правило.
 Разберем сегодня такую задачу C6.
Разберем сегодня такую задачу C6.
Условие
Дана последовательность натуральных чисел, причем каждый следующий ее член отличается от предыдущего либо на 10, либо в 6 раз. Сумма всех членов последовательности равна 257.
а) Какое наименьшее (минимальное) число членов может быть в данной последовательности?
б) Какое наибольшее (максимальное) количество членов может быть в этой последовательности?
На самом деле задачи C6 из ЕГЭ по математике не так уж и сложны, хотя позиционируются они как олимпиадные. Даже если вас пугают нестандартные формулировки, и вы боитесь решать задачи, которые не решали на уроках математики в школе, не паникуйте на экзамене. Попробуйте немного порассуждать, и вы увидите, что не так уж все сложно. Давайте посмотрим, как эта задача очень легко решается.
Читать дальше »
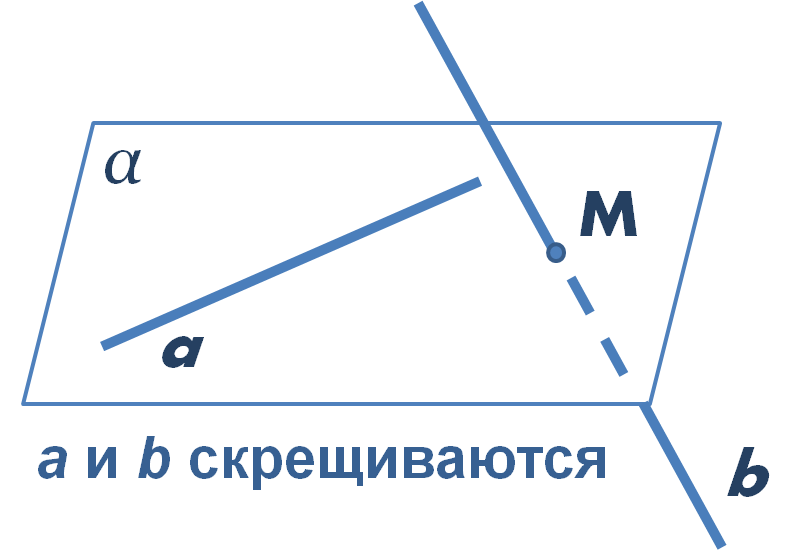
В данной статье на примере решения задачи C2 из ЕГЭ разобран способ нахождения расстояния между скрещивающимися прямыми с помощью метода координат. Напомним, что прямые являются скрещивающи-мися, если они не лежат в одной плоскости. В частности, если одна прямая лежит в плоскости, а вторая прямая пересекает эту плоскость в точке, которая не лежит на первой прямой, то такие прямые являются скрещивающимися (см. рисунок).
Читать дальше »
Для решения задач по геометрии, связанных с треугольниками, важно усвоить одну простую, но важную истину. Существует третий признак равенства треугольников («по трем сторонам»), из которого следует, что не существует двух различных треугольников с одинаковыми сторонами. Следовательно, зная длины всех сторон треугольника, можно узнать об этом треугольнике все, что нужно. В том числе длины его медиан, биссектрис и высот. Разберем более подробно, каким образом это можно сделать.