Разбор задания 15 из ЕГЭ по математике

Автор

Пятница, 15 июля, 2016

В статье представлен разбор задания 15 из ЕГЭ по математике профильного уровня. Для вашего удобства представлен также видеоразбор решения этого задания с подробными комментариями от репетитора по математике.

Решите неравенство:

    \[ \frac{49^x-6\cdot 7^x+3}{7^x-5}+\frac{6\cdot 7^x-39}{7^x-7}\leqslant 7^x+5. \]


Заметим, что 49^x = \left(7^x\right)^2. Введём замену t=7^x>0. Тогда неравенство примет вид:

    \[ \frac{t^2-6t+3}{t-5}+\frac{6t-39}{t-7}\leqslant t+5. \]

Переносим всё члены в левую сторону относительно знака неравенства, приводим всё к общему знаменателю, раскрываем скобки и приводим подобные слагаемые. В результате чего получаем следующее неравенство:

    \[ \frac{t-1}{(t-5)(t-7)}\leqslant 0. \]

Решаем его с помощью метода интервалов:

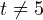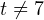  1. Определяем область допустимых значений (ОДЗ) выражения, стоящего слева от знака неравенства. В эту область входят все числа, но t\ne 5 и t\ne 7, поскольку при данных значениях t знаменатель обращается в нуль.
  2. Определяем значения t, при которых выражение равно нулю. Дробь равна нулю, когда нулю равен её числитель, а знаменатель не равен нулю. То есть это одно единственное значение: t=1.
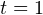  3. Наносим полученные значения, а также значения, которые не входят в ОДЗ, на числовую прямую. После этого определяем знаки выражения в каждом из полученных промежутков на числовой прямой и выбираем те, на которых выражение меньше или равно нулю:

Интервалы на числовой прямой из задания 15 ЕГЭ по математике профильного уровня

    \[ \left[ \begin{array}{l} 0 < t\leqslant 1 \\ 5 < t < 7. \end{array} \]

Далее переходим к обратной подстановке:

    \[ \left[ \begin{array}{l} 0 < 7^x\leqslant 1 \\ 5< 7^x < 7. \end{array} \]

Разбираемся сперва с первым двойным неравенством данной совокупности. Условие 7^x>0 выполняется при любых значениях x, так как показательная функция y=7^x всегда положительна (её график изображён на рисунке снизу). Кроме того, эта функция является возрастающей (большие значения x соответствуют большим значениям y) и равна 1 при x=0. То есть при меньших значениях x функция будет меньше 1. Итак, решением первого двойного неравенства совокупности является промежуток: x\in (-\mathcal{1};0].

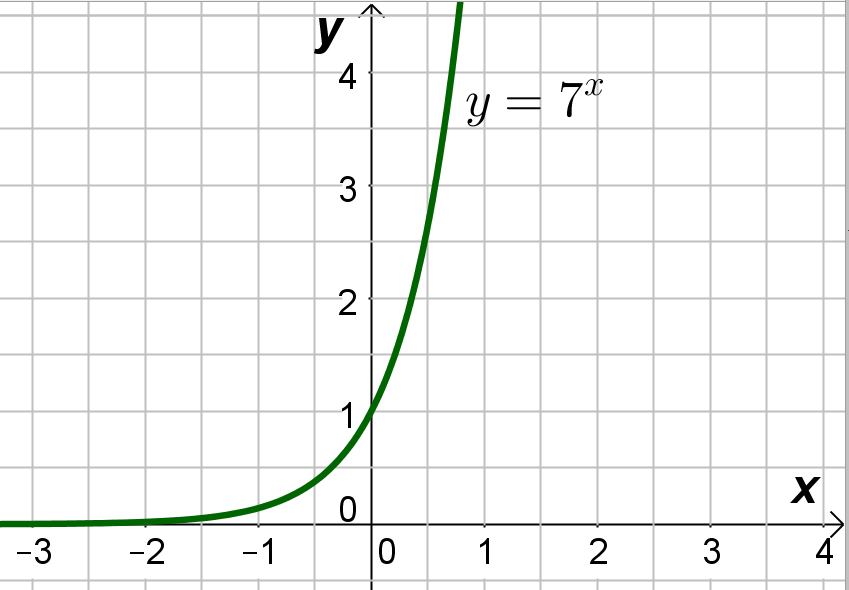
График экспоненты для задания 15 из ЕГЭ по математике

Для решения второго двойного неравенства совокупности также используем свойство возрастания функции y=7^x. В силу возрастания этой функции, чтобы узнать, при каких значениях её аргумента значения функции находятся в промежутке (5;7), достаточно узнать, при каких значениях аргумента x_1 и x_2 значения функции равны 5 и 7. Тогда решение двойного неравенства будет иметь вид: (x_1;x_2). Итак, 7^{x_1}=5, откуда x_1=\log_7 5, и 7^{x_2}=7, откуда x_2=1. То есть решение данного двойного неравенства имеет вид: (\log_7 5;1).

Окончательный ответ: x\in(-\mathcal{1};0]\cup(\log_7 5;1).

Материал подготовлен репетитором по математике в Москве, Сергеем Валерьевичем

 

Метки: , ,
Опубликовано в категории Методическая копилка | 2 комментария »

Комментарии

  1. Герман:
    06.08.2016 в 19:49

    «…раскрываем скобки и подобные слагаемые». Слово «приводим» пропущено, очевидно.

    Ответить
    1. Сергей:
      06.08.2016 в 19:50

      Да, спасибо, исправил.

      Ответить

Добавить комментарий