Разбор профильного ЕГЭ по математике, часть 2, задания 9-12

Пятница, 29 июля, 2016

В данной статье представлен разбор заданий 9-12 части 2 ЕГЭ по математике профильного уровня от репетитора по математике и физике. Видеоурок репетитора с разбором предложенных заданий содержит подробные и понятные комментарии по каждому из них. Если вы только начали подготовку к ЕГЭ по математике, данная статья может оказаться для вас очень полезной.

9. Найдите значение выражения

$\frac{\log_8 20}{\log_8 5}+\log_5 0,05.$

Используя свойства логарифмов, с которыми вы можете подробно ознакомиться в данной статье или в предлагаемом выше видеоуроке, преобразуем выражение:

$\frac{\log_8 20}{\log_8 5}+\log_5 0,05=\log_5 20 +\log_5\left(5\cdot 10^{-2}\right) =$

$=\log_5\left(2^2\cdot 5\right)+\log_5 5 -2\cdot\log_5 \left(2\cdot 5\right) =$

$=2\log_5 2 + \log_5 5 +\log_5 5 -2\log_5 2 -2\log_5 5 = 0.$

10. Пружинный маятник совершает колебания с периодом T = 16 с. Масса подвешенного груза m = 0,8 кг. Скорость движения груза изменяется с течение времени в соответствии с формулой $\upsilon = \upsilon_0\sin\frac{2\pi t}{T}$ . При этом $\upsilon_0 = 0.5$ м/с. Определяющая формула кинетической энергии (в джоулях) имеет вид: $E_K = \frac{m\upsilon^2}{2}$ , где m берётся в килограммах, $\upsilon$ — в метрах в секунду. Чему в джоулях равна кинетическая энергия груза через 10 с после начала колебательного движения?

Скорость движения груза через 10 с после начала колебательного движения будет равна:

$\upsilon = 0.5\cdot\sin\frac{2\pi\cdot 10}{16} = 0.5\cdot \sin\frac{5\pi}{4} = -\frac{\sqrt{2}}{4}$ м/с.

Тогда кинетическая энергия в этот момент времени будет равна:

$E_K=\frac{0.8}{2}\cdot \left(-\frac{\sqrt{2}}{4}\right)^2 = 0.05$ Дж.

11. Известно, что 6 леденцов стоят дешевле шоколадки на 2%. На сколько процентов 9 таких леденцов стоят дороже шоколадки?

Пусть x — цена одного леденца, а y — цена шоколадки. Тогда 6 леденцов стоят 6x, а 2% от стоимости шоколадки равны 0,02y. Поскольку известно, что 6 леденцов стоят дешевле шоколадки на 2%, то имеет место первое уравнение: 6x + 0,02y = y, из которого получаем, что x = 0,98/6 y = 98/600 y = 49/300 y. В свою очередь 9 леденцов стоят 9x, то есть 9·49/300 y = 49/300 y = 1,47 y. Задача сводится к тому, чтобы определить на сколько процентов 1,47y больше, чем y. Если y составляет 100%, то 1,47y составляет 1,47·100% = 147%. То есть 1,47y большем, чем y на 47%.

12. Найдите точку минимума функции $y=2x-\ln(x+8)^2$ .

Используем алгоритм нахождения точек экстремума (минимума и максимума) функции:

1) ОДЗ задаётся неравенством: $(x+8)^2>0$ (так выражение, стоящее под знаком логарифма, должно быть больше нуля), откуда получаем, что $x\ne -8$ .

2) Ищем производную функции. Подробный рассказ о том, как вычисляется производная данной функции, смотрите в видео выше. Производная функции равна:

$y'=2-\frac{\left((x+8)^2\right)'}{(x+8)^2} = 2-\frac{2}{x+8} = \frac{2x+14}{x+8}.$

3) Ищем значения x, при которых производная равна 0 или не существует. Она не существует при $x=-8$ , так как в этом случае знаменатель обращается в нуль. Производная обнуляется, когда:

$\frac{2x+14}{x+8} = 0.$

Последняя дробь равна 0 при $x=-7$ .

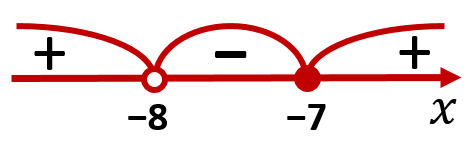
4) Наносим на числовую прямую ОДЗ, точки в которых производная не существует, а также точки, в которых она равна нулю. Далее определяем, какова по знаку производная (положительная или отрицательная) на каждом из полученных промежутков:

Как видно, производная меняет свой знак с отрицательного на положительный в точке $x = -7$ . Значит это и есть точка минимума.

Материал подготовил репетитор по математике и физике, Сергей Валерьевич

Разбор профильного ЕГЭ по математике, часть 2, задания 9-12

Добавить комментарий Cancel reply

Страницы

Понравился сайт?

Последние записи

Архив записей

Прочее