Стереометрии в экзаменационных вариантах ЕГЭ по математике посвящены задачи B9 и C2, первые попроще, вторые посложнее. О некоторых методах решения задач C2 можно почитать в статье «Как решать задачи C2 ЕГЭ по математике — советы репетитора». В данной статье мы подробно остановимся на решении задач B9. Причем как репетитор по физике и математике постараюсь построить изложение таким образом, что через решение простых заданий B9 мы будем переходить к решению более сложных задач C2 по стереометрии из ЕГЭ, связанных с теми же пространственными фигурами и величинами. Как всегда материал будем разбирать на конкретных примерах из вариантов ЕГЭ по математике прошлых лет.
Задачи по стереометрии из ЕГЭ, связанные с параллелепипедом
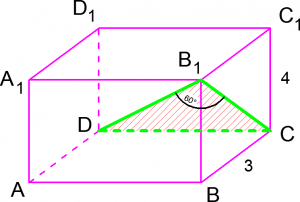
Решение. Так как ![]() — параллелепипед, то
— параллелепипед, то ![]() а значит и любой прямой, лежащей в этой плоскости, в том числе и
а значит и любой прямой, лежащей в этой плоскости, в том числе и ![]() То есть треугольник
То есть треугольник ![]() — прямоугольный, гипотенузой в нем будет являться искомая диагональ
— прямоугольный, гипотенузой в нем будет являться искомая диагональ ![]()
Из прямоугольного треугольника ![]() находим гипотенузу
находим гипотенузу![]() Для прямоугольного треугольника
Для прямоугольного треугольника ![]() имеем
имеем ![]() то есть
то есть ![]()
Ответ: 10.
Задача для самостоятельного решения №1. Диагональ прямоугольного параллелепипеда равна ![]() и наклонена к плоскости его грани под углом
и наклонена к плоскости его грани под углом ![]() Найдите ребро параллелепипеда, перпендикулярное плоскости этой грани.
Найдите ребро параллелепипеда, перпендикулярное плоскости этой грани.
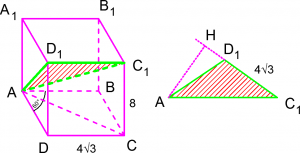
Решение. Искомое расстояние есть высота треугольника ![]() проведенная из вершины
проведенная из вершины ![]() Ищем стороны данного треугольника. Ребро
Ищем стороны данного треугольника. Ребро ![]() Из прямоугольного треугольника
Из прямоугольного треугольника ![]() находим
находим ![]()
Далее ![]() Из теоремы косинусов для треугольника
Из теоремы косинусов для треугольника ![]() получаем, что
получаем, что ![]()
![]() откуда
откуда ![]() Из прямоугольного треугольника
Из прямоугольного треугольника ![]() находим
находим ![]()
Из теоремы косинусов для треугольника ![]() получаем, что
получаем, что ![]() откуда
откуда ![]() Тогда
Тогда ![]() Площадь треугольника равна
Площадь треугольника равна ![]() С другой стороны
С другой стороны ![]() Следовательно,
Следовательно, ![]()
Здесь мы воспользовались приемом сведения задачи по стереометрии из ЕГЭ к задаче по планиметрии. Как видите, в данном случае такой способ решения нельзя назвать наиболее рациональным. И все же он не лишен права на существование. Подробнее о решении планиметрических задач из ЕГЭ по математике читайте в статье «Решение задач C4».
Ответ: 10.
Задача для самостоятельного решения №2. Основанием прямой призмы ![]() является равнобедренный треугольник
является равнобедренный треугольник ![]() боковая сторона которого равна
боковая сторона которого равна ![]() а угол
а угол ![]() равен
равен ![]() Найдите расстояние от точки
Найдите расстояние от точки ![]() до прямой
до прямой ![]() если известно, что боковое ребро данной призмы равно 12.
если известно, что боковое ребро данной призмы равно 12.
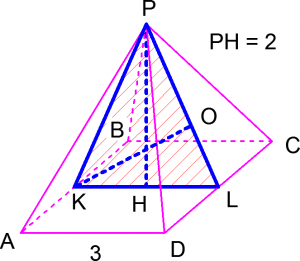
Задачи по стереометрии из ЕГЭ, связанные с пирамидой
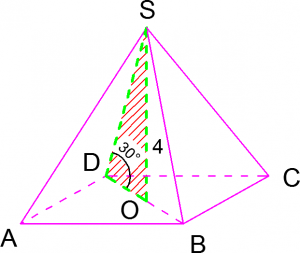
Решение. Угол наклона бокового ребра к плоскости основания есть угол между этим боковым ребром и его проекцией на плоскость основания, то есть угол ![]() где
где ![]() — перпендикуляр из вершины
— перпендикуляр из вершины ![]() на плоскость
на плоскость ![]() (высота пирамиды). Для прямоугольного треугольника
(высота пирамиды). Для прямоугольного треугольника ![]() имеем
имеем ![]() откуда
откуда ![]()
Задача для самостоятельного решения №3. Диагональ основания правильной четырехугольной пирамиды равна 6. Боковое ребро равно 5. Найдите высоту пирамиды.
Показать ответРешение. ![]() лежит в плоскости
лежит в плоскости ![]()
![]() в этой плоскости не лежит и параллельна
в этой плоскости не лежит и параллельна ![]() следовательно,
следовательно, ![]() параллельна
параллельна ![]() Ищем расстояние из точки
Ищем расстояние из точки ![]() (середины
(середины ![]() ), оно будет равно искомому расстоянию из точки
), оно будет равно искомому расстоянию из точки ![]() что следует из доказанного выше.
что следует из доказанного выше.
Точка ![]() находится в центре основания
находится в центре основания ![]() поскольку пирамида правильная. То есть
поскольку пирамида правильная. То есть ![]() Из прямоугольного треугольника
Из прямоугольного треугольника ![]() находим
находим ![]() Площадь треугольника
Площадь треугольника ![]() с одной стороны есть
с одной стороны есть ![]() а с другой стороны
а с другой стороны ![]() Сравнивая полученные результаты, получаем, что
Сравнивая полученные результаты, получаем, что ![]()
Ответ: ![]()
Задача для самостоятельного решения №4. В правильной четырехугольной пирамиде ![]() все ребра которой равны
все ребра которой равны ![]() найдите расстояние между прямыми
найдите расстояние между прямыми ![]() и
и ![]()
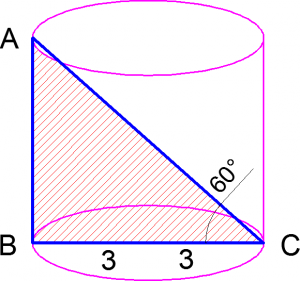
Задачи по стереометрии из ЕГЭ, связанные c цилиндром
Решение. Искомую диагональ ищем из прямоугольного треугольника ![]() По определению косинуса получаем:
По определению косинуса получаем: ![]() откуда находим
откуда находим ![]()
Ответ: ![]()
Задача для самостоятельного решения №5. Образующая цилиндра равна ![]() Диагональ осевого сечения наклонена к плоскости основания цилиндра под углом
Диагональ осевого сечения наклонена к плоскости основания цилиндра под углом ![]() Найдите радиус основания цилиндра.
Найдите радиус основания цилиндра.
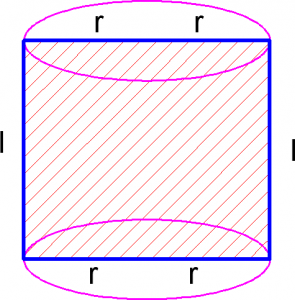
Решение. Из рисунка видно, что периметр осевого сечения цилиндра определяется по формуле: ![]() или, что тоже самое,
или, что тоже самое, ![]() Площадь осевого сечения равна
Площадь осевого сечения равна ![]() с учетом
с учетом ![]() получаем
получаем ![]()
Полученное выражение представляет собой квадратичную функцию ![]() от переменной
от переменной ![]() . Наибольшее значение она принимает в вершине соответствующей параболы, то есть в точке
. Наибольшее значение она принимает в вершине соответствующей параболы, то есть в точке ![]() При этом образующая цилиндра равна
При этом образующая цилиндра равна ![]()
Ответ: ![]() или
или ![]()
Задача для самостоятельного решения №6. Площадь боковой поверхности цилиндра равна площади круга, описанного около его осевого сечения. Найдите отношение радиуса цилиндра к его высоте.
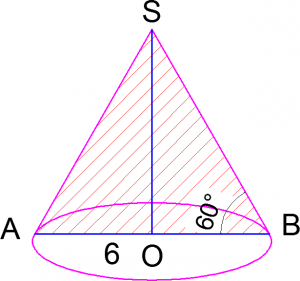
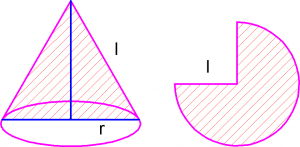
Показать ответЗадачи по стереометрии из ЕГЭ, связанные с конусом
Решение. На рисунке треугольник ![]() — равносторонний, поэтому искомая образующая равна 6.
— равносторонний, поэтому искомая образующая равна 6.
Ответ: ![]()
Задача для самостоятельного решения №7. Образующая конуса равна ![]() и наклонена к плоскости основания под углом
и наклонена к плоскости основания под углом ![]() Найти радиус основания конуса.
Найти радиус основания конуса.
Решение. Длина дуги сектора, образованного разверткой боковой поверхности конуса, равна с одной стороны ![]() а с другой —
а с другой — ![]() — длина окружности основания конуса. Откуда получаем, что
— длина окружности основания конуса. Откуда получаем, что ![]() Но это же отношение есть синус угла между образующей и высотой конуса. Итак, искомый угол есть
Но это же отношение есть синус угла между образующей и высотой конуса. Итак, искомый угол есть ![]()
Ответ: ![]()
Задача для самостоятельного решения №8. Высота конуса равна ![]() а радиус основания равен
а радиус основания равен ![]() Вычислите площадь полной поверхности правильной четырехугольной пирамиды, вписанной в этот конус.
Вычислите площадь полной поверхности правильной четырехугольной пирамиды, вписанной в этот конус.
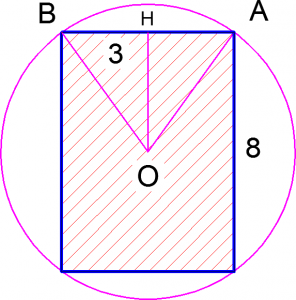
Задачи по стереометрии из ЕГЭ, связанные со сферой
Решение. ![]()
![]() тогда из прямоугольного треугольника
тогда из прямоугольного треугольника ![]() по теореме Пифагора находим
по теореме Пифагора находим ![]()
Ответ: ![]()
Задача для самостоятельного решения №9. Найдите диаметр сферы, описанной около прямоугольного параллелепипеда, ребра которого равны ![]()
![]()
![]()
Итак, подведем итог. Что нужно для успешного решения задач по стереометрии из ЕГЭ?
- знание основных формул для нахождения значений геометрических величин пространственных фигур;
- умение проводить дополнительные построение и доказательства верности этих построений;
- верно выполнять арифметические преобразования численных и буквенных выражений.
До экзамена осталось совсем мало времени и использовать его нужно максимально эффективно. К примеру, тренируйтесь в выполнении заданий, которые вызывают наибольшие затруднения. Помните, от того насколько хорошо вы сдадите выпускные экзамены в какой-то мере зависит ваша дальнейшая жизнь. Успехов вам!
Репетитор по математике на Тёплом Стане
Сергей Валерьевич
© Нильс Г. Абель

В примере №4 «Найдите расстояние от вершины A до грани PCD.»
До самой грани, а не до плоскости содержащей грань. Нужно найти высоту в треугольнике АРD.
Расстояние до плоскости боковой грани.
Пример №10
Возьмём пирамиду в основании которой прямоугольник со сторонами 6 и 8. Рассмотрим диагональные сечения. Они представляют собой равные равнобедренные треугольники. Значит углы наклона рёбер к основанию ( углы при основании диагональных сечений) равны. Отсюда вывод: в основании пирамиды не обязательно квадрат.
Где у меня ошибка?
Согласен, не обязательно квадрат. Всё верно.