Как решать задачи C2 ЕГЭ по математике — советы репетитора

Как научиться решать задачи C2 из ЕГЭ по математике? Этот вопрос в преддверии экзамена возникает у будущих выпускников все чаще. Как репетитор по математике, в течении длительного времени занимающийся подготовкой школьников к сдаче ЕГЭ, раскрою сегодня несколько связанных с этим секретов. Существует три основных метода решения задач C2 из ЕГЭ по математике. Условно назовем их «методом построений», «векторным методом» и «методом объемов». Каждый из них удобен в том или ином случае, поэтому лучше знать и уметь использовать все три (совет репетитора по математике).

Наиболее универсальным является «метод построений», с его помощью можно решить практически любую задачу по стереометрии из тех, что предлагаются в вариантах ЕГЭ по математике. Однако, он не всегда целесообразен с точки зрения временных и вычислительных затрат. В этом случае на помощь приходят два оставшихся метода. Но обо всем по порядку.

Итак, что же нужно, чтобы решать задачи C2 с использованием «метода построений». Необходимым (но, конечно, не достаточным) условием является безупречное знание и понимание основных теорем стереометрии, связанных с взаимным расположением прямых и плоскостей в пространстве. Они потребуются для доказательств, которые непременно сопровождают решение практически любой задачи C2, без которых часть баллов за это задание на экзамене может быть потеряна. Приведем в справочном виде основные из этих теорем.

1. Признак параллельности прямой и плоскости

Признак параллельности прямой и плоскости

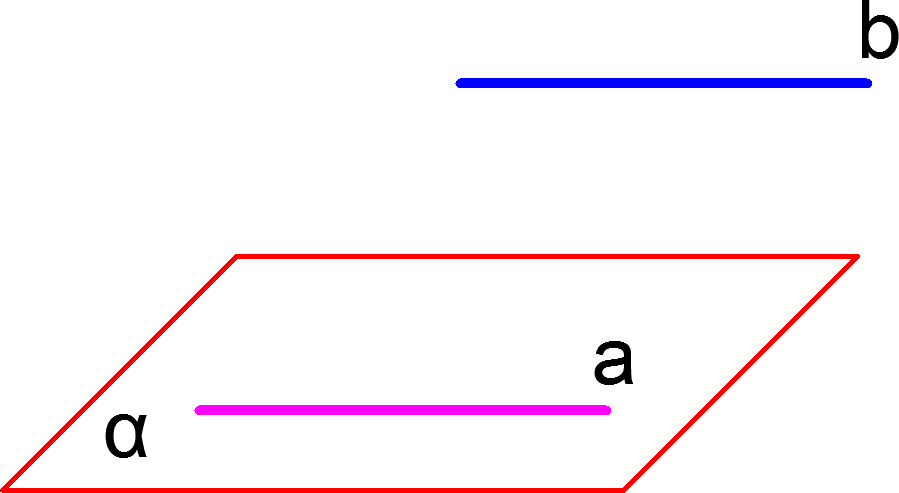
Если прямая не лежит в плоскости и параллельна какой-нибудь прямой, лежащей в данной плоскости, то она параллельна этой плоскости. На рисунке прямая не лежит в плоскости но при этом она параллельна прямой лежащей в плоскости следовательно прямая параллельна плоскости

2. Признак параллельности плоскостей

Признак параллельности плоскостей

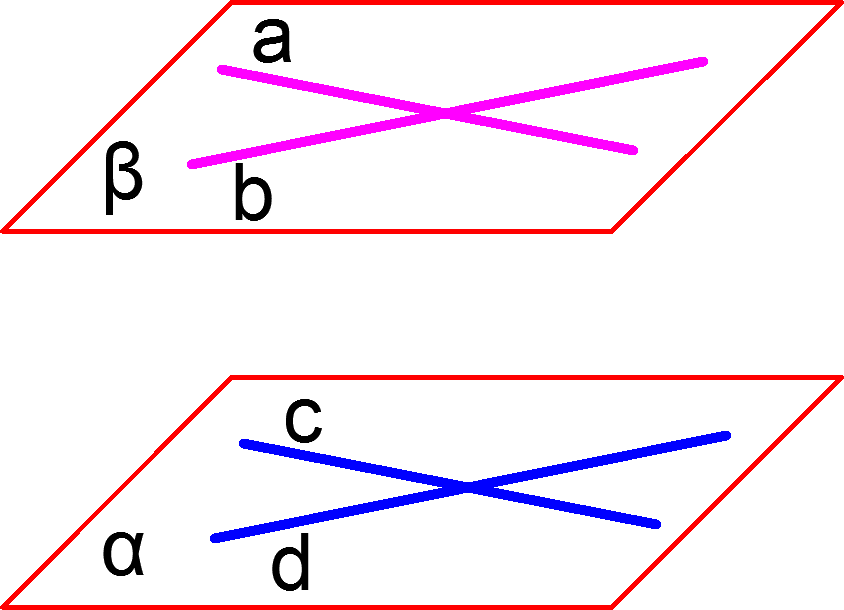
Если две пересекающиеся прямые, принадлежащие одной плоскости, соответственно параллельны двум прямым, принадлежащим другой плоскости, то такие плоскости параллельны. На рисунке прямые и принадлежат плоскости и пересекаются, прямые и принадлежат плоскости и пересекаются, кроме того прямая параллельна прямой , а прямая параллельна прямой поэтому плоскости и параллельны.

3. Признак перпендикулярности прямой и плоскости

Признак перпендикулярности прямой и плоскости

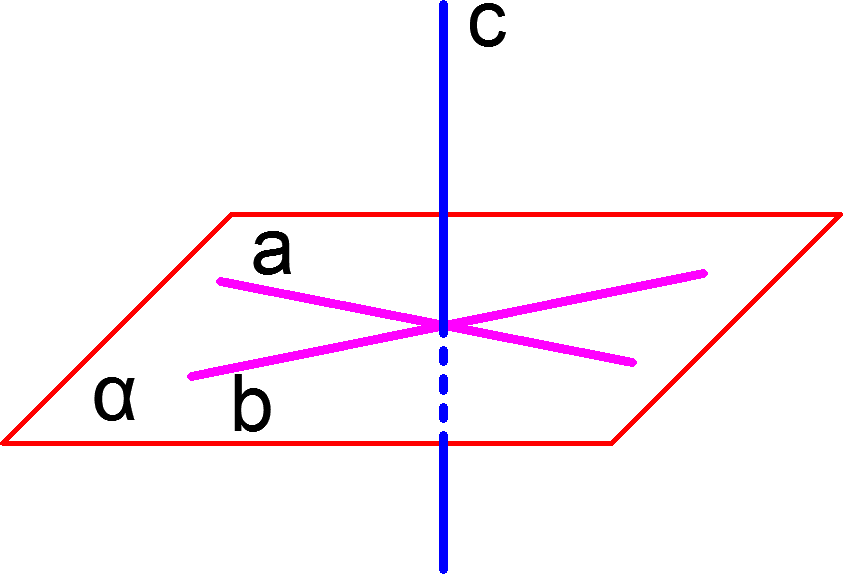
Если прямая перпендикулярна двум пересекающимся прямым, принадлежащим данной плоскости, то такая прямая перпендикулярна этой плоскости. На рисунке прямые и лежат в плоскости и пересекаются, прямая перпендикуляра и прямой и прямой следовательно прямая перпендикулярна плоскости

4. Теорема о трех перпендикулярах

Теорема о трех перпендикулярах

Прямая. Прямая, лежащая в плоскости и перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и к самой наклонной.

Обратная. Прямая, лежащая в плоскости и перпендикулярная наклонной, перпендикулярна и проекции этой наклонной на данную плоскость.

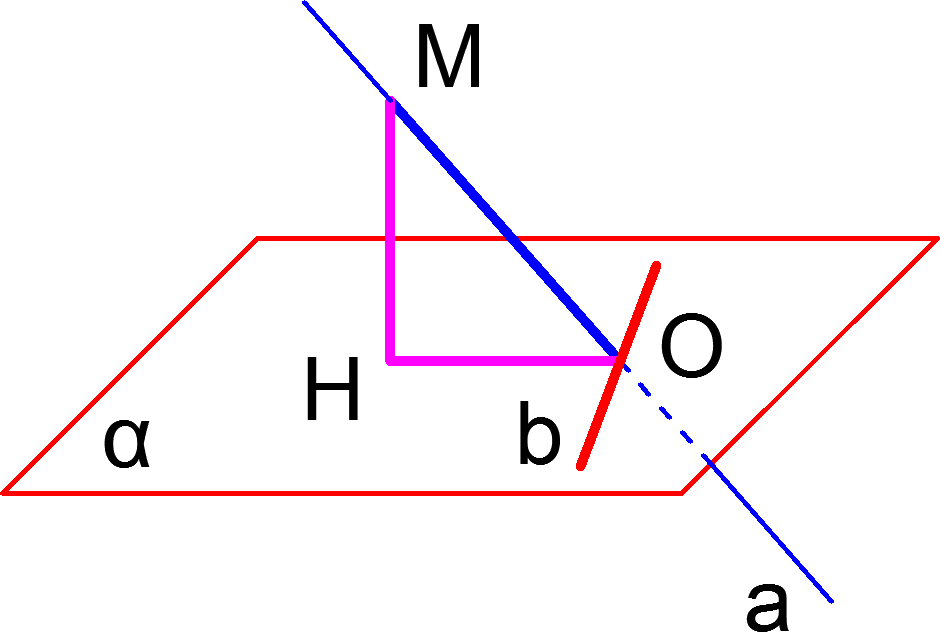
На рисунке наклонная пересекает плоскость в точке Из точки принадлежащей прямой опущен перпендикуляр к плоскости основанием этого перпендикуляра служит точка отрезок — проекция наклонной на плоскость В плоскости проведена прямая перпендикулярно проекции значит прямая перпендикулярна и самой наклонной Верно и обратное.

5. Признак перпендикулярности плоскостей

Признак перпендикулярности плоскостей

Если плоскость проходит через прямую, которая перпендикулярна другой плоскости, то такие плоскости перпендикулярны. На рисунке прямая перпендикулярна плоскости плоскость проходит через прямую поэтому плоскость перпендикулярна плоскости

Кроме знания этих теорем вам потребуется умение строить искомые в задачах углы и расстояния. В виде справки напомним, что понимается под расстояниями и углами между прямыми и плоскостями в стереометрии.

Разберем несколько примеров.

Пример 1. В правильной четырехугольной пирамиде все ребра которой равны найдите косинус угла между прямой и плоскостью

Рисунок к задаче

Решение. В пирамиде проведем высоту тогда точка — центр основания Соединим ее с серединой ребра — средняя линия треугольника значит и поэтому угол между и плоскостью равен углу между и этой плоскостью.

В треугольнике проведем мысленно высоту Докажем, что Несложно доказать, что (сделайте это самостоятельно). Из этого следует, что перпендикулярна любой прямой, лежащей в плоскости в том числе и Кроме того перпендикулярна по построению. Получается, что перпендикулярна двум пересекающимся прямым плоскости а потому перпендикулярна этой плоскости.

тогда можно рассматривать как наклонную к плоскости а — как ее проекцию на эту плоскость. Значит — по определению угол между прямой и плоскостью находим из теоремы Пифагора для прямоугольного треугольника Получаем, что Из прямоугольного треугольника по определению находим

Пример 2. В правильной шестиугольной призме стороны основания которой равны а боковые ребра равны найдите расстояние от точки до прямой

Чертеж к решению

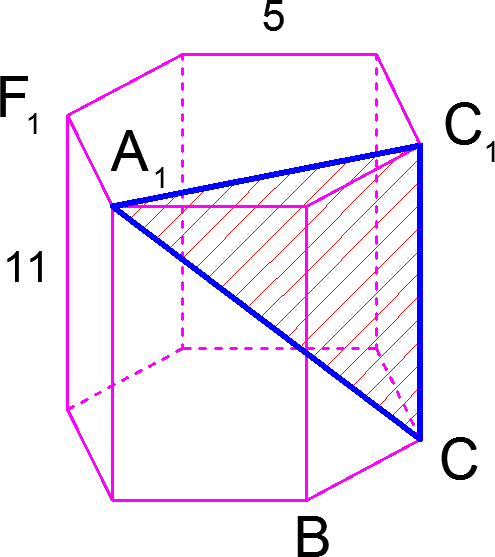
Решение. Посмотрите на изображенный рисунок к задаче. В основаниях правильной шестиугольной призмы лежат правильные шестиугольники, все углы которых равны, как известно, по Докажите самостоятельно, что Сей факт непосредственно следует из свойств правильного шестиугольника, которые вы изучали на уроках геометрии в девятом классе.

так как призма правильная, поэтому можно рассмотреть как наклонную к плоскости , а — как проекцию этой наклонной на данную плоскость. Прямая лежит в плоскости и перпендикулярна проекции а значит по теореме, обратной теореме о трех перпендикулярах, перпендикуляра и самой наклонной То есть — искомое расстояние.

Из теоремы косинусов для треугольника находим  (проведите расчет самостоятельно). Тогда из теоремы Пифагора для прямоугольного треугольника получаем, что то есть

«Метод построений», как было сказано, универсален и подходит для решения практически любой задач C2 по математике, но при этом зачастую приходится проводить множество различных доказательств, поэтому его не всегда можно назвать целесообразным. В том случае, если требуется найди угол между двумя прямыми, иногда удобнее использовать так называемый «векторный метод». Разберемся в чем его суть.

Под скалярным произведением векторов понимают:  где — угол между векторами.

Если координаты вектора а координаты вектора то скалярное произведение находится по формуле:

Если известны координаты вектора то его длина находится по формуле:

Пример 3. В правильной треугольной призме все ребра которой равны найдите косинус угла между прямыми и

Решение.

1. «Метод построений»

«Метод построений»

Прямая принадлежит плоскости прямая пересекает эту плоскость в точке не лежащей на прямой следовательно, прямые и являются скрещивающимися по соответствующему признаку. Через точку проведем прямую, параллельную прямой пусть — точка пересечения этой прямой и плоскости тогда — искомый по определению угла между скрещивающимися прямыми.

Ищем стороны треугольника — параллелограмм по построению, его противоположные стороны равны по соответствующему признаку, то есть В основаниях правильной треугольной призмы лежат правильные треугольники, каждый из углов которых, как известно, равен по Значит как смежный с углом в Сторону находим по теореме косинусов для треугольника получаем (выполните расчет самостоятельно). Сторону находим по теореме Пифагора для прямоугольного треугольника получаем то есть Сторону находим по теореме Пифагора для прямоугольного треугольника получаем то есть

Зная три стороны треугольника, можно найти все его элементы. Искомый угол находим по теореме косинусов для треугольника получаем то есть откуда

2. «Векторный метод»

«Векторный метод»

Обозначим косинус искомого угла Введем прямоугольную декартову систему координат так, как показано на рисунке. Ищем угол между векторами и . Координаты интересующих нас точек (определите их самостоятельно):

Чтобы определить координаты вектора, необходимо из координат точки, являющейся его концом, соответствующим образом вычесть координаты точки, являющейся его началом. То есть:

Искать длины данных векторов, используя соотношение  в данном случае нецелесообразно. Гораздо проще найти их из геометрии рисунка: Скалярное произведение равно, как известно, сумме произведений соответствующих координат, то есть в нашем случае С другой стороны:   Приравниванием правых частей последних двух выражений получаем

Второй случай, когда не всегда целесообразно использовать «метод построений», связан с нахождением расстояния от точки до плоскости. Здесь на помощь может прийти так называемый «метод объемов». Из теории здесь вам понадобится лишь знание формулы объема произвольной пирамиды (кто не помнит, здесь — площадь основания пирамиды, — ее высота).

Пример 4. В единичном кубе найдите расстояние от точки до плоскости

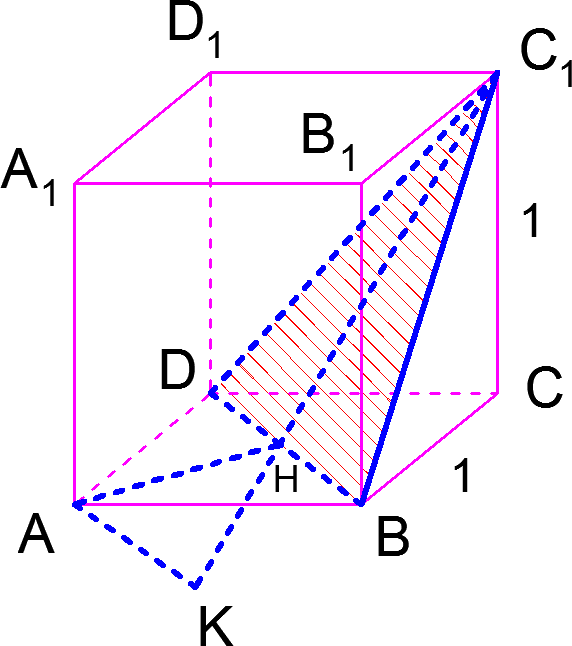
Решение.

1. «Метод построений»

«Метод построений»

В треугольнике проведем высоту соединим точки и . Искомое расстояние — высота треугольника Докажем это. по построению. — наклонная к плоскости — проекция этой наклонной на данную плоскость, лежит в этой плоскости и перпендикулярна проекции по построению, значит перпендикулярна и самой наклонной по теореме, обратной теореме о трех перпендикулярах, то есть . Получается, что перпендикулярна двум пересекающимся прямым плоскости а значит по признаку перпендикулярности прямой и плоскости перпендикулярна этой плоскости.

Найдем стороны треугольника (половина диагонали квадрата), — диагональ куба, находим из прямоугольного треугольника по теореме Пифагора: Из теоремы косинусов для треугольника получаем, что то есть тогда Ищем площадь треугольника она равна С другой стороны это Приравнивая, получаем

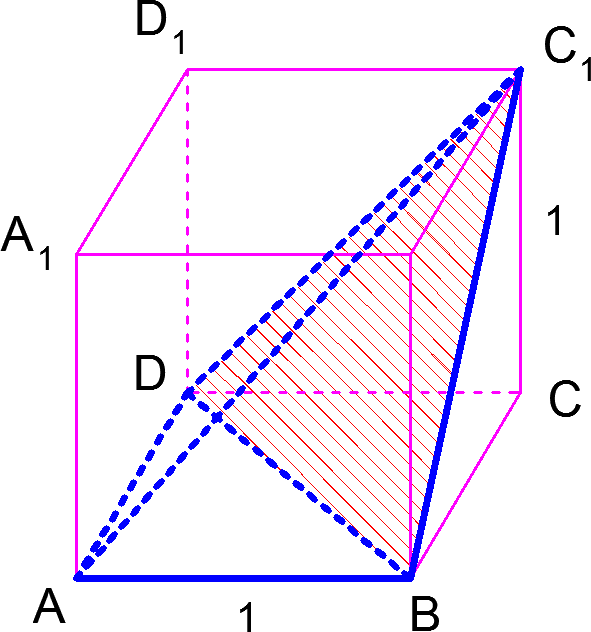
2. «Метод объемов»

«Метод объемов»

Рассмотрим пирамиду Вычислим ее объем двумя способами. Возьмем сперва в качестве основания грань площадь которой равна (докажите самостоятельно), высота пирамиды в этом случае Тогда ее объем равен Теперь в качестве основания возьмем грань площадь которой равна (проведите расчет самостоятельно). Тогда объем равен Приравнивая получаем,

На этом на сегодня все. Задавайте свои вопросы в комментариях, подписывайтесь на обновления. А напоследок очередное ближневосточное мудрое изречение, как нельзя лучше подходящее к тяжкой проблеме поиска по-настоящему нужных и ценных знаний.

Ваш профессиональный
репетитор по физике и математике
Сергей Валерьевич