В этой статье я расскажу об одном эффективном способе решения иррациональных неравенств. То есть таких неравенств, которые содержат неизвестную величину под знаком корня. Данный материал очень редко изучается в школа. Разве что в школе с углублённым изучением математики, да и то не всегда. А ведь научиться решать иррациональные неравенства, используя этот способ, очень важно. Поэтому дочитайте эту статью до конца или посмотрите мой видеоурок (ссылка ниже в тексте). Информация, которую вы получите, может очень пригодиться при сдаче ОГЭ, ЕГЭ или вступительных экзаменов по математике.
Иррациональные неравенства, как и любые другие, изучаемые в школьном курсе математики, можно решить с помощью метода интервалов. Но есть более простой и эффективный способ. Разберёмся, в чём он заключается. Все наиболее часто встречающиеся иррациональные неравенства из школьного курса математики можно условно разделить на два типа:
1. ![]() или
или ![]() .
.
2. ![]() или
или ![]() .
.
Здесь ![]() и
и ![]() — некоторые выражения относительно переменной
— некоторые выражения относительно переменной ![]() . Разберём отдельно решение каждого из этих двух типов иррациональных неравенств.
. Разберём отдельно решение каждого из этих двух типов иррациональных неравенств.
Решение иррациональных неравенств первого типа
Рассмотрим внимательно неравенство ![]() . Как уже отмечалось,
. Как уже отмечалось, ![]() и
и ![]() — это некоторые выражения относительно переменной
— это некоторые выражения относительно переменной ![]() . Но при определённых значениях
. Но при определённых значениях ![]() эти выражения будут принимать какие-то определённые значения. Наша задача состоит в том, чтобы найти такие значения переменной
эти выражения будут принимать какие-то определённые значения. Наша задача состоит в том, чтобы найти такие значения переменной ![]() , при которых значение выражения
, при которых значение выражения ![]() будет больше значения выражения
будет больше значения выражения ![]() . Извините, что я говорю очевидные вещи. В данной статье я решил объяснить всё предельно подробно. Если эти разъяснения кажутся вам излишними, вы можете пропустить их и перейти непосредственно к примерам в красных рамочках.
. Извините, что я говорю очевидные вещи. В данной статье я решил объяснить всё предельно подробно. Если эти разъяснения кажутся вам излишними, вы можете пропустить их и перейти непосредственно к примерам в красных рамочках.
Чтобы избавиться от корня, нужно возвести обе части неравенства в квадрат. Тогда неравенство примет вид: ![]() . Но просто так, без соблюдения определённых правил, этого делать нельзя. Почему? Представьте, что при каком-то значении
. Но просто так, без соблюдения определённых правил, этого делать нельзя. Почему? Представьте, что при каком-то значении ![]() значение выражения
значение выражения ![]() равно, скажем,
равно, скажем, ![]() , а значение выражения
, а значение выражения ![]() равно, например,
равно, например, ![]() . Такое возможно? Вполне. Тогда, подставив эти значения в неравенство
. Такое возможно? Вполне. Тогда, подставив эти значения в неравенство ![]() , получившееся после возведения обеих частей в квадрат, мы получим верное неравенство
, получившееся после возведения обеих частей в квадрат, мы получим верное неравенство ![]() . Всё будет хорошо, и мы воспримем то значение
. Всё будет хорошо, и мы воспримем то значение ![]() , которое взяли, как решение нашего иррационального неравенства.
, которое взяли, как решение нашего иррационального неравенства.
Но проблема в том, что если значение ![]() подставить вместо
подставить вместо ![]() в исходное неравенство, то всё уже не будет так прекрасно. Потому что любой школьник знает, что под корнем не может находиться отрицательных чисел! Как видите, возведение обеих частей неравенства в квадрат — операция вовсе не равносильная. Она может привести к появлению лишних решений. Поэтому делая это, нужно обязательно убедиться, что под знаком корня не находится отрицательного числа. То есть, что
в исходное неравенство, то всё уже не будет так прекрасно. Потому что любой школьник знает, что под корнем не может находиться отрицательных чисел! Как видите, возведение обеих частей неравенства в квадрат — операция вовсе не равносильная. Она может привести к появлению лишних решений. Поэтому делая это, нужно обязательно убедиться, что под знаком корня не находится отрицательного числа. То есть, что ![]() .
.
Теперь представим ситуацию, что при каком-то значении ![]() значение выражения
значение выражения ![]() равно
равно ![]() , а значение выражения
, а значение выражения ![]() равно, например,
равно, например, ![]() . Верно ли наше исходное неравенство? Конечно, нет. Всем понятно, что корень из
. Верно ли наше исходное неравенство? Конечно, нет. Всем понятно, что корень из ![]() , то есть
, то есть ![]() , не меньше
, не меньше ![]() . Но что будет если мы вновь возведём обе части нашего неравенства в квадрат? Получим неравенство
. Но что будет если мы вновь возведём обе части нашего неравенства в квадрат? Получим неравенство ![]() . А вот это уже верно. И снова мы получили лишнее решение, которое не удовлетворяет исходном неравенству. Чтобы этого не случилось, нужно сказать дополнительно, что
. А вот это уже верно. И снова мы получили лишнее решение, которое не удовлетворяет исходном неравенству. Чтобы этого не случилось, нужно сказать дополнительно, что ![]() .
.
Есть ли ещё какие-нибудь неприятные моменты, которые мы не учли при возведении обеих частей неравенства в квадрат? Разве что один. Что делать, если найдётся такое значение ![]() , при котором и значение выражения
, при котором и значение выражения ![]() , и значение выражения
, и значение выражения ![]() равны нулю? Что ж, если неравенство строгое, как в нашем случае, когда
равны нулю? Что ж, если неравенство строгое, как в нашем случае, когда ![]() , то этот случай ничего не меняет, ведь нуль не меньше нуля. А вот если исходное неравенство нестрогое, то есть
, то этот случай ничего не меняет, ведь нуль не меньше нуля. А вот если исходное неравенство нестрогое, то есть ![]() , тогда это уже имеет значение, ведь нуль меньше или равен нулю! В этом случае все условия также должны быть нестрогими, поэтому
, тогда это уже имеет значение, ведь нуль меньше или равен нулю! В этом случае все условия также должны быть нестрогими, поэтому ![]() .
.
Итак, исходя из всех этих долгих пояснений, мы делаем вывод, что иррациональное неравенство вида ![]() равносильно следующей системе неравенств:
равносильно следующей системе неравенств:
![Rendered by QuickLaTeX.com \[ \begin{cases} f(x)<g^2(x) \\ f(x)\geqslant 0 \\ g(x)>0. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-1d6f90693d0edb446f64939cafef603a_l3.png)
А иррациональное неравенство вида ![]() , в свою очередь, равносильно следующей системе неравенств:
, в свою очередь, равносильно следующей системе неравенств:
![Rendered by QuickLaTeX.com \[ \begin{cases} f(x)\leqslant g^2(x) \\ f(x)\geqslant 0 \\ g(x)\geqslant 0. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e88f4662f26fe8332ba1362d8611c323_l3.png)
| Пример 1. Требуется решить неравенство:
|
Для решения иррационального неравенства переходим к равносильной системе неравенств:
![Rendered by QuickLaTeX.com \[ \begin{cases} x-2 <\left(\frac{x}{3}\right)^2 \\ x-2\geqslant 0 \\ \frac{x}{3}>0 \end{cases}\Leftrightarrow \begin{cases} x^2-9x+18>0 \\ x\geqslant 2 \\ x>0. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-38a172c9bf7f851273a82910b42c966d_l3.png)
Условие ![]() «сильнее» условия
«сильнее» условия ![]() , поэтому последнее неравенство системы можно отбросить. Решаем квадратичное неравенство. Для этого находим корни уравнения
, поэтому последнее неравенство системы можно отбросить. Решаем квадратичное неравенство. Для этого находим корни уравнения ![]() , они равны
, они равны ![]() и
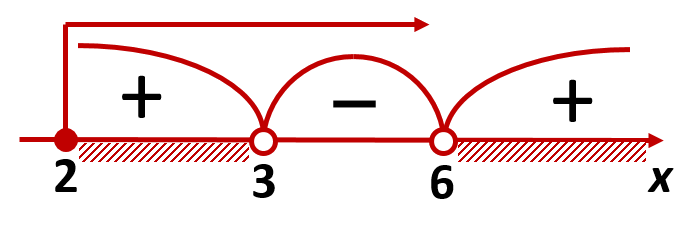
и ![]() . Теперь строим кривую знаков и стрелкой отмечаем на ней условие
. Теперь строим кривую знаков и стрелкой отмечаем на ней условие ![]() :
:
Получаем следующий ответ к неравенству: ![]() .
.
Решение иррациональных неравенств второго типа
Рассмотрим теперь иррациональное неравенство вида ![]() . Как и в предыдущем случае, безусловным требованием является отсутствие под знаком корня отрицательных чисел. То есть должно выполняться условие
. Как и в предыдущем случае, безусловным требованием является отсутствие под знаком корня отрицательных чисел. То есть должно выполняться условие ![]() . При этом выражение
. При этом выражение ![]() тоже, конечно, является неотрицательным. Пусть, например, при некотором значении
тоже, конечно, является неотрицательным. Пусть, например, при некотором значении ![]() оно равно
оно равно ![]() . Если при этом же значении
. Если при этом же значении ![]() , значение выражения
, значение выражения ![]() отрицательно, то есть
отрицательно, то есть ![]() (например, это значение равно
(например, это значение равно ![]() ), то мы получаем верное неравенство
), то мы получаем верное неравенство ![]() . И никаких дополнительных требований уже не нужно.
. И никаких дополнительных требований уже не нужно.
Что если выражение ![]() принимает неотрицательные значения, то есть
принимает неотрицательные значения, то есть ![]() ? Например, пусть при каком-то значении
? Например, пусть при каком-то значении ![]() значение выражения
значение выражения ![]() равно
равно ![]() , а значение выражения
, а значение выражения ![]() равно
равно ![]() . Тогда верно как исходное неравенство
. Тогда верно как исходное неравенство ![]() , так и неравенство, полученное после возведения обеих частей в квадрат
, так и неравенство, полученное после возведения обеих частей в квадрат ![]() . Как видите, в этом случае мы уже можем возводить обе части неравенства в квадрат, не боясь получить посторонние решения. При этом, раз уж мы требуем, чтобы
. Как видите, в этом случае мы уже можем возводить обе части неравенства в квадрат, не боясь получить посторонние решения. При этом, раз уж мы требуем, чтобы ![]() , то из условия
, то из условия ![]() автоматически следует условие
автоматически следует условие ![]() , о выполнении которого, получается, можно не беспокоиться.
, о выполнении которого, получается, можно не беспокоиться.
Какие ещё подводные камни могут возникнуть при решении иррационального неравенства второго типа? Как и для иррационального неравенства первого типа, стоит отдельно рассмотреть случай, когда при каком-то значении переменной ![]() и значение выражения
и значение выражения ![]() , и значение выражения
, и значение выражения ![]() равны нулю. Этот случай имеет значение только если неравенство нестрогое. Тогда неравенство, полученное после возведения обеих частей исходного иррационального неравенства в квадрат, тоже должно быть нестрогим. В случае строгого неравенства ничего не изменится.
равны нулю. Этот случай имеет значение только если неравенство нестрогое. Тогда неравенство, полученное после возведения обеих частей исходного иррационального неравенства в квадрат, тоже должно быть нестрогим. В случае строгого неравенства ничего не изменится.
Итак, исходя из всего вышеизложенного, можно заключить, что неравенство вида ![]() равносильно следующей совокупности из двух систем неравенств:
равносильно следующей совокупности из двух систем неравенств:
![Rendered by QuickLaTeX.com \[ \left[ \begin{array}{l} \begin{cases} g(x)\geqslant 0\\ f(x)>g^2(x) \end{cases} \\ \begin{cases} f(x)\geqslant 0 \\ g(x)<0. \end{cases} \end{array} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-b7381284173508904e0ed4ac088073fa_l3.png)
Ну а неравенство вида ![]() равносильно следующей совокупности из двух систем неравенств:
равносильно следующей совокупности из двух систем неравенств:
![Rendered by QuickLaTeX.com \[ \left[ \begin{array}{l} \begin{cases} g(x)\geqslant 0\\ f(x)\geqslant g^2(x) \end{cases} \\ \begin{cases} f(x)\geqslant 0 \\ g(x)< 0. \end{cases} \end{array} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4b989fd31a1f1d81eabf9821f4b52769_l3.png)
Квадратная скобка обозначает совокупность, то есть объединение решений каждой из систем неравенств.
| Пример 2. Требуется решить неравенство:
|
Для решения данного иррационального неравенства перейдём к следующей равносильной совокупности:
![Rendered by QuickLaTeX.com \[ \left[ \begin{array}{l} \begin{cases} \frac{x-1}{2}\geqslant 0\\ x-2\geqslant \left(\frac{x-1}{2}\right)^2 \end{cases} \\ \begin{cases} x-2\geqslant 0 \\ \frac{x-1}{2}< 0. \end{cases} \end{array}\Leftrightarrow \left[ \begin{array}{l} \begin{cases} x\geqslant 1 \\ x^2-6x+9\leqslant 0 \end{cases} \\ \begin{cases} x\geqslant 2 \\ x< 1. \end{cases} \end{array} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-774a887b429f29a3b63e4a9a7a3a3b32_l3.png)
В первой системе неравенство ![]() можно преобразовать по формуле «квадрат разности» к виду
можно преобразовать по формуле «квадрат разности» к виду ![]() , которое выполняется при одном единственном значении
, которое выполняется при одном единственном значении ![]() (при всех остальных значениях x выражение
(при всех остальных значениях x выражение ![]() положительно, потому что это полный квадрат). Это условие удовлетворяет требованию
положительно, потому что это полный квадрат). Это условие удовлетворяет требованию ![]() . Что касается второй системы, то для неё нет ни одного значения
. Что касается второй системы, то для неё нет ни одного значения ![]() , при которых были бы выполнены оба условия одновременно. То есть решений данная система не имеет. Тогда в итоге в ответе получаем одно единственное число:
, при которых были бы выполнены оба условия одновременно. То есть решений данная система не имеет. Тогда в итоге в ответе получаем одно единственное число: ![]() .
.
Ну и напоследок решим более сложное иррациональное неравенство, чтобы показать, что даже более сложные случаи сводятся к тем двум типам иррациональных неравенств, решение которых описано в данной статье.
| Пример 3. Решите неравенство:
|
Перенесём второй радикал (корень) в правую часть неравенства с противоположным знаком. В результате данного преобразования получим такое неравенство:
![]()
Это уже неравенство вида ![]() , поэтому можно перейти к следующей равносильной системе:
, поэтому можно перейти к следующей равносильной системе:
![Rendered by QuickLaTeX.com \[ \begin{cases} x^2+3x+2\geqslant 0 \\ x^2-x+1\geqslant 0 \\ x^2+3x+2<\left(1+\sqrt{x^2-x+1}\right)^2. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-27a0a4c1dc974e1351ce2f7fa04d6bc5_l3.png)
Обращаем сразу внимание, что второе неравенство системы выполняется при любых значениях ![]() . Действительно, ветви соответствующей параболы направлены вверх, а дискриминант соответствующего квадратичного уравнения отрицателен, то есть эта парабола нигде не пересекает ось абсцисс. Поэтому соответствующая квадратичная функция принимает только положительные значения. Первое неравенство решается методом интервалов. Теперь в последнем неравенстве нужно раскрыть скобки и упростить полученное выражение. В результате получаем следующую систему:
. Действительно, ветви соответствующей параболы направлены вверх, а дискриминант соответствующего квадратичного уравнения отрицателен, то есть эта парабола нигде не пересекает ось абсцисс. Поэтому соответствующая квадратичная функция принимает только положительные значения. Первое неравенство решается методом интервалов. Теперь в последнем неравенстве нужно раскрыть скобки и упростить полученное выражение. В результате получаем следующую систему:
![Rendered by QuickLaTeX.com \[ \begin{cases} x\leqslant -2,\, x\geqslant -1 \\ \sqrt{x^2-x+1}>2x. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c761bd8e11c34334e95731acc44d6f20_l3.png)
Последнее неравенство системы — это иррациональное неравенство вида ![]() . Его можно представить в виде равносильной ему совокупности, о которой я подробно рассказывал выше. В результате получаем следующую равносильную систему:
. Его можно представить в виде равносильной ему совокупности, о которой я подробно рассказывал выше. В результате получаем следующую равносильную систему:
![Rendered by QuickLaTeX.com \[ \left[ \begin{array}{l} \begin{cases} x\leqslant -2,\, -1\leqslant x< 0 \\ x^2-x+1\geqslant 0 \end{cases} \\ \begin{cases} x\geqslant 0 \\ 3x^2+x-1<0. \end{cases} \end{array} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f17c1778c0626150e97c05a2dff809c0_l3.png)
Дальше всё решается стандартными способами, которые уже были рассмотрены в данной статье. Попробуйте дорешать этот пример до конца самостоятельно. Внимание спойлер! Окончательный ответ к неравенству будет выглядеть следующим образом:
![Rendered by QuickLaTeX.com \[ x\in(-\mathcal{1};-2]\cup\left[-1;\frac{\sqrt{13}-1}{6}\right). \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-41a5d414d739620de99e15f309dce460_l3.png)
Вот такой способ решения иррациональных неравенств. Запомните его, он вам пригодится на экзамене по математике, будь то ОГЭ, ЕГЭ или дополнительное вступительное испытание при поступлении в ВУЗ.
Проверьте, насколько хорошо вы усвоили материал урока. Выполните следующие задания самостоятельно:
- Решите неравенство:
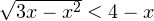 .
.
- Решите неравенство:
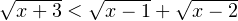 .
.
![Rendered by QuickLaTeX.com \[ x\in\left(\frac{2\sqrt{21}}{3};+\mathcal{1}\right) \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-372a31f4b542496247bcf0718aaf3c1c_l3.png)
Материал подготовлен репетитором по математике, Сергеем Валерьевичем
Смотрите также:

Помогите, пожалуйста, решить второе неравенство, никак не могу получить верный ответ!
Найдите, при каком значении левая часть неравенства равна правой, и докажите, что при всех x, которые больше этого числа, неравенство выполняется.
Здравствуйте, Сергей. А как доказать что при всех значениях x, которые больше этого числа, неравенства выполняется.
Здравствуйте. Область допустимых значений неравенства: x>=2. Обе части неравенства неотрицательны, то есть можно возвести их в квадрат, не меняя при этом знак неравенства. Получаем неравенство 6-x<2*корень((x-1)(x-2)). Решаем теперь уравнение 6-x=2*корень((x-1)(x-2)) возведением обеих частей в квадрат. Получаем один корень, удовлетворяющий условию x>=2. Это корень x = 2*корень(21)/3. Значит график убывающей функции y=6-x пересекает график возрастающей при x>=2 функции y=2*корень((x-1)(x-2)) в точке x = 2*корень(21)/3. Стало быть до пересечения при x>=2 первая функция y=6-x принимала бОльшие значения, чем вторая, а после пересечения станет принимать мЕньшие. Нас интересуют мЕньшие. То есть ответ (2*корень(21)/3;+бесконечность).
Здравствуйте Сергей, помогите пожалуйста решить одно неравенство:
√x^2-x(все в корне)>2√3
Тема понятная, но как у меня,так и у всех одна проблема, поменяли пару чисел или знаков и все, задача невыполнима.
(хотя бы объясните как подобные решаются или вы наверное скажите что я не внимательный, и попросите прочитать еще раз)