
Лицей НИУ ВШЭ официально объявил о проведении дополнительного набора учащихся. Вступительные испытания состоятся в декабре 2019 года. Если вы поступаете на направление «Математика», то помимо комплексного теста вас ожидает ещё и устное собеседование. Примеры заданий собеседования выложены на сайте лицея. В данной статье профессиональный репетитор по математике и физике разбирает примерные задачи устного собеседования для дополнительного набора в лицей ВШЭ 2019 года на направление «Математика».
|
Задание 1. На окружности имеются синие и красные точки. Разрешается добавить или убрать красную точку и поменять цвета ее соседей. Менее двух точек оставлять не разрешается. Пусть первоначально были две точки: одна красная и одна синяя точки. Можно ли через 100 операций получить ровно 50 красных точек? |
Количество красных точек меняется после каждой операции на 1 или на 3, поэтому чётность количества красных точек меняется после каждой операции. Значит, после 100 операций чётность количества красных точек будет той же, что и в самом начале, то есть нечётной (первоначально была 1 красная точка). Значит, ровно 50 красных точек после 100 операций получиться не может.
Ответ: нет.
|
Задание 2. Костя написал два числа, не содержащих в записи нулей, и заменил цифры буквами (разные цифры — разными буквами). Оказалось, что число КРОКОДИЛЛЛ делится на 312 Докажите, что число ГОРИЛЛА не делится на 392. |
Если число делится на 312, то оно делится и на 8. Число делится на 8, если три последние цифры этого числа нули или образуют число, которое делится на 8. У числа КРОКОДИЛЛЛ три последние цифры одинаковые, но не 000. Значит, для ЛЛЛ остаётся единственный вариант быть числом 888, чтобы делиться на 8. Значит, Л = 8. Число ГОРИЛЛА тоже должно делиться на 8, если мы доказываем, что оно делится на 392. Значит число ЛЛА = 88A должно делиться на 8. Это возможно только при A = 0. Но по условию так быть не может. Значит, число ГОРИЛЛА на 392 не делится. Что и требовалось доказать.
|
Задание 3. Дан выпуклый четырехугольник ABCD, в котором AD+BC = CD. Биссектрисы углов ∠BCD и ∠CDA пересекаются в точке S. Докажите, что AS = BS. |
Изобразим ситуацию на рисунке вместе с некоторыми дополнительными построениями:
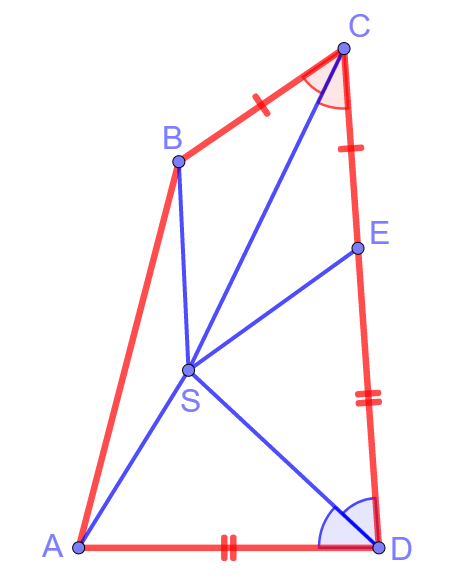
На стороне CD отметили точку E так, что BC = CE. Тогда AD = DE, так как BC + AD = CD. Тогда треугольник ASD равен треугольнику SED по двум сторонами и углу между ними. То есть AS = SE. Аналогично, треугольник SBC равен треугольнику SCE, поэтому SE = SB. Итак, AS = SE = SB. Что и требовалось доказать.
|
Задание 4. Будем называть n-цепочкой число, которое можно получить из чисел от 1 до n, написав их друг за другом в некотором порядке без пробелов. Например, возможный вариант 11-цепочки: 3764581121910. Для какого наименьшего n > 1 существует n-цепочка, являющаяся палиндромом? Напомним, что палиндром — это число, читающееся одинаково слева направо и справа налево, например, 12321 Палиндром не может начинаться с нуля. |
В палиндроме все цифры должны быть разбиты на пары из одинаковых цифр, кроме, может быть, единственного числа, которое стоит в центре, если общее количество цифр в палиндроме нечётно. Определим, для какого минимального n > 1 такое в принципе возможно.
Первый раз такое встречается для n = 19. Тогда получается 12 единиц, 1 нуль, все остальные цифры по 2 раза. Можно привести пример: 91871651431211011213415617819. Итак, минимальное n = 19.
Подробности решения смотрите в прилагаемом видео.
Ответ: 19.
|
Задание 5. В каждой клетке таблицы 4×4 записано натуральное число. Может ли так оказаться, что все 8 сумм по строкам и по столбцам будут различными степенями двойки? |
Докажем сперва вспомогательное неравенство:
![]()
Справа от знака неравенства стоит сумма ![]() членов (так как счёт начинается с нуля) геометрической прогрессии с первым членом
членов (так как счёт начинается с нуля) геометрической прогрессии с первым членом ![]() и знаменателем
и знаменателем ![]() . Эта сумма равна:
. Эта сумма равна:
![]()
Неравенство доказано. Словами его можно сформулировать так: любая натуральная степень двойки со второй и выше строго больше суммы всех предыдущих целых неотрицательных степеней двойки.
Теперь вернёмся к задаче. Пусть удалось расставить числа в таблице требуемым образом. Но тогда среди сумм чисел в каждой строке и столбце найдётся старшая степень двойки. По доказанном выше неравенству, она будет больше всех остальных сумм по строкам и столбцам вместе взятым. Но сумма всех чисел в таблице, вычисленная по строкам, должна быть равна сумме всех чисел в таблице, вычисленной по столбцам, поскольку это одна и та же сумма. Противоречие.
Для знатоков: если это было бы возможно, то сумму всех чисел в таблице, вычисленную по столбцам, можно было бы представить в виде некоторого двоичного числа, а сумму всех чисел в таблице, вычисленную по строкам, можно было бы представить в виде другого двоичного числа. Но это должна быть одна и та же сумма, поэтому и полученные двоичные числа должны быть одинаковы. Противоречие.
Ответ: не может.
|
Задание 6. Каждую грань кубика разбили на четыре одинаковых квадрата, а затем раскрасили эти квадраты в несколько цветов так, что квадраты, имеющие общую сторону, оказались окрашенными в различные цвета. Какое наибольшее количество квадратов одного цвета могло получиться? |
В каждой вершине куба сходится 3 квадрата разного цвета, поскольку каждая пара таких квадратов имеют общую сторону. Всего таких троек 8. Значит оценка даёт максимум 8 квадратов одного цвета. Эти 8 квадратов изображены на рисунке синим цветом, при этом пустые квадраты могут быть закрашены в любые другие различные цвета:
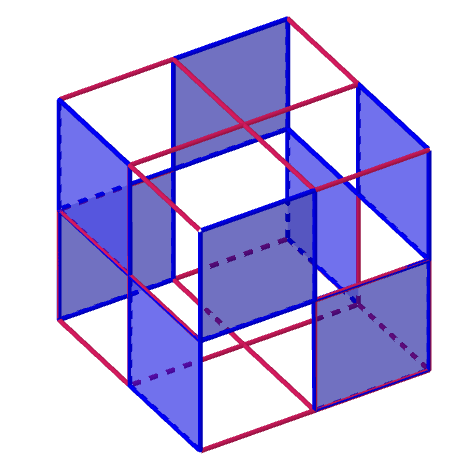
|
Задание 7. Прямоугольник с целыми длинами сторон разбит на двенадцать квадратов со следующими длинами сторон: 2, 2, 3, 3, 5, 5, 7, 7, 8, 8, 9, 9. Каков периметр прямоугольника? |
Площадь исходного прямоугольника равна:
![]()
Так как есть квадраты со стороной 9, то возможен единственный вариант для длин сторон исходного прямоугольника: 16 на 29. Значит, его периметр равен 90. На рисунке представлен пример соответствующего разбиения данного прямоугольника на квадраты:
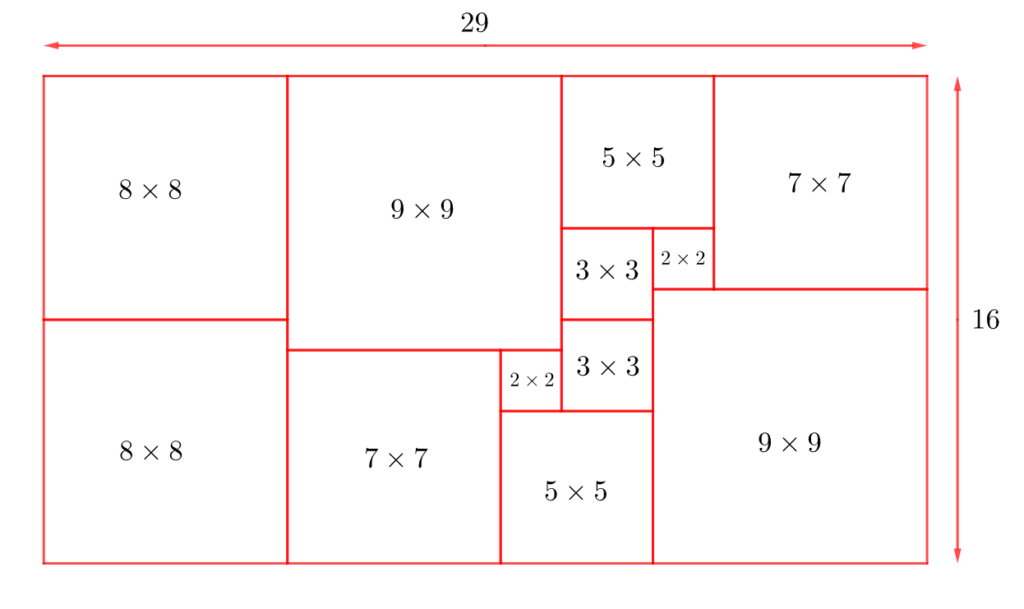
|
Задание 8. Рассмотрим прямоугольник из 2 строк и 2019 столбцов. Нужно закрасить каждую клетку в один из трех цветов так, чтобы соседние по стороне клетки были разных цветов. Сколько существует различных раскрасок? |
Первую клетку первого столбца можно закрасить тремя различными способами. Для каждого способа есть два варианта раскраски второй клетки первого столбца. То есть раскрасить первый столбец можно ![]() различными способами. Далее для каждого варианта раскраски предыдущей части таблицы существует только 3 независимых способа раскраски следующего столбца. Значит, общее число вариантов раскраски равно:
различными способами. Далее для каждого варианта раскраски предыдущей части таблицы существует только 3 независимых способа раскраски следующего столбца. Значит, общее число вариантов раскраски равно:
![]()
Ответ: ![]()
|
Задание 9. В трапеции ABCD точки M и N являются серединами оснований AB и CD соответственно. Точка P принадлежит отрезку MN. Докажите, что площади треугольников ADP и BCP равны. |
Изобразим ситуацию на рисунке:
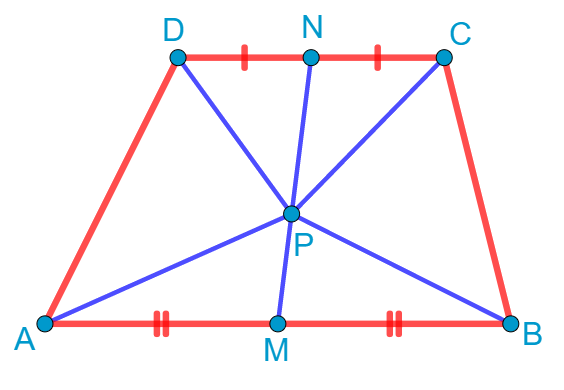
Площади трапеций ADNM и MNCB равны, так как у них равны основания и высоты. Площади треугольников PDN и PCN равны, так как у них равны основания и высоты. По той же причине равны площади треугольников APM и MPB. Значит, оставшиеся части, а именно треугольники ADP и CPB, также равны по площади. Что и требовалось доказать.
|
Задание 10. Точка D лежит на дуге BC описанной окружности равностороннего треугольника ABC, не содержащей точки A. Точка E симметрична B относительно прямой CD. Докажите, что точки A, D и E лежат на одной прямой. |
Изобразим ситуацию на рисунке вместе с некоторыми дополнительными построениями:
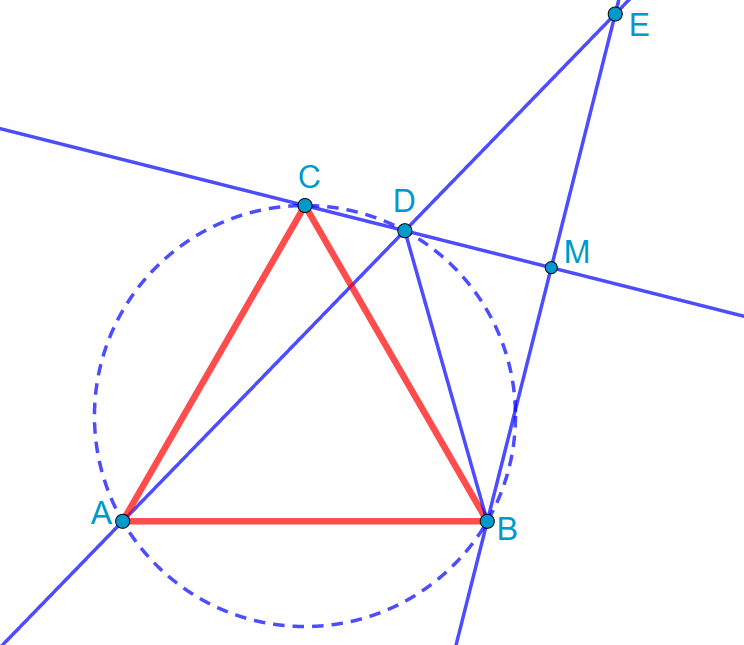
Заметим, что ∠EDM = ∠CDA = ∠CBA = 60° (вертикальные углы и вписанные углы, опирающиеся на одну дугу). По той же причине ∠ADB = ∠ACB = 60°. Кроме того, ∠EDM = ∠MDB = 60°, так как точка E симметрична точке B относительно прямой CD. Значит, ∠ADE = 180°. То есть точки A, D и E лежат на одной прямой. Что и требовалось доказать.
Подготовка к устному собеседованию в лицей ВШЭ на направление «Математика»
Тем, кто готовится к поступлению в лицей НИУ ВШЭ на направление «Математика», может потребоваться помощь профессионального репетитора, особенно при подготовке к самой сложной части вступительных испытаний, а именно к устному собеседованию. Обращайтесь к опытным и проверенным преподавателям. Только они смогут в сжатые сроки максимально эффективно подготовить ученика к вступительным экзамена в лицей ВШЭ. Контакты такого репетитора вы найдёте на этой странице. Успехов в подготовке!
Материал подготовил репетитор по математике и физике в Москве Сергей Валерьевич

Добавить комментарий