Текстовые задачи B13 из ЕГЭ по математике

Текстовая задача B13 из ЕГЭ по математике посвящена решению математических задач или, как их еще называют, задач на составление уравнений. Все эти задачи можно условно разбить на три большие группы: задачи на движение, задачи на работу и задачи на растворы, расплавы, проценты и доли. Как репетитор по математике, занимающийся подготовкой к ЕГЭ и ГИА по математике, могу сказать, что умение решать подобные задачи является ключевым при подготовке к Единому государственного экзамену по математике.

В данной статье мы кратко остановимся на основных проблемах, которые возникают у школьников при решении текстовых задач B13. Как обычно, будем разбирать все на примере конкретных задач B13, взятых из реальных вариантов ЕГЭ по математике прошлых лет. К каждому разобранному примеру в статье будет приведена аналогичная задача для самостоятельного решения для осуществления самоконтроля, без него никак. Тем не менее, если при их решении у вас возникнут какие-то вопросы, вы можете смело задавать их в комментариях. Ни один вопрос без ответа не останется.

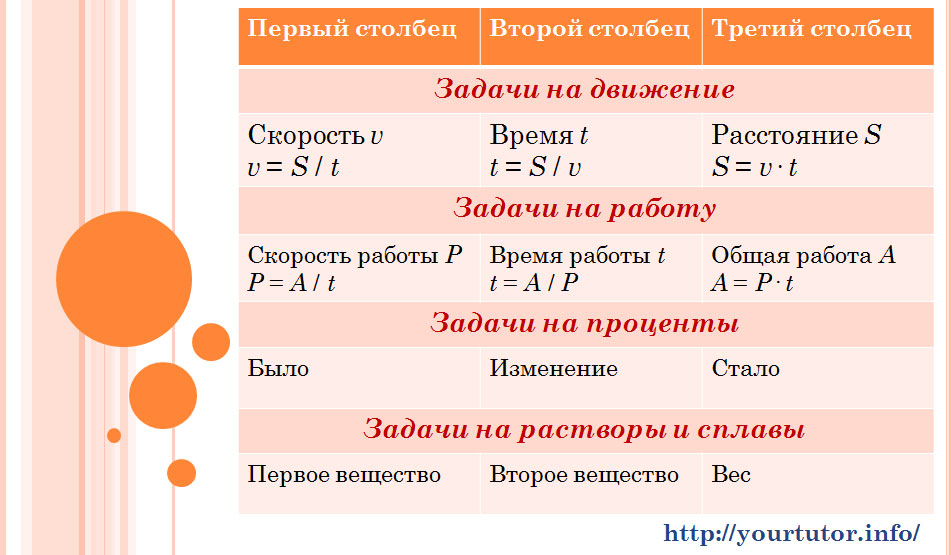
Прежде чем мы приступить к разбору конкретных текстовых задач B13, посмотрим, какие вообще существуют подходы к их решению. Наиболее распространенный и, надо сказать, довольно эффективный способ — использование таблиц. В зависимости от типа решаемой задачи (будь то задача на движение, работу, сплавы, растворы и проценты) столбики в этой таблице будут иметь разные названия:

Таблицы для решения текстовых задач B13 (задач на составление уравнений) из ЕГЭ по математике

Почему использование таких таблиц упрощает решение текстовых задач B13 на составление уравнений? Просто потому, что это удобно. Данные таблицы позволяют в наглядном и понятном виде записать условие задачи и провести его анализ для составления уравнения. Разберем это на конкретных примерах.

Текстовые задачи B13 на движение

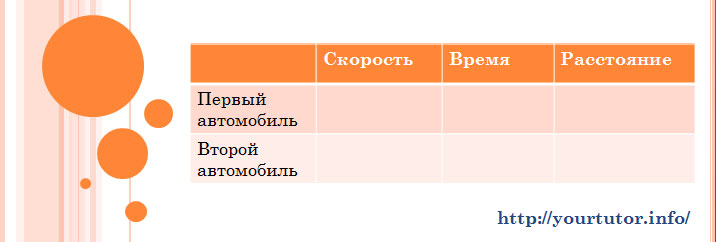
Решение. Итак, по шагам рассмотрим как заполняется таблица в данной задаче. Читаем текст задачи еще раз. Первое предложение: «Из пунктов A и B одновременно выехали навстречу друг другу два автомобиля.» Речь идет о двух автомобилях, значит наша таблица будет выглядеть следующим образом:

Внешний вид таблицы, используемой для решения текстовой задачи B13 на движение

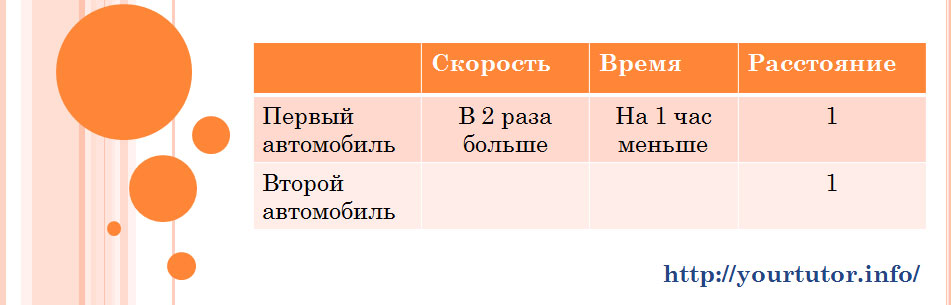
Читаем дальше. Второе предложение: «Первый автомобиль двигался в 2 раза быстрее второго и приехал в пункт B на 1 час раньше, чем второй приехал в пункт A.» В данном предложении, как видите, содержатся данные, которые нужно занести в соответствующие ячейки нашей таблицы. Фраза «он (первый автомобиль) приехал в пункт B на 1 час раньше, чем второй приехал в пункт A» означает, что время движения первого автомобиля было на 1 час меньше, чем второго. Попутно мы осознаем, что оба автомобиля проехали одинаковое расстояние, которое можно обозначить за 1. Заносим эти данные в таблицу, и она принимает вид:

Таблица для решения задачи b13 на движение с внесенными в нее данными

Для решения задачи нам нужно составить уравнение, следовательно, необходимо что-то обозначить за Формально за можно обозначить что угодно из того, что не известно. Задача в любом случае будет иметь решение. Просто при неудачном выборе возрастет сложность вычислений, а, соответственно, и вероятность ошибки. Наиболее простым уравнение получится в том случае, если за здесь обозначить скорость второго автомобиля. Вы можете легко убедиться в этом сами, выбрав какой-нибудь другой параметр и составив требуемое уравнение.

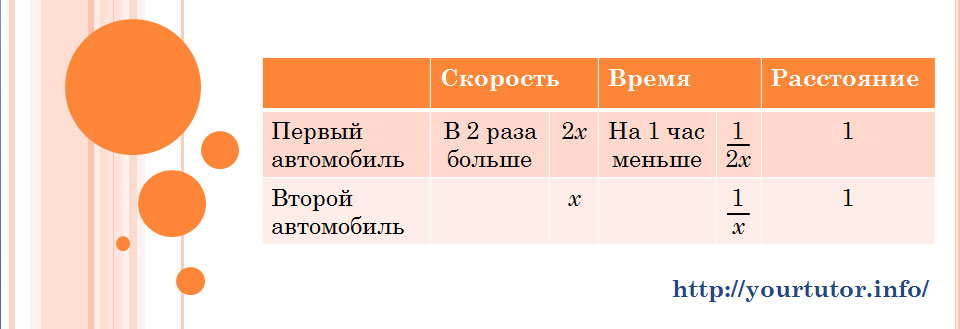
Итак, если скорость второго автомобиля то скорость первого автомобиля поскольку по условию она в 2 раза больше. Чтобы найти время движения, нужно расстояние разделить на скорость. То есть время движения второго автомобиля равно а время движения первого равно Заносим все эти данные в таблицу:

Заполненная таблица для решения текстовой задачи B13 на составление уравнения

Теперь написать уравнение для решения задачи не должно составить труда. Используем условие, что время движения первого автомобиля на 1 час меньше, чем второго:

То есть скорость движения второго автомобиля равна условных единиц в час. Тогда скорость движения первого автомобиля равна условная единица в час.

Напомню, что нам нужно определить: «На сколько минут раньше встретились бы автомобили, если бы скорость второго автомобиля была равна скорости первого?» Теперь, когда мы знаем скорости каждого автомобиля, мы без труда сможем ответить на этот вопрос.

Если бы второй автомобиль ехал с той же скорость, что и первый, то есть со скоростью 1 условная единица в час, то встреча произошла бы на середине пути через часа. Здесь 1 — полное расстояние, (1 + 1) — скорость сближения автомобилей.

На самом же деле встреча произошла через часа. Здесь, аналогично, 1 — полное расстояние, — скорость сближения автомобилей. То есть реально автомобили встретились позже на часа или на 10 минут.

Ответ: 10 минут.

Задача для самостоятельного решения №1. Из порта A в порт B отправился катер. Одновременно с ним из порта B в порт A отправилась моторная лодка. Катер прибыл в порт B на 2 часа быстрее, чем моторная лодка прибыла в порт A, а их встреча произошла через 45 минут после начала движения. Сколько часов двигалась моторная лодка из порта B в порт A?

Текстовые задачи B13 на работу

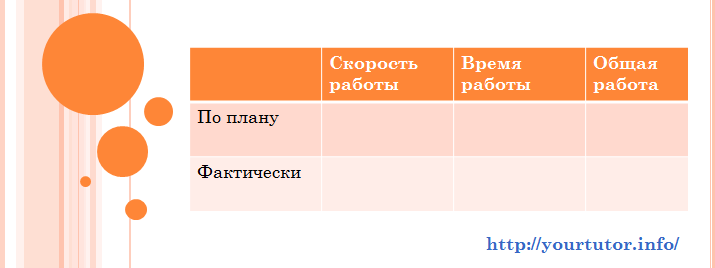
Решение. Читая условие, понимаем, что в задаче рассматриваются две ситуации: запланированная и произошедшая. Следовательно, наша таблица будет иметь следующий вид:

Внешний вид таблицы, используемой для решения текстовой задачи B13 из ЕГЭ по математике на работу

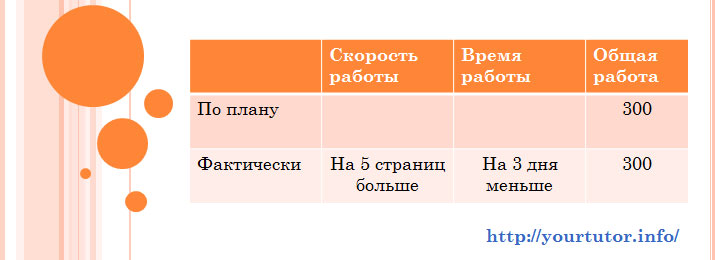
Читаем еще раз условие: «Писатель собрался напечатать на компьютере 300 страниц текста. Если бы он печатал на 5 страниц в день больше, чем запланировал, то смог бы завершить работу на 3 дня раньше.»

Скорость работы — это тот объем работы, который выполняется за единицу времени, в нашем случае — за один день. Следовательно, информация содержащаяся в высказывании «печатая на 5 страниц в день больше, чем запланировал», относится, очевидно, к фактической скорости работы.

Время работы — это то количество дней, которое понадобятся для выполнения всей работы. Следовательно, данные, содержащиеся в высказывании «он смог бы завершить работу на 3 дня раньше (чем запланировал)» относится к времени работы, причем к фактическому.

Общий же объем работы не зависит от планов нашего писателя и равен в том и в другом случае тремстам страницам. Заносим все эти данные в таблицу, и она в результате принимает вид:

Заполненная данными из условия таблица для решения задачи B13 на работу

Что здесь удобнее всего обозначить за То, что требуется найти, то есть скорость работы по плану. Так и сделаем. Раз скорость работы по плану равна то фактическая скорость работы равна потому что она по условию на 5 страниц в день больше.

Чтобы найти время работы, нужно общий объем работы разделить на скорость работы. То есть время работы по плану равно а фактическое время работы равно Снова занесем эти данные в таблицу, в результате чего она примет вид:

Таблица для составления уравнения для решения текстовой задачи B13 на работу

Теперь составить уравнение для решения задачи уже несложно. Используем то условие, что по факту работа была выполнена на 3 раньше запланированного срока. То есть запланированное время работы минус фактическое время работы равно трем дням:

Понятно, что отрицательный вариант нам не подходит. Итак, нас спрашивали: «Какое количество страниц в день запланировал печатать писатель?» Теперь мы можем ответить на этот вопрос. Наш писатель запланировал печатать по 20 страниц в день.

Ответ: 20.

Задача для самостоятельного решения №2. Время наполнения резервуара одной трубой на 22 минуты больше, чем второй. Если обе трубы будут работать вместе, они наполнят резервуар за один час. Сколько времени потребуется для наполнения резервуара одной второй трубой?

Текстовые задача B13 на проценты

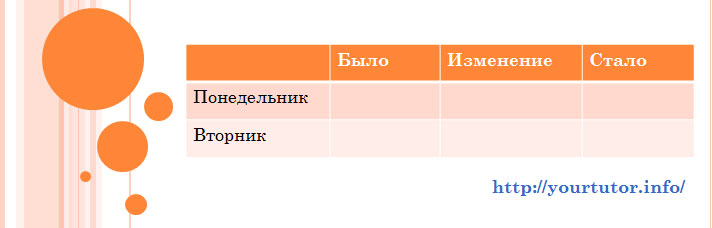
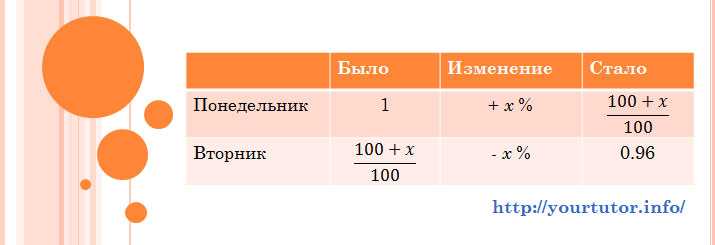
Решение. Итак, в понедельник акции поднялись в цене, во вторник — упали в цене. Для решения задачи нам потребуется таблица, содержащая помимо шапки две строки (для понедельника и вторника соответственно). То есть эта таблица будет иметь следующий вид:

Внешний вид таблицы для решения текстовой задачи B13 на проценты из ЕГЭ

Вопрос задачи: «На сколько процентов подешевели акции во вторник?» На это же количество процентов они подорожали в понедельник. Это мы и обозначим на неизвестную величину Поскольку нам не известна стоимость акций на момент открытия торгов в понедельник, примем ее за 1. Это никак не отразится на результате, ведь нам нужно определить лишь процентное изменение.

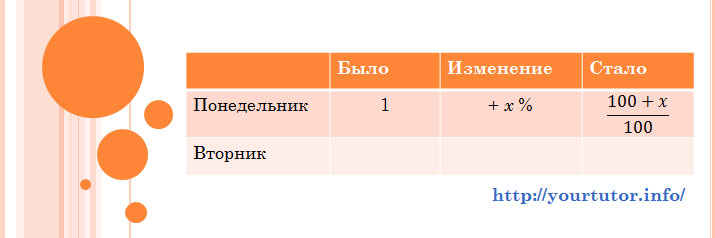
Итак, «в понедельник акции поднялись в цене на некоторое (в наших обозначениях ) количество процентов». Следовательно, после повышения их стоимость составила Заносим эту информацию в нашу таблицу.

Для тех, кому не понятно, откуда получилась такая формула, простой пример. Допустим футболка стоила 100 руб., потом ее цена увеличилась на 20%. Сколько стала стоить футболка? Каждый без труда ответит, что 120 руб. А как вы получили это значение? Умножили 100 на 1,2. А откуда вы взяли число 1,2? Из дроби где 20% — процент, на который повысилась стоимость футболки.

Частично заполненная таблица для решения текстовой задачи B13 на работу

Идем далее. «Во вторник упали в цене не то же самое количество процентов. В результате они оказались на 4% дешевле изначальной стоимости.» Итак, во вторник цена упала на процентов. Следовательно, новая цена стала равна Кому это не понятно, прочитайте еще раз пример с футболкой, описанный выше. При этом известно, что окончательная цена оказалась на 4% меньше первоначальной, равной 1, то  есть 0,96. Заносим эти данные в таблицу, после чего она принимает вид:

Заполненная таблица для решения текстовой задачи B13 на проценты

Теперь составить уравнение для решения задачи уже легко:

По смыслу задачи нам подходит только положительный ответ.

Ответ: 20.

Задача для самостоятельного решения №3. Цена покупки со скидкой в 4% составила 1152 рубля. Сколько стоила бы покупка без предоставления скидки?

Текстовые задачи B13 на сплавы

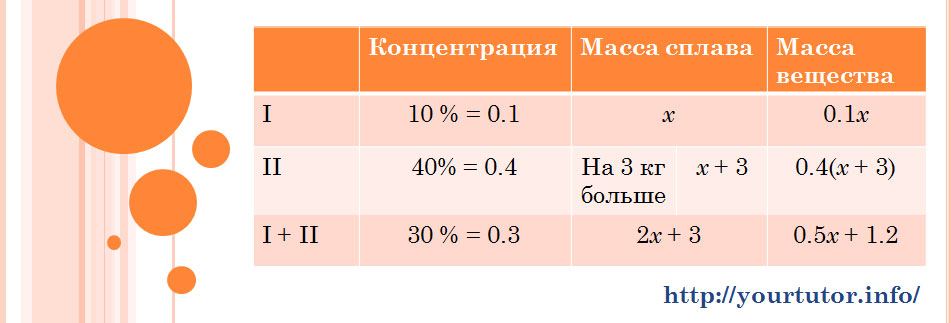
Решение. В задаче рассматриваются два сплава и третий сплав, состоящий из первых двух. Следовательно, в нашей таблице кроме шапки будет еще три строки (по одной на каждый из сплавов). То есть она будет иметь следующий вид:

Общий вид используемой для решения текстовой задачи B13 таблицы

Читаем еще раз условие: «Содержание меди в первом сплаве — 10%, содержание меди во втором сплаве — 40%. Второй сплав весит на 3 кг больше первого. Сплавив первые два сплава, получили третий сплав, содержание меди в котором оказалось 30%.» Все данные из условия заносим в соответствующие ячейки таблицы. Я думаю, вам не составит особого труда сделать это самостоятельно:

Частично заполненная таблица для решения текстовой задачи B13 на сплавы

Кажется, что в этой задаче удобнее всего за обозначить массу первого сплава. Тогда масса второго сплава будет А что такое «концентрация»? В данном случае под концентрацией понимается отношение массы вещества в сплаве к общей массе сплава. Следовательно, чтобы найти массу вещества (меди), нужно массу сплава умножить на соответствующую концентрацию, выраженную в виде десятичной дроби. Тогда содержание меди в первом сплаве равно а содержание меди во втором сплаве равно

Масса общего сплава, очевидно, будет равна сумме масс каждого из первоначальных сплавов, то есть Масса меди в общем сплаве тоже, очевидно, будет равна сумме масс меди в первом и во втором сплаве, то есть Вносим все эти данные в таблицу, и она принимает вид:

Заполненная таблица для решения текстовой задачи B13 на сплавы

Еще раз, концентрация — это отношение массы вещества в сплаве к массе сплава. Следовательно, чтобы узнать концентрацию получившегося сплава, нужно общую массу меди в третьем сплаве поделить на общую массу третьего сплава При этом из условия известно, что эта концентрация равна 30%. То есть уравнение для решения данной текстовой задачи B13 на сплавы будет иметь вид:

кг.

Это масса первого сплава. Тогда масса второго сплава равна кг. Читаем вопрос задачи: «Вычислите массу третьего сплава. Запишите ответ в килограммах.» Теперь мы располагаем достаточным количеством информации, чтобы дать правильный ответ. Масса третьего сплава равна кг.

Ответ: 9.

Задача для самостоятельного решения №4. После смешивания 4-х литров 15-процентного раствора вещества с таким же объемом 19-процентного раствора этого же вещества получили третий раствор. Вычислите концентрацию получившегося раствора.

Как репетитор по математике и физике рекомендую при решении текстовых задач B13 из ЕГЭ по математике внимательно читать вопрос задачи. Часто ученики в процессе решения забывают о том, что конкретно требуется найти. Поэтому прежде чем записывать что-либо в бланк ответов ЕГЭ, проверьте, о том ли вас спрашивают в задаче. Опыт показывает, что многие школьники испытывают трудности с составлением уравнений для решения текстовых задач B13. Но научиться их решать можно и нужно обязательно. Терять баллы на несложных заданиях из первой части ЕГЭ по математике всегда очень обидно. Удачи вам в подготовке и блестящих результатов на экзамене!

Репетитор физики и математики
Сергей Валерьевич