Чему равна сумма углов выпуклого многоугольника

В 8  классе на уроках геометрии в школе ученики впервые знакомятся с понятием выпуклого многоугольника. Очень скоро они узнают, что эта фигура обладает очень интересным свойством. Какой бы сложной она ни была, сумма всех внутренних и внешних углов выпуклого многоугольника принимает строго определенное значение. В данной статье репетитор по математике и физике рассказывает о том, чему равна сумма углов выпуклого многоугольника.

Сумма внутренних углов выпуклого многоугольника

Сумма внутренних углов выпуклого многоугольника равна , где — количество сторон многоугольника.

Как доказать эту формулу?

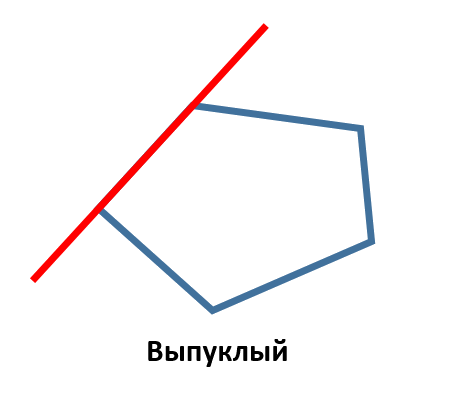
Прежде чем перейти к доказательству этого утверждения, вспомним, какой многоугольник называется выпуклым. Выпуклым называется такой многоугольник, который целиком находится по одну сторону от прямой, содержащей любую его сторону. Например такой, который изображен на этом рисунке:

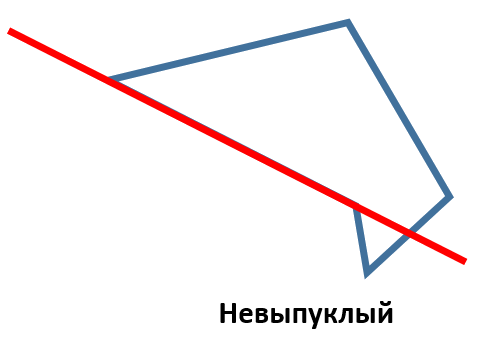
Если же многоугольник не удовлетворяет указанному условию, то он называется невыпуклым. Например, такой:

Сумма внутренних углов выпуклого многоугольника равна , где — количество сторон многоугольника.

Доказательство этого факта основано на хорошо известной всем школьникам теореме о сумме углов в треугольнике. Уверен, что и вам эта теорема знакома. Сумма внутренних углов треугольника равна .

Идея состоит в том, чтобы разбить выпуклый многоугольник на несколько треугольников. Сделать это можно разными способами. В зависимости от того, какой способ мы выберем, доказательства будут немного отличаться.

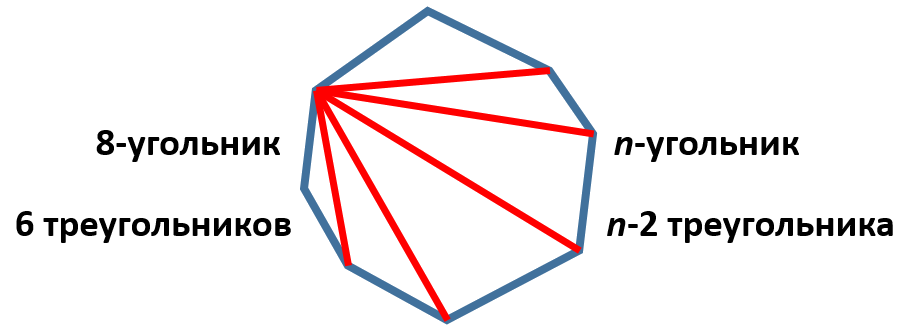
1. Разобьём выпуклый многоугольник на треугольники всеми возможными диагоналями, проведёнными из какой-нибудь вершины. Легко понять, что тогда наш n-угольник разобьётся на треугольника:

Причём сумма всех углов всех получившихся треугольников равна сумме углов нашего n-угольника. Ведь каждый угол в получившихся треугольниках является частичной какого-то угла в нашем выпуклом многоугольнике. То есть искомая сумма равна .

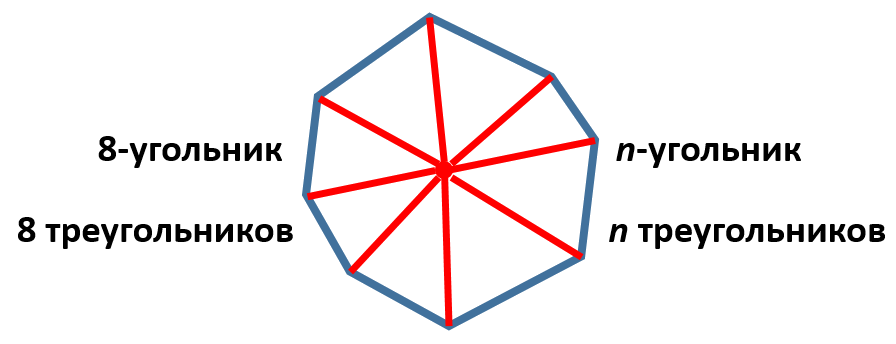
2. Можно также выбрать точку внутри выпуклого многоугольника и соединить её со всеми вершинами. Тогда наш n-угольник разобьется на треугольников:

Причём сумма углов нашего многоугольника в этом случае будет равна сумме всех углов всех этих треугольников за вычетом центрального угла, который равен . То есть искомая сумма опять же равна .

Сумма внешних углов выпуклого многоугольника

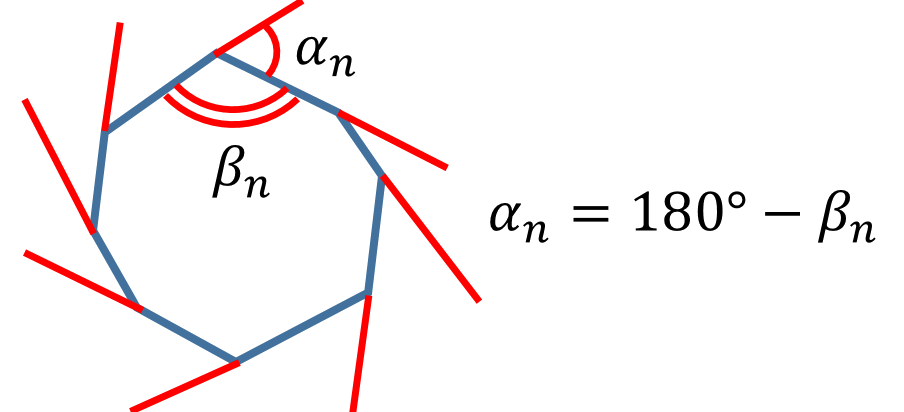
Зададимся теперь вопросом: «Чему равна сумма внешних углов выпуклого многоугольника?» Ответить на этот вопрос можно следующим образом. Каждый внешний угол является смежным с соответствующим внутренним. Поэтому он равен :

Тогда сумма всех внешних углов равна . То есть она равна .

То есть получается весьма забавный результат. Если отложить последовательно друг за другом все внешние углы любого выпуклого n-угольника, то в результате заполнится ровно вся плоскости.

Этот интересный факт можно проиллюстрировать следующим образом. Давайте пропорциональном уменьшать все стороны какого-нибудь выпуклого многоугольника до тех пор, пока он не сольётся в точку. После того, как это произойдёт, все внешние углы окажутся отложенными один от другого и заполнят таким образом всю плоскость.

Интересный факт, не правда ли? И таких фактов в геометрии очень много. Так что учите геометрию, дорогие школьники!

Материал о том, чему равна сумма углов выпуклого многоугольника, подготовил репетитор по геометрии, Сергей Валерьевич