В данной статье репетитор по математике и физике отвечает на вопрос, чему равен угол между биссектрисами смежных углов. Как оказалось, этот вопрос волнует многих школьников, которым предстоит сдавать ЕГЭ или ОГЭ по математике. Интересно то, что этот материал изучается в 7 классе, когда школьники только начинают своё знакомство с премудростями геометрии. Дочитайте эту статью до конца, и вы не только узнаете чему равен угол между биссектрисами смежных углов, но и поймёте, как это можно очень легко доказать.
Чему равен угол между биссектрисами смежных углов
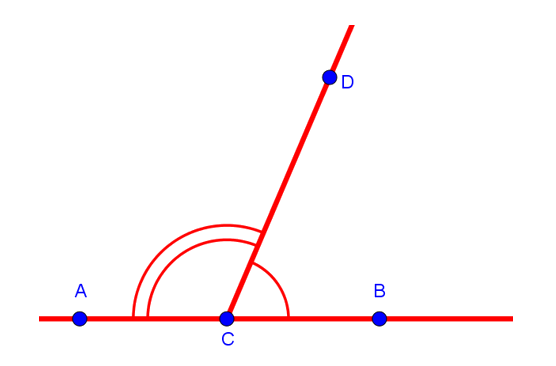
Начать нужно, конечно, с определения смежных углов. Смежными называются углы, которые как бы дополняют друг друга до развёрнутого. Проще всего продемонстрировать это с помощью рисунка. Если нарисовать прямую AB, отметить на ней между точками A и B точку C и провести из неё луч CD, то углы ACD и DCB будут являться смежными. На рисунке они отмечены одной и двумя дугами:
Ну и понятно, что поскольку смежные углы дополняют друг друга до развёрнутого угла, то в сумме они равны 
.
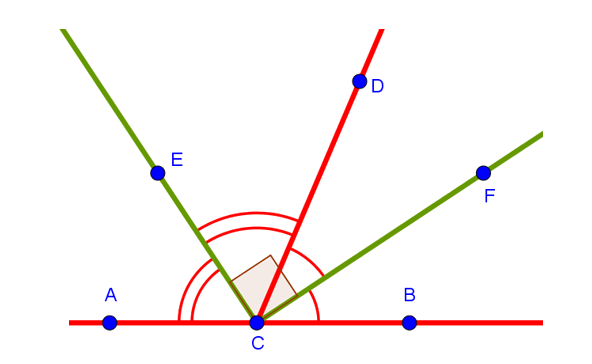
Проведём теперь биссектрисы этих смежных углов. Напомню, что биссектрисой называется «крыса, которая бегает по углам и делит угол пополам». Это такая запоминалочка для семиклассников, чтобы лучше запомнить. А если более строго, так сказать, по-научному, то биссектриса — это луч, исходящий из вершины угла и делящий его пополам. Ну и если нарисовать биссектрисы обоих углов (на рисунке снизу это зелёные линии CE и CF), то даже визуально заметно, что угол между ними составит 
:
Кто-то может мне возразить, сказав, что это случайно так получилось и что можно перерисовать рисунок так, что биссектрисы уже не будут взаимно перпендикулярны. Но нет! В том то и дело, что можно взять какие угодно смежные углы и угол между биссектрисами этих смежных углов обязательно будет прямым. Это удивительный факт, не правда ли?!
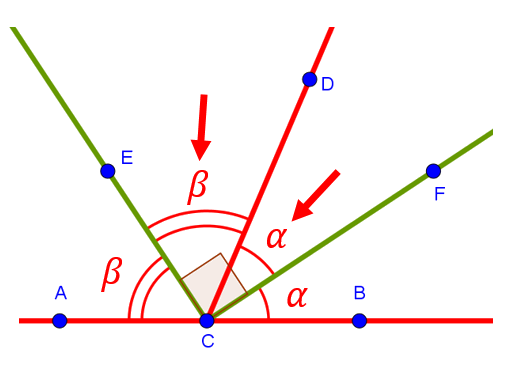
Но на самом деле, если вы уже были с ним раньше знакомы, то не на столько уж удивительный. Потому что на самом деле доказательство у этого факта довольно-таки простое. Обозначим равные углы FCB и DCF за 
, а равные углы DCE и ECA за 
:
Если посмотреть на рисунок, то все эти углы вместе образуют развёрнутый угол, то есть в сумме все они равны . То есть имеет место равенство:
![\[ 2\alpha + 2\beta = 180^{\circ}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-502409710ff7a1be4ac1ec011284c063_l3.png "Rendered by QuickLaTeX.com")
Если разделить обе части этого равенства на 2, то получится:
![\[ \alpha + \beta = 90^{\circ}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-2f070ca68f18d7de0f6ac207d573f4ae_l3.png "Rendered by QuickLaTeX.com")
То есть два уголочка в центре дают в сумме вне зависимости от величины каждого из этих углов. То есть угол ECF — прямой. Что и требовалось доказать.
Вот такой замечательный факт из элементарной геометрии. И таких фактов очень много. На своих занятиях я рассказываю о них своим ученикам. Помимо того, что это просто интересно, это ещё и очень пригодится в будущем при сдаче различных экзаменов по математике, в первую очередь ОГЭ и ЕГЭ.
Материал подготовил репетитор по математике, Сергей Валерьевич
2+2 =вопрос
2