При изучении тригонометрии в школе каждый ученик сталкивается с весьма интересным понятием «числовая окружность». От умения школьного учителя объяснить, что это такое, и для чего она нужна, зависит, насколько хорошо ученик поймёт тригонометрию впоследствии. К сожалению, далеко не каждый учитель может доступно объяснить этот материал. В результате многие ученики путаются даже с тем, как отмечать точки на числовой окружности. Если вы дочитаете эту статью до конца, то научитесь делать это без проблем.
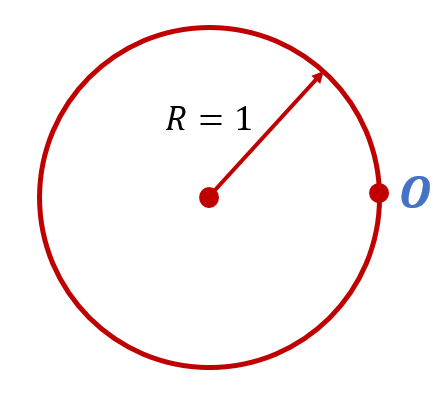
Итак, приступим. Нарисуем окружность, радиус которой равен 1. Самую «правую» точку этой окружности обозначим буквой O:
Поздравляю, вы только что нарисовали единичную окружность. Поскольку радиус этой окружности равен 1, то её длина равна ![]() .
.
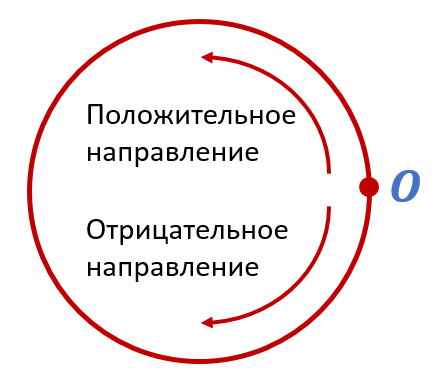
Каждому действительному числу можно поставить в соответствие длину траектории вдоль числовой окружности от точки O. За положительное направление принимается направление движения против часовой стрелки. За отрицательное – по часовой стрелке:
Расположение точек на числовой окружности
Как мы уже отмечали, длина числовой окружности (единичной окружности) равна ![]() . Где тогда будет располагаться на этой окружности число
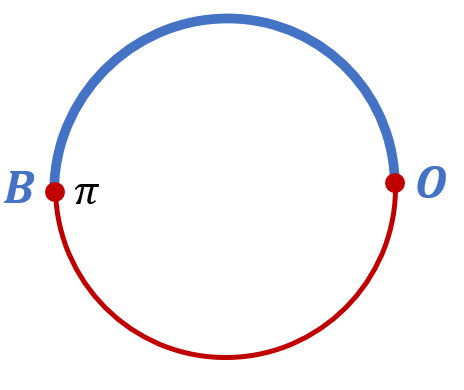
. Где тогда будет располагаться на этой окружности число ![]() ? Очевидно, от точки O против часовой стрелки нужно пройти половину длины окружности, и мы окажемся в нужной точке. Обозначим её буквой B:
? Очевидно, от точки O против часовой стрелки нужно пройти половину длины окружности, и мы окажемся в нужной точке. Обозначим её буквой B:
Обратите внимание, что в ту же точку можно было бы попасть, пройдя полуокружность в отрицательном направлении. Тогда бы мы отложили на единичной окружности число ![]() . То есть числам
. То есть числам ![]() и
и ![]() соответствует одна и та же точка.
соответствует одна и та же точка.
Причём этой же точке соответствуют также числа ![]() ,
, ![]() ,
, ![]() ,
, ![]() и, вообще, бесконечное множество чисел, которые можно записать в виде
и, вообще, бесконечное множество чисел, которые можно записать в виде ![]() , где
, где ![]() , то есть принадлежит множеству целых чисел. Всё это потому, что из точки B можно совершить «кругосветное» путешествие в любую сторону (добавить или вычесть длину окружности
, то есть принадлежит множеству целых чисел. Всё это потому, что из точки B можно совершить «кругосветное» путешествие в любую сторону (добавить или вычесть длину окружности ![]() ) и попасть в ту же самую точку. Получаем важный вывод, который нужно понять и запомнить.
) и попасть в ту же самую точку. Получаем важный вывод, который нужно понять и запомнить.
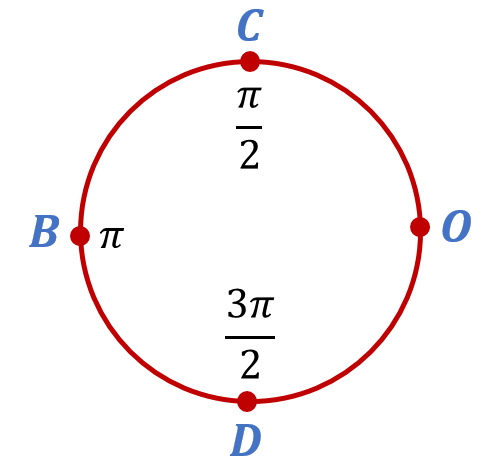
Разобьем теперь верхнюю полуокружность числовой окружности на дуги равной длины точкой C. Легко видеть, что длина дуги OC равна ![]() . Отложим теперь от точки C дугу той же длины в направлении против часовой стрелки. В результате попадём в точку B. Результат вполне ожидаемый, поскольку
. Отложим теперь от точки C дугу той же длины в направлении против часовой стрелки. В результате попадём в точку B. Результат вполне ожидаемый, поскольку ![]() . Отложим эту дугу в том же направлении ещё раз, но теперь уже от точки B. В результате попадём в точку D, которая будет уже соответствовать числу
. Отложим эту дугу в том же направлении ещё раз, но теперь уже от точки B. В результате попадём в точку D, которая будет уже соответствовать числу ![]() :
:
Заметим опять, что эта точка соответствует не только числу ![]() , но и, например, числу
, но и, например, числу ![]() , потому что в эту точку можно попасть, отложив от точки O четверть окружности в направлении движения часовой стрелки (в отрицательном направлении).
, потому что в эту точку можно попасть, отложив от точки O четверть окружности в направлении движения часовой стрелки (в отрицательном направлении).
И, вообще, отметим снова, что этой точке соответствует бесконечно много чисел, которые можно записать в виде ![]() . Но их также можно записать в виде
. Но их также можно записать в виде ![]() . Или, если хотите, в виде
. Или, если хотите, в виде ![]() . Все эти записи абсолютно равнозначны, и они могут быть получены одна из другой.
. Все эти записи абсолютно равнозначны, и они могут быть получены одна из другой.
Разобьём теперь дугу на OC пополам точкой M. Сообразите теперь, чему равна длина дуги OM? Правильно, вдвое меньше дуги OC. То есть ![]() . Каким числам соответствует точка M на числовой окружности? Уверен, что теперь вы сообразите, что эти числа можно записать в виде
. Каким числам соответствует точка M на числовой окружности? Уверен, что теперь вы сообразите, что эти числа можно записать в виде ![]() .
.
Но можно и иначе. Давайте в представленной формуле возьмём ![]() . Тогда получим, что
. Тогда получим, что ![]() . То есть эти числа можно записать в виде
. То есть эти числа можно записать в виде ![]() . Этот же результат можно было получить, используя числовую окружность. Как я уже говорил, оба записи равнозначны, и они могут быть получены одна из другой.
. Этот же результат можно было получить, используя числовую окружность. Как я уже говорил, оба записи равнозначны, и они могут быть получены одна из другой.
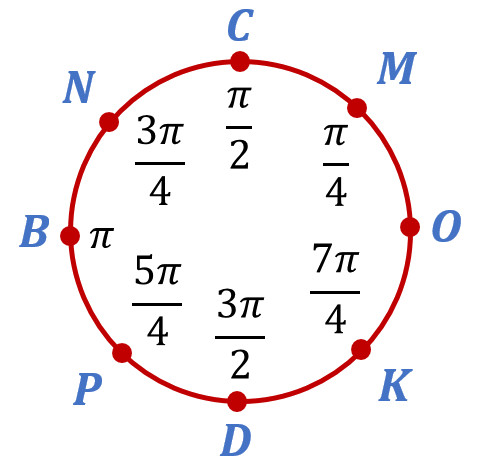
Теперь вы легко можете привести пример чисел, которым соответствуют точки N, P и K на числовой окружности. Например, числам ![]() ,
, ![]() и
и ![]() :
:
Часто именно минимальные положительные числа и берут для обозначения соответствующих точек на числовой окружности. Хотя это совсем не обязательно, и точке N, как вы уже знаете, соответствует бесконечное множество других чисел. В том числе, например, число ![]() .
.
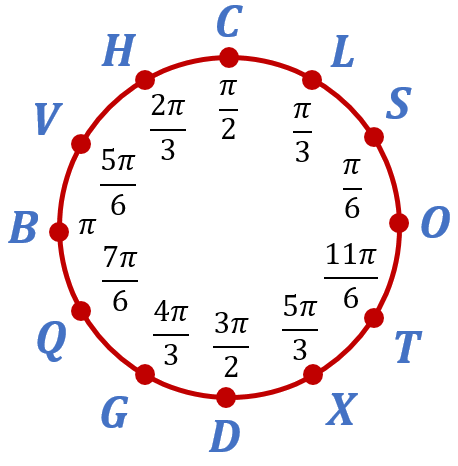
Если разбить дугу OC на три равные дуги точками S и L, так что точка S будет лежать между точками O и L, то длина дуги OS будет равна ![]() , а длина дуги OL будет равна
, а длина дуги OL будет равна ![]() . Используя знания, которые вы получили в предыдущей части урока, вы без труда сообразите, как получились остальные точки на числовой окружности:
. Используя знания, которые вы получили в предыдущей части урока, вы без труда сообразите, как получились остальные точки на числовой окружности:
Числа не кратные π на числовой окружности
Зададимся теперь вопросом, где на числовой прямой отметить точку, соответствующую числу 1? Чтобы это сделать, надо от самой «правой» точки единичной окружности O отложить дугу, длина которой была бы равна 1. Указать место искомой точки мы можем лишь приблизительно. Поступим следующим образом.
Мы знаем, где на числовой прямой находится точка L, соответствующая числу ![]() . Мы также знаем приблизительное значение числа
. Мы также знаем приблизительное значение числа ![]() . Тогда, очевидно, число
. Тогда, очевидно, число ![]() чуть больше 1. Следовательно, точка, которая соответствует числу 1, расположена на числовой окружности чуть ближе к точке O, чем точка L:
чуть больше 1. Следовательно, точка, которая соответствует числу 1, расположена на числовой окружности чуть ближе к точке O, чем точка L:
Отмеченной точке, как мы уже знаем, соответствуют также числа ![]() .
.
Таким образом, на сегодняшнем уроке мы усвоили, что каждому числу соответствует какая-то точка на числовой окружности, но каждой точке числовой окружности соответствует бесконечное множество чисел. Запомните это, чтобы не путаться в дальнейшем при изучении тригонометрии.
Надеюсь, вы усвоили этот урок. Чтобы убедиться в этом, выполните самостоятельно следующие упражнения. Возникшие вопросы обсудим с вами в комментариях:
- Выделите на числовой окружности дугу, все точки которой удовлетворяют условию:
![]()
- Как расположены точки на числовой окружности, соответствующие числам:
a) ![]() и
и ![]() ;
;
б) ![]() и
и ![]() ;
;
в) ![]() и
и ![]() ;
;
г) ![]() и
и ![]() ?
?
Материал подготовил репетитор по физике и математике в Москве, Сергей Валерьевич


Вроде что-то начало проясняется, но очень смутно,..
Спасибо за объяснение!
все точки соответствующим числам t и минус t совпадают а точки t +π расположены на противоположной стороне числового круга
Норм так, но мне не понятно( -_-)
очень смутно, что то было понятно, но в целом -нет. Но все равно спасибо.
«объяснить, что это такое, и для чего она нужна, зависит, насколько хорошо ученик пойдём тригонометрию впоследствии.»
Так куда мы пойдём с этой тригонометрией?