До сдачи ЕГЭ по математике остается все меньше времени. Обстановка накаляется, нервы у школьников, родителей, учителей и репетиторов натягиваются все сильнее. Снять нервное напряжение вам помогут ежедневные углубленные занятия по математике. Ведь ничто, как известно, так не заряжает позитивом и не помогает при сдаче экзаменов, как уверенность в своих силах и знаниях. Сегодня репетитор по математике расскажет вам о решении систем логарифмических и показательных неравенств, заданий, традиционно вызывающих трудности у многих современных старшеклассников.
Для того, чтобы научиться решать задачи C3 из ЕГЭ по математике как репетитор по математике рекомендую вам обратить внимание на следующие важные моменты.
1. Прежде чем приступить к решению систем логарифмических и показательных неравенств, необходимо научиться решать каждый из этих типов неравенств в отдельности. В частности, разобраться с тем, как находится область допустимых значений, проводятся равносильные преобразования логарифмических и показательных выражений. Некоторые связанные с этим тайны вы сможете постичь, изучив статьи «Решение задач C3 ЕГЭ по математике — логарифмические уравнения и неравенства» и «Решение задач C3 ЕГЭ по математике с репетитором — показательные уравнения и неравенства».
2. При этом необходимо осознавать, что решение системы неравенств не всегда сводится к решению отдельно каждого неравенства и пересечению полученных промежутков. Иногда, зная решение одного неравенства системы, решение второго значительно упрощается. Как репетитор по математике, занимающийся подготовкой школьников к сдаче выпускных экзаменов в формате ЕГЭ, раскрою в этой статье парочку связанных с этим секретов.
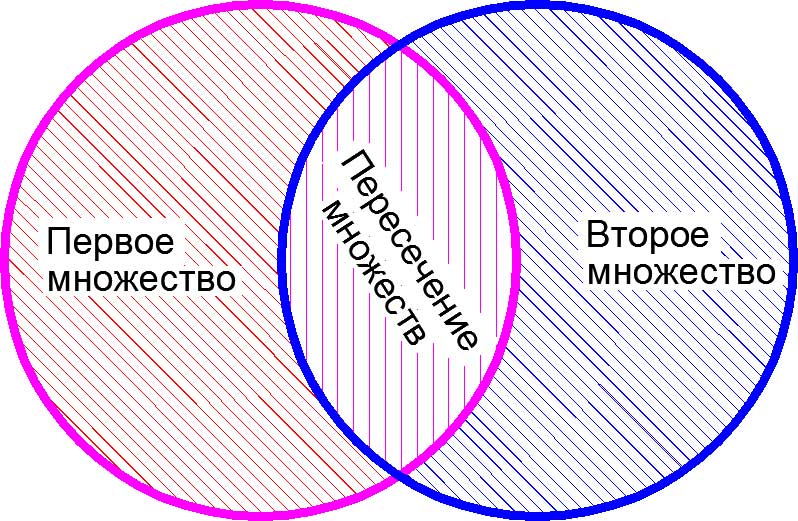
3. Необходимо четко уяснить для себя разницу между пересечением и объединением множеств. Это одно из важнейших математических знаний, которое опытный профессиональный репетитор старается дать своему ученику уже с первых занятий. Наглядное представление о пересечении и объединении множеств дают так называемые «круги Эйлера».
Другими словами, если даны два множества ![]() и
и ![]() то их пересечением будет являться множество следующего вида:
то их пересечением будет являться множество следующего вида: ![]()
Объяснение на пальцах. У Дианы в сумочке находится «множество», состоящее из {ручки, карандаша, линейки, тетрадки, расчески}. У Алисы в сумочке находится «множество», состоящее из {записной книжки, карандаша, зеркальца, тетрадки, котлеты по-киевски}. Пересечением этих двух «множеств» будет «множество», состоящее из {карандаша, тетрадки}, поскольку оба этих «элемента» есть и у Дианы, и у Алисы.
![Rendered by QuickLaTeX.com \[ \begin{cases}f(x)\lor 0, \\ g(x)\lor 0;\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-a1429c9842d75b45a5e44d12a0cbac1f_l3.png)
является промежуток ![]() то есть пересечение исходных промежутков. Здесь и далее под
то есть пересечение исходных промежутков. Здесь и далее под ![]() подразумевается любой из знаков
подразумевается любой из знаков ![]() а под
а под ![]() — ему противоположный знак.
— ему противоположный знак.
Другими словами, если даны два множества ![]() и
и ![]() то их объединением будет являться множество следующего вида:
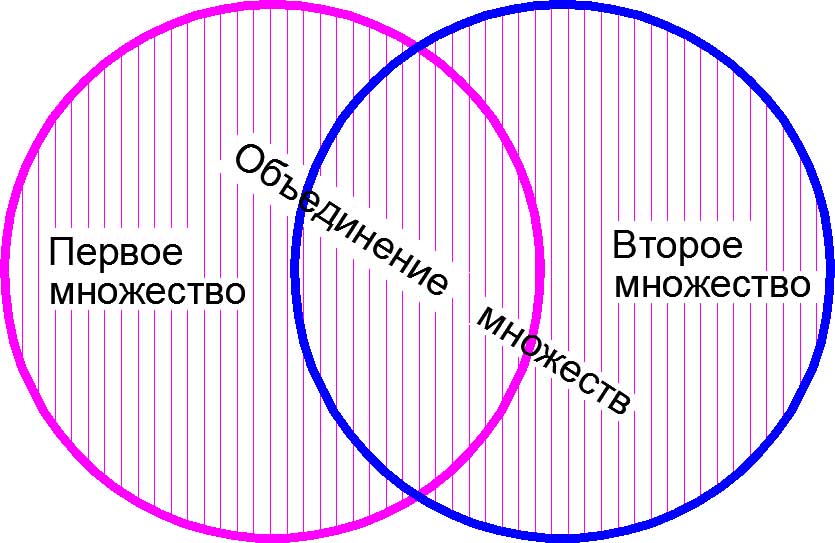
то их объединением будет являться множество следующего вида: ![]()
Объяснение на пальцах. Объединением «множеств», взятых в предыдущем примере будет «множество», состоящее из {ручки, карандаша, линейки, тетрадки, расчески, записной книжки, зеркальца, котлеты по-киевски}, поскольку оно состоит из всех элементов исходных «множеств». Одно уточнение, которое может оказаться не лишним. Множество не может содержать в себе одинаковых элементов.
![]()
является промежуток ![]() то есть объединение исходных промежутков.
то есть объединение исходных промежутков.
Перейдем непосредственно к примерам.
![Rendered by QuickLaTeX.com \[ \begin{cases}4^x-6\cdot 2^x+8\geqslant 0, \\ \log_3\frac{2x^2+3x-5}{x+1}\leqslant 1.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-618fb81789e0544e15fa165c6bacea8b_l3.png)
Решение задачи C3.
1. Решаем сперва первое неравенств. Используя замену ![]() переходим к неравенству:
переходим к неравенству:
![]()
Переходим к обратной подстановке:
![]()
![]()
2. Решаем теперь второе неравенство. Область его допустимых значений определяется неравенством:
![]()
В области допустимых значений с учетом того, что основание логарифма ![]() переходим к равносильному неравенству:
переходим к равносильному неравенству:
![]()
![]()
Исключая решения, не входящие в область допустимых значений, получаем промежуток ![]()
3. Ответом к системе неравенств будет пересечение полученных промежутков, то есть ![]()
![Rendered by QuickLaTeX.com \[ \begin{cases} 2^x+16\cdot 2^{-x}\geqslant 17, \\ 2\log_9(4x^2+1)\leqslant \log_3(3x^2+4x+1).\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8548250d1c0b9356f11adf84d8e0922c_l3.png)
Решение задачи C3.
1. Решаем сперва первое неравенство. Умножаем обе части на ![]() и делаем замену
и делаем замену ![]() в результате чего приходим к неравенству:
в результате чего приходим к неравенству:
![]()
Переходим к обратной подстановке:
![]()
![]()
2. Решаем теперь второе неравенство. Область его допустимых значений определяется системой:
![Rendered by QuickLaTeX.com \[ \begin{cases}4x^2+1>0, \\ 3x^2+4x+1>0\end{cases}\Leftrightarrow x\in(-\mathcal{1};-1)\cup\left(-\frac{1}{3};+\mathcal{1}\right). \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-1623c1e9fdb715693917447cac1f0ab0_l3.png)
Воспользовавшись свойствами логарифмов, в области допустимых значений переходим к равносильному неравенству:
![]()
![]()
Данный промежуток целиком входит в область допустимых значений данного неравенства.
3. Общее решение системы будет являться пересечением полученных промежутков, то есть ![]()
![Rendered by QuickLaTeX.com \[ \begin{cases}3^x<1+12\cdot 3^{-x}, \\ 2\operatorname{ln}\frac{1}{3x-2}+\operatorname{ln}(5-2x)\geqslant 0.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-16083effe92028efb86dee60b134bf8f_l3.png)
Решение задачи C3.
1. Решаем сперва первое неравенство. Умножаем обе его части на ![]() после чего получаем неравенство:
после чего получаем неравенство:
![]()
Используя подстановку ![]() переходим к следующему неравенству:
переходим к следующему неравенству:
![]()
Переходим к обратной подстановке:
![]()
2. Решаем теперь второе неравенство. Определим сначала область допустимых значений этого неравенства:
![Rendered by QuickLaTeX.com \[ \begin{cases} \frac{1}{3x-2}>0, \\ 5-2x>0 \end{cases}\Leftrightarrow \begin{cases}x>\frac{2}{3}, \\ x<2,5\end{cases}\Leftrightarrow x\in\left(\frac{2}{3}; 2,5\right). \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-d104372fe264cb6aea226ed781d6e3ba_l3.png)
В области допустимых значений переходим к равносильному неравенству:
![]()
![Rendered by QuickLaTeX.com \[ \frac{9x^2-10x-1}{(3x-2)^2}\leqslant 0\Leftrightarrow x\in\left[\frac{5-\sqrt{34}}{9};\frac{5+\sqrt{34}}{9}\right]. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-1a98483d3d4669bed2f35092a21c171a_l3.png)
Обращаем внимание, что
![]()
![]()
Тогда с учетом области допустимых значений получаем: ![]()
3. Находим общее решения неравенств. Сравнение полученных иррациональных значений узловых точек — задача в данном примере отнюдь не тривиальная. Сделать это можно следующим образом. Так как
![]()
![]()
то ![]() и окончательный ответ к системе имеет вид:
и окончательный ответ к системе имеет вид: ![]()
![Rendered by QuickLaTeX.com \[ \begin{cases}\log_{\log_x 3x}(4x-1)\geqslant 0, \\ 21^x-9\cdot 7^x-3^x+9\leqslant 0.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-fb046136dcb68ffaf8c338c85007e2ac_l3.png)
Решение задачи С3.
1. Решим сперва второе неравенство:
![]()
![]()
![]()
2. Первое неравенство исходной системы представляет собой логарифмическое неравенство с переменным основанием. Удобный способ решения подобных неравенств описан в статье «Сложные логарифмические неравенства», в его основе лежит простая формула:
![]()
![]()
Вместо знака ![]() может быть подставлен любой знак неравенства, главное, чтобы он был один и тот же в обоих случаях. Использование данной формулы существенно упрощает решение неравенства:
может быть подставлен любой знак неравенства, главное, чтобы он был один и тот же в обоих случаях. Использование данной формулы существенно упрощает решение неравенства:
![]()
![]()
![]()
Определим теперь область допустимых значений данного неравенства. Она задается следующей системой:
![Rendered by QuickLaTeX.com \[ \begin{cases}4x-1>0, \\ \log_x 3x > 0, \\ \log_x 3x\ne 1, \\ x> 0, \\ x\ne 1\end{cases}\Leftrightarrow \begin{cases}x>\frac{1}{4}, \\ \log_x 3x >\log_x 1, \\ x\ne 1, \\ x>0, \\ x\ne 1\end{cases}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-2ba5c4ed7557c6157358ef55049384d5_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}x>\frac{1}{4}, \\ (3x-1)(x-1)>0 \\ x>0, \\ x\ne 1\end{cases}\Leftrightarrow x\in\left(\frac{1}{4};\frac{1}{3}\right)\cup(1;+\mathcal{1}). \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-690ce9750fcd4c2232a9a081e35372c5_l3.png)
Легко видеть, что одновременно этот промежуток будет являться и решением нашего неравенства.
3. Окончательным ответом исходной системы неравенств будет пересечение полученных промежутков, то есть ![]()
![Rendered by QuickLaTeX.com \[ \begin{cases}25^x-30\cdot 5^x+125\geqslant 0,\\ \log_x(x-1)\cdot \log_x(x+1)\leqslant 0.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ecbacf8a2c52636e6590a83a133ff0d9_l3.png)
Решение задания C3.
1. Решаем сперва первое неравенство. Используем подстановку ![]() Переходим к следующему квадратному неравенству:
Переходим к следующему квадратному неравенству:
![]()
2. Решаем теперь второе неравенство. Область его допустимых значений определяется системой:
![Rendered by QuickLaTeX.com \[ \begin{cases}x>0, \\ x\ne 1, \\ x-1>0, \\ x+1 > 0\end{cases}\Leftrightarrow x\in(1;+\mathcal{1}). \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-14cd8ee02fdbcc07b1d0275959553213_l3.png)
Данное неравенство равносильно следующей смешанной системе:
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\begin{cases}\log_x(x-1)\leqslant 0, \\ \log_x(x+1)\geqslant 0,\end{cases} \\ \begin{cases}\log_x(x-1)\geqslant 0, \\ \log_x(x+1)\leqslant 0.\end{cases}\end{array}\right. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-bef775e1b15a488c7ef69585ce010546_l3.png)
В области допустимых значений, то есть при ![]() используя равносильные преобразования переходим к следующей смешанной системе:
используя равносильные преобразования переходим к следующей смешанной системе:
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\begin{cases} x-1\leqslant 1, \\ x+1\geqslant 1,\end{cases} \\ \begin{cases}x-1\geqslant 1, \\ x+1\leqslant 1.\end{cases}\end{array}\right.\Leftrightarrow\left[\begin{array}{l}\begin{cases} x\leqslant 2, \\ x\geqslant 0,\end{cases} \\ \begin{cases}x\geqslant 2, \\ x\leqslant 0.\end{cases}\end{array}\right.\Leftrightarrow x\in[0;2]. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-9d199fa007abade7a5ee756e249a188d_l3.png)
С учетом области допустимых значений получаем: ![]()
3. Окончательным решением исходной системы является пересечение полученных промежутков, то есть ![]()
Изображение полученных промежутков на числовой прямой
![Rendered by QuickLaTeX.com \[ \begin{cases}\frac{3\cdot 64^x+2^x-70}{64^x-2}\geqslant 3, \\ \log_3^2(x+3)-3\log_3(x+3)+2\leqslant 0.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-3fe0ca27e7c88ff3303c295d8705b742_l3.png)
Решение задачи C3.
1. Решаем сперва первое неравенство. Равносильными преобразованиями приводим его к виду:
![]()
![]()
2. Решаем теперь второе неравенство. Область его допустимых значений определяется промежутком: ![]() Используя замену переменной
Используя замену переменной ![]() переходим к следующему квадратичному неравенству:
переходим к следующему квадратичному неравенству:
![]()
![]()
Этот ответ целиком принадлежит области допустимых значений неравенства.
3. Пересечением полученных в предыдущих пунктах промежутков получаем окончательный ответ к системе неравенств: ![]()
Сегодня мы с вами решали системы логарифмических и показательных неравенств. Задания подобного рода предлагались в пробных вариантах ЕГЭ по математике в течение всего ныне идущего учебного года. Однако, как репетитор по математике, имеющий опыт подготовки к ЕГЭ, могу сказать, что это вовсе не означает, что аналогичные задания будут в реальных вариантах ЕГЭ по математике в июне.
Позволю себе высказать одно предостережение, адресованное в первую очередь репетиторам и школьным учителям, занимающимся подготовкой старшеклассников к сдаче ЕГЭ по математике. Весьма опасно готовить школьников к экзамену строго по заданным темам, ведь в этом случае возникает риск полностью «завалить» его даже при незначительном изменении ранее заявленного формата заданий. Математическое образование должно быть полным. Уважаемые коллеги, пожалуйста, не уподобляйте роботам своих учеников так называемым «натаскиванием» на решение определенного типа задач. Ведь нет ничего хуже формализации мышления человека.
Всем удачи и творческих успехов!
Профессиональный репетитор по физике и математике
Сергей Валерьевич
© Народная мудрость


Большое спасибо! Мне действительно помогла эта статья! Я, конечно, и раньше понимал, как решать эту ересь, но то решал, то не решал. А сейчас все отлично! Еще раз благодарю!
Уважаемый Сергей Валерьевич!
Спасибо за возможность задать вопрос.
Есть ли способ решения системы трёх логарифмических уравнений с тремя неизвестными?
Аналитический или иной.
Т.Петров
Добрый день. Численные методы решения безусловно есть всегда, какой бы сложной ни была система. Вопрос только во времени вычислений. Ну а аналитический способ тоже может быть. Здесь нужно рассматривать каждый конкретный пример отдельно.