Часто решению задач по геометрии на уроках в школе уделяется недостаточно внимания. Связано это с тем, что в ЕГЭ по математике заданий по планиметрии всего три, два из которых элементарны, а третье — задача C4, до которой на экзамене добирается редкий школьник. Кроме того, решение задач по геометрии не предполагает действий по определенному алгоритму (чему научить значительно проще), в отличие от многих заданий по алгебре и началам анализа, предлагаемых в ЕГЭ. Вот и возникает ситуация, когда в ущерб решению задач по планиметрии, школьные преподаватели предпочитают, скажем, задачи на нахождение наибольшего или наименьшего значения функций.
Между тем пользы от умения решать сложные задачи по геометрии не меньше, чем от знания тех же основ математического анализа. Освоить приемы решения задач C4 должен каждый ученик одиннадцатого класса, если он хочет сдать предстоящий экзамен на отлично. В данной статье мы продолжаем разбор заданий C4 из сборника типовых тестовых задач ЕГЭ по математике 2012.
Вариант 2. В трапеции ABCD известны боковые стороны AB = 27, CD = 28 и верхнее основание BC = 5. Известно, что ![]() Найдите AC.
Найдите AC.
Решение:
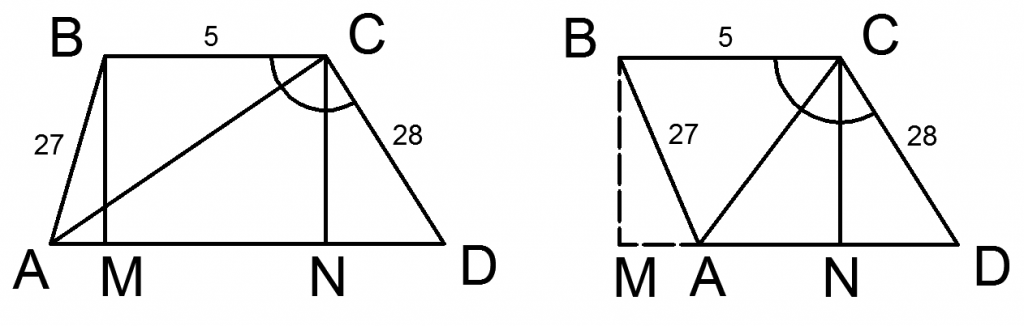
Возможны два случая, изображенные на рисунке. Рассмотрим отдельно каждый:
1) Случай на левом рисунке. CN и BM — высоты трапеции. Поскольку ∠NDC = 1800 — ∠BCD (углы являются соответствующими при параллельных прямых BC, AD и секущей CD), то по формулам приведения cos ∠NDC = -cos ∠BCD = 2/7, sin ∠NDC = 3√5/7. Из прямоугольного треугольника CND имеем: CN = CD sin ∠NDC = 12√5. AM находим по теореме Пифагора для прямоугольного треугольника ABM: AM2 = AB2 — BM2 = 729 — 720 = 9 или AM = 3. Значит AN = AM + MN = 8. AC теперь находим по теореме Пифагора для прямоугольного треугольника ACN: AC2 = AN2 + CN2 = 64 + 720 = 784 или AC = 28.
2) Случай, изображенный на правом рисунке, аналогичен предыдущему. Разница лишь в том, что AN = MN — AM = BC — AM = 2. Значит AC2 = AN2 + CN2 = 4 + 720 = 724 или AC = 2√181.
Ответ: 28 или 2√181.
Вариант 4. Окружности с центрами O1 и O2 пересекаются в точках A и B. Известно, что ∠AO1B = 900, ∠AO2B = 600, O1O2 = a. Найдите радиусы окружностей.
Решение:
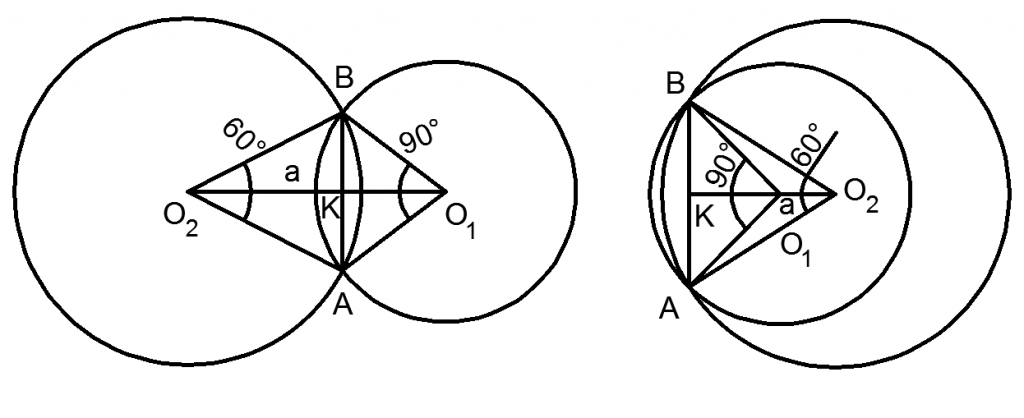
В зависимости от взаимного расположения окружностей возможны два случая:
1) Случай, изображенный на левом рисунке. Треугольник O2BA равнобедренный (две его боковые стороны являются радиусами левой окружности), поэтому углы при его основании равны, то есть ∠O2BK = ∠O2AK. Тогда прямоугольные треугольники O2BK и O2AK (доказательство того, что они действительно прямоугольные, читайте в статье «Задачи на доказательство геометрических фактов из ГИА» — задача 11) равны по гипотенузе и острому углу, поэтому ∠BO2K = ∠AO2K = 300. В прямоугольном треугольнике O2BK против угла BO2K, равного 300, лежит катет BK = R2/2 (*). По теореме Пифагора для этого треугольника O2K = √3R2/2. Прямоугольный треугольник O1BK является равнобедренным, поэтому O1K = BK = √2R1/2, откуда с учетом равенства (*) получаем связь R1 и R2: R2 = √2R1. С учетом того, что O1K + O2K = a, получаем: √2R1/2 + √6R1/2 = a, окончательно R1 = a√2/(√3+1), R2 = 2a/(√3+1).
2) Случай, изображенный на правом рисунке. Ситуация аналогична, разница заключается лишь в том, что в данном случае a = O2K — O1K. Ответы в этом случае таковы: R1 = a√2/(√3-1), R2 = 2a/(√3-1).
Ответ: R1 = a√2/(√3+1), R2 = 2a/(√3+1) или R1 = a√2/(√3-1), R2 = 2a/(√3-1).
Вариант 9. Основания трапеции равны a и b. Прямая, параллельная основаниям, разбивает трапецию на две трапеции, площади которых относятся как 2 : 3. Найдите длину отрезка этой прямой, заключенного внутри трапеции.
Решение:
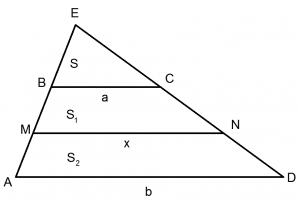
Дополнительное построение: продолжим боковые стороны трапеции до пересечения (см. рисунок). Пусть S — площадь треугольника BEC, S1 — площадь трапеции MBCN, S2 — площадь трапеции AMND. Возможны два случая:
1) Пусть S1 : S2 = 2 : 3 или S2 = 1.5 S1. Площади подобных треугольников, как известно, относятся как квадрат коэффициента подобия. Тогда из подобия треугольников BCE и ADE:
Из подобия треугольников MEN и AED:
Тогда:
2) В случае, когда S2 : S1 = 2 : 3 или S1 = 1.5 S2, получаем абсолютно аналогично:
Что и будет являться ответом.
Умение решать задачи по геометрии, предлагаемые во второй части вариантов ЕГЭ по математике, приходит со временем. Это не тот случай, когда требуется отработать и в дальнейшем использовать какой-то универсальный алгоритм, применимый для решения целого класса типовых заданий. Однако, научится решать задачи C4 по силам каждому школьнику. Успехов вам в подготовке и блестящих результатов на экзамене!
Репетитор по математике
Сергей Валерьевич


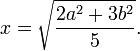
Вариант 2
cos ∠NDC = 2/7
sin ∠NDC = 3√5/7
Откуда тройка, если Sin2(a)=1-Cos2(a), а далее корень из 1-косинус в квадрате. Если подставить «наши» числа, то sin=корень(1-2/7), приводим к общему знаменателю и получаем Sin = корень(5/7)
Вы же сами говорите «корень из 1-косинус в квадрате», а пишите без квадрата. sin=корень(1-(2/7)^2) = корень((49-4)/49) = 3корня_из5/7.
Спасибо, в следующей задаче: откуда берется что BK=R/2? И почему можно однозначно предположить что прямая O1O2 делить угол в 60 градусов пополам?
O1K = BK = √2R1/2
откуда взялось это?
Потому что O1BK прямоугольный и равнобедренный (два угла по 45 градусов), а BK и KO1 — боковые стороны.
Ну вообще это, конечно, доказывать надо.
Треугольник O2BA равнобедренный (две его боковые стороны являются радиусами левой окружности), поэтому углы при его основании равны, то есть ∠O2BK = ∠O2AK. Тогда прямоугольные треугольники O2BK и O2AK равны по гипотенузе и острому углу, поэтому ∠BO2K = ∠AO2K = 30 градусов.
«Потому что O1BK прямоугольный и равнобедренный (два угла по 45 градусов), а BK и KO1 — боковые стороны.»
И что это нам дает? Ни одну из сторон мы не знаем, значит теорему пифагора здесь не применить. А что еще тут можно, я даже не знаю
Извините, на счет r/2 понял
Я имею ввиду откуда взялось √2R1/2, а не само равенство
К примеру, это можно получить, расписав синус 45 градусов для этого треугольника: sin 45 = BK/R1 = √2/2, откуда всё и получается.
Все понял, спасибо
R1 = a√2/(√3+1) нельзя ли подробней?
Ну тут простые преобразования:
√2R1/2 + √6R1/2 = a или R1(√2/2 + √6/2) = a или R1(√2 + √6)/2 = a откуда R1 = 2a/(√2 + √6) далее выносим √2 в знаменателе: R1 = 2a/(√2(1 + √3)) и сокращаем на него.
Почему треугольники BO2K и АО2К прямоугольные?
Задачи на доказательство геометрических фактов
Задача №11.
Спасибо огромное!
Большое спасибо за понятное объяснение 🙂
Выручили!)
Не понимаю, как решается система в 9 варианте, можно пояснить?
Можно. Из первого уравнения выражается S1/S. Оно равно x^2/a^2 — 1. Затем подставляется во второе уравнение. Получается 1+2.5*(x^2/a^2 — 1)=b^2/a^2. Далее раскрываются скобки и выражается значение x.
спасибо вам большое! 🙂