В задании 13 ЕГЭ по математике профильного уровня требуется решить уравнение и осуществить отбор его корней, удовлетворяющих некоторому условию. В данной статье представлен разбор такого задания из профильного уровня ЕГЭ по математике, предложенного в 2016 году. Доступен видеоразбор решения от репетитора по математике.
| а) Решите уравнение:
б) Укажите корни этого уравнения, принадлежащие отрезку |
Видеоразбор задания доступен здесь:
а) Используем замену ![]() . Тогда уравнение принимает вид:
. Тогда уравнение принимает вид:
![]()
Дискриминант данного уравнения равен:
![]()
Тогда корни уравнения равны:
![Rendered by QuickLaTeX.com \[ t_{1,2} = \frac{-b\pm\sqrt{D}}{2a} = \left[ \begin{array}{l} t_1 = \frac{-(-7)-\sqrt{25}}{2\cdot 2} \\ t_2 = \frac{-(-7)+\sqrt{25}}{2\cdot 2}. \end{array} = \left[ \begin{array}{l} t_1 = \frac{1}{2} \\ t_2 = 3. \end{array} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ed2a8299cbc1acb970e935f06d10d4ac_l3.png)
Обратная подстановка приводит к следующему результату:
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l} \log_2\left(2\sin x\right) = \frac{1}{2} \\ \log_2\left(2\sin x\right) = 3 \end{array}\Leftrightarrow \left[\begin{array}{l} 2\sin x = 2^{\frac{1}{2}} \\ 2\sin x = 2^3 \end{array}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e4aa5ca00322a6e4a349f84fe7bb62a1_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l} 2\sin x = \sqrt{2} \\ 2\sin x = 8 \end{array}\Leftrightarrow \left[\begin{array}{l} \sin x = \frac{\sqrt{2}}{2} \\ \sin x = 4. \end{array} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e758d60c3369000899cb2889886090fd_l3.png)
Второе уравнение не имеет корней, поскольку ![]() . Решением второго уравнения является серия:
. Решением второго уравнения является серия:
![Rendered by QuickLaTeX.com \[ x = (-1)^n\cdot\textrm{arcsin}\left(\frac{\sqrt{2}}{2}\right)+\pi n,\, n\in Z. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ad7cc7e3652febe72febc02422997f2b_l3.png)
Получаем следующую серию:
![]()
Эту серию можно записать иначе:
![]()
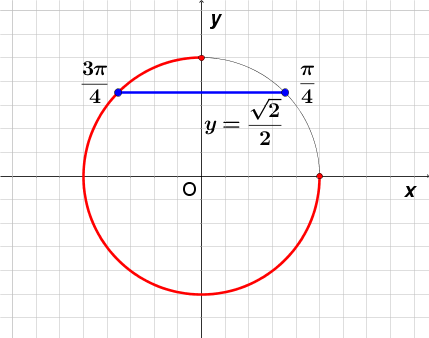
б) Осуществляем отбор решений с помощью единичной окружности. На рисунке множество ![]() выделено красным цветом:
выделено красным цветом:
Из рисунка видно, что подходит только один корень: ![]() .
.
Ответ: а) ![]() ,
,
б) ![]() .
.
Репетитор по математике в Москве, Сергей Валерьевич

АААА СЛООЖНАААА!!!!!!
ЛЕГКО
Помоги!!!
нет
чего нет?
не легко решить, если не знаешь формул
красиво!
это пример того как НЕЛЬЗЯ оформлять задание. нет ОДЗ, на рис не указаны промежутки.
Здесь нет ни одного неравносильного преобразования, поэтому указывать здесь ОДЗ не имеет ни малейшего смысла. Промежуток выделен на рисунке красным цветом.
дауны, это изи
нифига подобного
Зачем все это? ЗАЧЕМ???
ну уж точно не затем, чтобы научиться писать…