Решение задач C4 из ЕГЭ по математике (начало)

Времени до экзамена остается все меньше, пробные ЕГЭ проводятся все чаще, нервы у школьников и их учителей натягиваются все сильнее. В преддверии открытия сезона «интенсивной подготовки» к выпускным и вступительным экзаменам предлагаю вам потренироваться в решении задач C4 из пособия «ЕГЭ-2012. Математика. Типовые тестовые задания», разработанного МИОО для подготовки школьников к ЕГЭ по математике. Задачи приведены с решениями, однако, полезно было бы решить их сперва самостоятельно.

Вариант 3. Треугольник ABC вписан в окружность радиуса 12. Известно, что AB = 6 и BC = 4. Найдите AC.

Решение:

Из теоремы синусов для треугольника ABC имеем:

Из основного тригонометрического тождества находим, что:

Тогда по теореме косинусов для треугольника ABC имеем для обоих случаев:

Ответ: √35 ± √15.

Вариант 5. В треугольнике ABC проведены высоты BM и CN , O — центр вписанной окружности. Известно, что BC = 24 , MN = 12. Найдите радиус окружности, описанной около треугольника BOC .

Решение:

Возможны два случая:

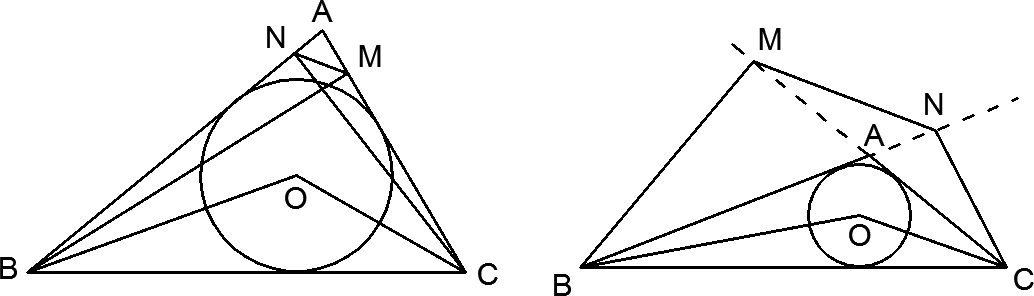
1) Пусть ∠A — острый (левый рисунок). Докажем, что треугольники AMN и ABC подобны. Действительно, точки B, N, M и C лежат на окружности с диаметром BC, следовательно, ∠NMB = ∠NCB, из прямоугольных треугольников BAM и BNC:
∠AMN = 90⁰  — ∠NMB, ∠B = 90⁰  — ∠NCB, из чего, очевидно, следует вывод, что ∠AMN = ∠B, кроме того ∠A — общий для обоих треугольников, следовательно, они подобны по двум углам.

Из прямоугольного треугольника AMB: cos∠A = AM/AB, из прямоугольного треугольника ANC: cos∠A = AN/AC. Эти же отношения являются, очевидно, соотношениями сторон в подобных треугольниках AMN и ABC, из чего следует, что cos∠A = NM/BC = 1/2, а значит ∠A = 60⁰, Поскольку сумма углов в треугольнике равна 180⁰, ∠B + ∠C  = 120⁰. Центр вписанной в треугольник окружности лежит, как известно, в точке пересечения его биссектрис. Из этого делаем вывод, что:
∠OBC+∠OCB = 1/2 · (∠B + ∠C)  = 60⁰, а значит ∠BOC = 120⁰. По теореме синусов для треугольника BOC имеем: BC/sin∠BOC = 2R, где R — искомый радиус описанной около треугольника окружности. Отсюда: R = 8√3.

2) Пусть теперь ∠A — тупой (правый рисунок). Из прямоугольного треугольника ABM находим, что cos∠BAM = AM/AB, из прямоугольного треугольника CAN находим, что cos∠CAN = AN/AC.  ∠BAM = ∠CAN, так как они вертикальные, значит AM/AB = AN/AC = cos∠BAM = cos∠BAС, так как два последних угла смежные. Значит треугольники ABC и ANM подобны по углу и двум пропорциональным сторонам. Коэффициент подобия равен cos∠BAС = MN/BC = -1/2, а сам угол ∠BAС = 120⁰.

Дальнейшие рассуждения аналогичны. Поскольку сумма углов в треугольнике равна 180⁰, ∠B + ∠C  = 60⁰. Центр вписанной в треугольник окружности лежит в точке пересечения его биссектрис, поэтому:
∠OBC + ∠OCB = 1/2 · (∠B + ∠C)  = 30⁰, а значит ∠BOC = 150⁰. По теореме синусов для треугольника BOC имеем: BC/sin∠BOC = 2R, где R — искомый радиус описанной около треугольника окружности. Отсюда: R = 24.

Ответ: 8√3 или 24.

Вариант 8. Периметр равнобедренной трапеции равен 52. Известно, что в эту трапецию можно вписать окружность, причем боковая сторона делится точкой касания в отношении 4 : 9. Прямая, проходящая через центр окружности и вершину трапеции, отсекает от трапеции треугольник. Найдите отношение площади этого треугольника к площади трапеции.

Решение:

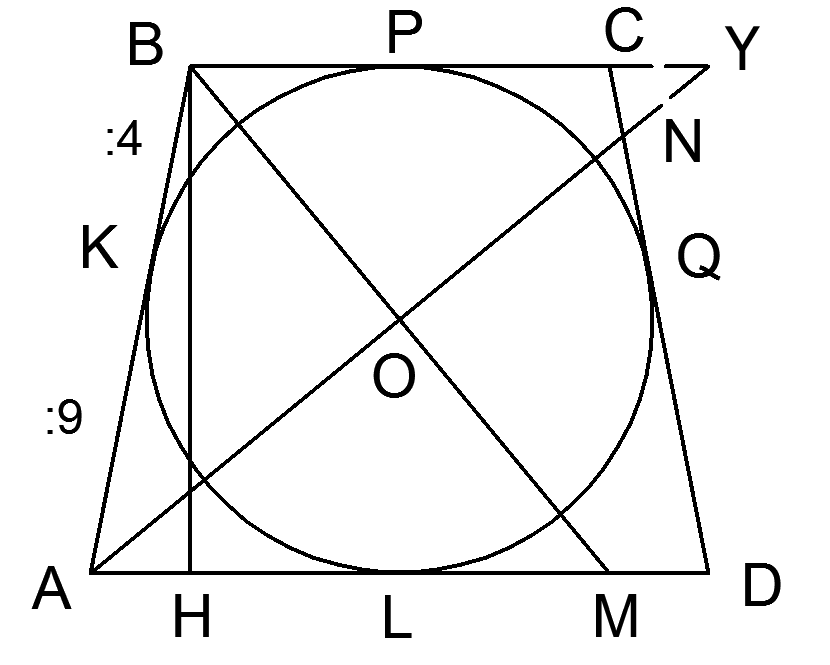
По теореме об отрезках касательных KB = BP = PC = CQ = 4x, QD = DL = LA = AK = 9x, тогда периметр трапеции равен 4 · (9x + 4x) = 52, откуда x = 1. Отсюда вычисляем боковые стороны AB = CD = 13 и основания BC = 8, AD = 18. Тогда AH = (AD — BC)/2 = 5. Из прямоугольного треугольника BHA по теореме Пифагора находим высоту трапеции BH = 12, sin∠A = sin∠D = 12/13. Площадь трапеции тогда равна S = (BC + AD) · BH/2 = 156.

В зависимости от того, о какой прямой говорится в условии задачи, возможны два случая:

1) Пусть данная прямая проходит через вершину, содержащую меньшее основание трапеции (на рисунке прямая BM). Центр вписанной в угол окружности лежит на его биссектрисе, то есть ∠ABM = ∠MBC, ∠MBC = ∠AMB (как накрест лежащие при параллельных прямых BC, AD и секущей BM), значит ∠ABM = ∠AMB и треугольник ABM — равнобедренный, AM = AB = 13. Тогда площадь треугольника ABM = 0.5 · AB · AM · sin∠A  = 0.5 · 13 · 13 · 12/13 = 78, а искомое отношение равно 78/156 = 1/2.

2) Пусть теперь прямая, о которой говорится в условии, проходит через вершину, содержащую меньшее основание трапеции (на рисунке прямая AN). Выполним дополнительное построение: продлим основание BC и прямую AN до пересечения в точке Y. Аналогично доказываем, что треугольник ABY — равнобедренный, AB = BY = 13, CY = BY — BC = 5. Треугольники CNY и AND подобны по двум углам (∠AND = ∠CNY как вертикальные, ∠CYA = ∠YAD как накрест лежащие при параллельных прямых BC, AD и секущей AY), значит DN : NC = AD : CY = 18 : 5, значит DN = 18/23 CD = 18/23 AB = 234/23. Тогда площадь треугольника ADN = 0.5 · AD · DN · sin∠D  = 0.5 · 18 · 234/23 · 12/13 = 1944/23, а искомое отношение равно 162/299.

Ответ: 1/2 или 162/299.

Репетитор математики и физики
Сергей Валерьевич