Резонанс в цепи переменного тока

Автор

Четверг, 21 января, 2016

В данной статье рассказано о явлении резонанса в цепи переменного тока, состоящей из катушки, конденсатора и активного сопротивления, соединенных последовательно. Введены понятия резонансной частоты, добротности контура, а также разобраны соответствующие примеры задач из ЕГЭ по физике.

Явление резонанса в цепи переменного тока

Явление резонанса в контуре, состоящем из последовательно соединённых катушки индуктивности L, конденсатора C и активного сопротивления R, заключается в резком возрастании амплитуды вынужденных колебаний силы тока при совпадении циклической частоты \omega генерируемой источником переменной ЭДС e(t) с собственной циклической частотой \omega_0 электромагнитных колебаний в контуре:

Rendered by QuickLaTeX.com

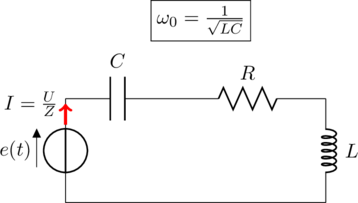
Напомним, что частота переменного тока \nu связана с циклической частотой переменного тока \omega простым соотношением:

    \[ \omega = 2\pi\nu. \]

Цепь, состоящую из катушки индуктивности, конденсатора и активного сопротивления, соединённых последовательно, сокращенно называют RLC-цепью. Резонанс в RLC-цепи возникает при такой циклической частоте \omega_0, что реактивное сопротивление катушки X_L = \omega_0 L становится равным по модулю реактивному сопротивлению конденсатора X_C = \frac{1}{\omega_0 C}. Поскольку эти составляющие импеданса RLC-цепи отстоят друг от друга по фазе на \pi (колеблются в противофазе), то компенсируют друг друга, в результате полное сопротивление цепи Z = \sqrt{R^2+\left(X_L - X_C\right)^2 становится наименьшим, а действующее значение сила тока I = \frac{U}{Z} — наибольшим (здесь U — действующее значение напряжения, генерируемого источником переменной ЭДС):

    \[ \begin{cases} X_C = \frac{1}{\omega_0 C}, \\ X_L = \omega_0 L, \\ X_C = X_L, \\ Z = \sqrt{R^2+\left(X_L - X_C\right)^2}. \end{cases} \Leftrightarrow \begin{cases} \omega_0 = \frac{1}{\sqrt{LC}}, \\ Z = R. \end{cases} \]

Векторная диаграмма для случая резонанса в цепи переменного тока, состоящей из катушки, конденсатора и активного сопротивления, соединенных последовательно, имеет вид:

Rendered by QuickLaTeX.com

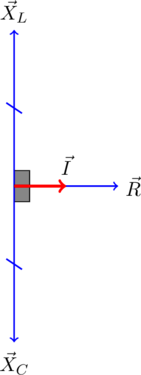
Добротность RLC-цепи

Резонансные цепи используют для того, чтобы выделить сигнал на нужной частоте, отфильтровав остальные сигналы на других частотах. Если отложить по вертикали действующее значение силы тока вынужденных колебаний в RLC-контуре, а по горизонтали — частоту генерируемой источником переменной ЭДС, то получится резонансная кривая данного RLC-контура, подобная той, что изображена на рисунке:

Rendered by QuickLaTeX.com

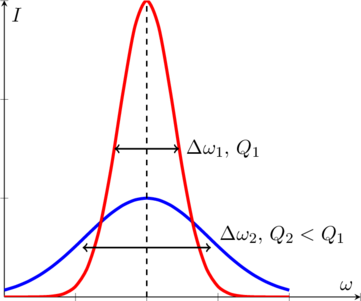
Если резонансная кривая имеет острый пик на резонансной частоте, говорят, что схема обладает высокой «селективностью». Параметр, характеризующий данное свойство, в физике называют добротностью Q. Добротность RLC-контура определяется как отношение его резонансной частоты \omega_0 к ширине резонансной полосы на полувысоте максимума \Delta\omega:

    \[ Q = \frac{\omega_0}{\Delta\omega}. \]

Добротность RLC-цепи зависит от величины активного сопротивления. Чем меньше активное сопротивление R, тем больше добротность при данных значениях индуктивности L и электроемкости C. Для RLC-контура добротность определяется по формуле:

    \[ Q = \frac{1}{R}\sqrt{\frac{L}{C}}. \]

Задача из ЕГЭ по физике про резонанс в цепи переменного тока

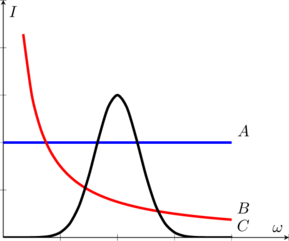
При под­клю­че­нии трех не­из­вест­ных эле­мен­тов A, B и C элек­три­че­ской цепи к вы­хо­ду ге­не­ра­то­ра пе­ре­мен­но­го тока с из­ме­ня­е­мой ча­сто­той гар­мо­ни­че­ских ко­ле­ба­ний при не­из­мен­ной ам­пли­ту­де ко­ле­ба­ний на­пря­же­ния, об­на­ру­же­ны следующие зависимости действующих значений силы тока от ча­сто­ты:

Rendered by QuickLaTeX.com

Установите соответствие между буквой графика и соответствующим элементом из списка, который был подключен:

1) активное сопротивление
2) кон­ден­са­то­р
3) ка­туш­ка
4) RLC-контур

A B C
 A
  • Правильный ответ для графика A — 1 (активное сопротивление), поскольку из представленных в списке элементов лишь активное сопротивление не имеет зависимости от частоты в цепи переменного тока.
  • Правильный ответ для графика B — 2 (катушка), поскольку индуктивное сопротивление катушки возрастает пропорционально частоте переменного тока. Тогда действующее значение силы переменного тока уменьшается обратно пропорционально частоте.
  • Правильный ответ для графика B — 4 (RLC-контур), так как на кривой зависимости действующего значения силы переменного тока от частоты имеется ярко выраженный резонансный максимум, что является характерным признаком RLC-контура.

Материал подготовлен репетитором по физике на Юго-Западной, сергеем Валерьевичем

Метки: , , , , ,
Опубликовано в категории Методическая копилка | 2 комментария »

Комментарии

  1. Анатолий:
    04.09.2022 в 03:50

    Цикл = период. Поэтому циклическая частота то же, что и периодическая, измеряется в герцах. А частота ω= 2πf называется круговой, обозначает количество радиан, а не циклов, за секунду.
    И на графике кривые сопротивления, тока и добротности токовой цепи, а не «RLС-контур»

    Ответить
    1. Сергей Валерьевич:
      04.09.2022 в 07:06

      Цикл ≠ период. Период — это вообще время (одного полного колебания). Термин «циклическая частота» вводится, например, в пособии Г.Я. Мякишев, А.З. Синяков «Колебания и волны», с. 11. Обозначение «RLC-контур» также очень распространено, а главное, намного более содержательно, чем «токовая цепь».

      Ответить

Добавить комментарий