В данной статье репетитор по физике и математике рассказывает о том, как рассчитать перегрузку, которую испытывает тело в момент разгона или торможения. Данный материал очень плохо рассматривается в школе, поэтому школьники очень часто не знают, как осуществлять расчёт перегрузки, а ведь соответствующие задания встречаются на ЕГЭ и ОГЭ по физике. Так что дочитайте эту статью до конца или посмотрите прилагающийся видеоурок. Знания, которые вы получите, пригодятся вам на экзамене.
Начнём с определений. Перегрузкой называется отношение веса тела к величине силы тяжести, действующей на это тело у поверхности земли. Вес тела — это сила, которая действует со стороны тела на опору или подвес. Обратите внимание, вес — это именно сила! Поэтому измеряется вес в ньютонах, а не в килограммах, как некоторые считают.
Таком образом, перегрузка — это безразмерная величина (ньютоны делятся на ньютоны, в результате ничего не остаётся). Однако, иногда эту величину выражают в ускорениях свободного падения. Говорят, к примеру, что перегрузка равна 
, имея ввиду, что вес тела вдвое больше силы тяжести.
Примеры расчёта перегрузки
Покажем, как осуществлять расчёт перегрузки на конкретных примерах. Начнём с самых простых примеров и перейдём далее к более сложным.
| Пример 1. Чему равна перегрузка человека, стоящего на земле? Чему равна перегрузка человека, свободно падающего с некоторой высоты? |
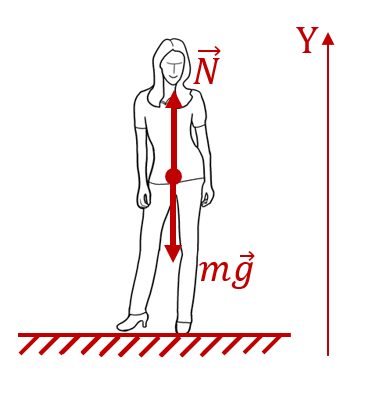
Очевидно, что человек, стоящий на земле, не испытывает никаких перегрузок. Поэтому хочется сказать, что его перегрузка равна нулю. Но не будем делать поспешных выводов. Нарисуем силы, действующие на этого человека:
К человеку приложены две силы: сила тяжести 
, притягивающая тело к земле, и противодействующая ей со стороны земной поверхности сила реакции 
, направленная вверх. На самом деле, если быть точным, то эта сила приложена к подошвам ног человека. Но в данном конкретном случае, это не имеет значения, поэтому её можно отложить от любой точки тела. На рисунке она отложена от центра масс человека.
Вес человека 
приложен к опоре (к поверхности земли), в ответ в соответствии с 3-м законом Ньютона со стороны опоры на человека действует равная по величине и противоположно направленная сила . Значит для нахождения веса тела, нам нужно найти величину силы реакции опоры.
Поскольку человек стоит на месте и не проваливается сквозь землю, то силы, которые на него действуют скомпенсированы. То есть 
, и, соответственно, 
. То есть расчёт перегрузки в этом случае даёт следующий результат:
![\[ \frac{P}{mg} = \frac{mg}{mg} = 1. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-30c6b72fcb234535995262bea256f512_l3.png "Rendered by QuickLaTeX.com")
Запомните это! При отсутствии перегрузок перегрузка равна 1, а не 0. Как бы странно это не звучало.
Определим теперь, чему равна перегрузка человека, который находится в свободном падении.
Если человек пребывает в состоянии свободного падения, то на него действует только сила тяжести, которая ничем не уравновешивается. Силы реакции опоры нет, как нет и веса тела. Человек находится в так называемом состоянии невесомости. В этом случае перегрузка равна 0.
| Пример 2. Определите перегрузку космонавтов, находящихся в ракете, движущейся на небольшой высоте вверх с ускорением 40 м/с2. |
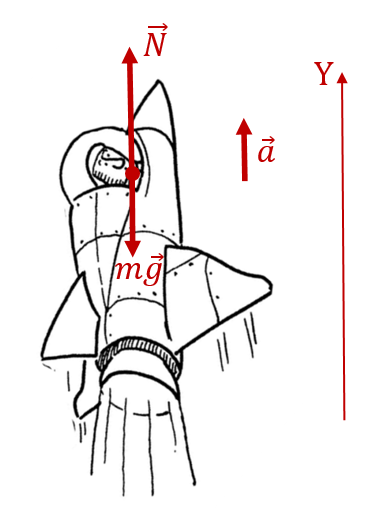
Космонавты находятся в горизонтальном положении в ракете во время её старта. Только так они могут выдержать перегрузки, которые они испытывают, не потеряв при этом сознания. Изобразим это на рисунке:
В этом состоянии на них действует две силы: сила реакции опоры и сила тяжести . Как и в прошлом примере, модуль веса космонавтов равен величине силы реакции опоры: 
. Отличие будет состоять в том, что сила реакции опоры уже не равна силе тяжести, как в прошлый раз, поскольку ракета движется вверх с ускорением 
. С этим же ускорением синхронно с ракетой ускоряются и космонавты.
Тогда в соответствии со 2-м законом Ньютона в проекции на ось Y (см. рисунок), получаем следующее выражение: 
, откуда 
. То есть искомая перегрузка равна:
![\[ \frac{P}{mg} = \frac{m(a+g)}{mg} = \frac{a+g}{g} = \frac{40+10}{10} = 5. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e9a9a6b267fc1ab6bd7f1028cc516fe4_l3.png "Rendered by QuickLaTeX.com")
Надо сказать, что это не самая большая перегрузка, которую приходится испытывать космонавтам во время старта ракеты. Перегрузка может доходить до 7. Длительное воздействие таких перегрузок на тело человека неминуемо приводит к летальному исходу.
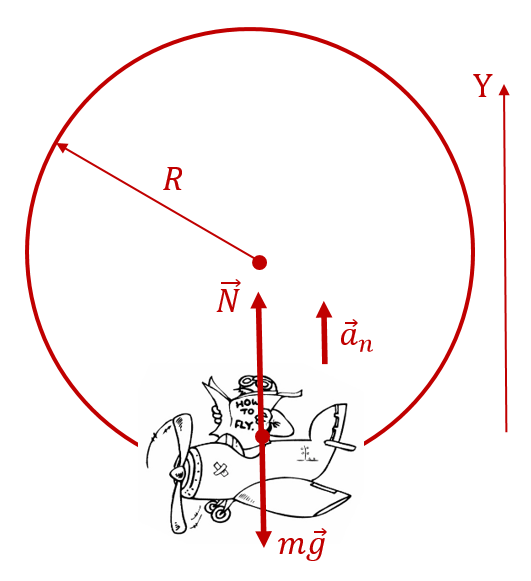
| Пример 3. Рассчитайте перегрузку, которую испытывает пилот самолёта, выполняющего «мёртвую петлю» в нижней точке траектории. Скорость самолёта в этой точке составляет 360 км/ч. Радиус «мёртвой петли» составляет 200 м. |
В нижней точке «мёртвой петли» на пилота будут действовать две силы: вниз — сила , вверх, к центру «мёртвой петли», — сила (со стороны кресла, в котором сидит пилот):
Туда же будет направлено центростремительное ускорение пилота 
, где 
км/ч 
м/с — скорость самолёта, 
— радиус «мёртвой петли». Тогда вновь в соответствии со 2-м законом Ньютона в проекции на ось, направленную вертикально вверх, получаем следующее уравнение:
![\[ N-mg = ma_n = \frac{m\upsilon^2}{R}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-da2862b088975ab67d22919e568ab5b6_l3.png "Rendered by QuickLaTeX.com")
Тогда вес равен 
. Итак, расчёт перегрузки даёт следующий результат:
![\[ \frac{m\left(g+\frac{\upsilon^2}{R}\right)}{mg} = 1+\frac{\upsilon^2}{gR} = 1+\frac{100^2}{10\cdot 200} = 6. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-bd0d66979d42352b265faec5a2a13b2e_l3.png "Rendered by QuickLaTeX.com")
Весьма существенная перегрузка. Спасает жизнь пилота только то, что действует она не очень длительно.
Ну и напоследок, рассчитаем перегрузку, которую испытывает водитель автомобиля при разгоне.
| Пример 4. Рассчитайте перегрузку, которую испытывает водитель автомобиля, разгоняющегося с места до скорости 180 км/ч за 10 с. |
Итак, конечная скорость автомобиля равна 
км/ч 
м/с. Если автомобиль ускоряется до этой скорости из состояния покоя за 
c, то его ускорение равно 
м/с2.
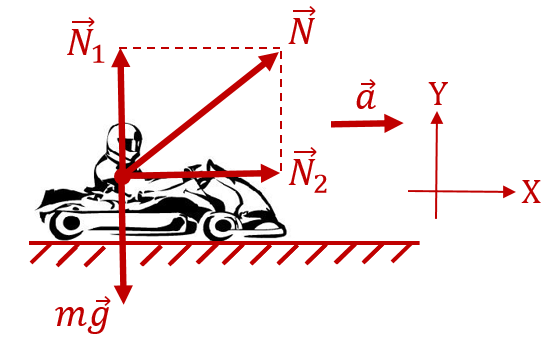
На водителя в процессе ускорения действуют две составляющие силы реакции опоры: со стороны седушки кресла (вертикальная составляющая) 
и со стороны спинки кресла (горизонатльная составляющая) 
:
Автомобиль движется горизонтально, следовательно, вертикальная составляющая силы реакции опоры уравновешена силой тяжести, то есть 
. В горизонтальном направлении водитель ускоряется вместе с автомобилем. Следовательно, по 2-закону Ньютона в проекции на ось, сонаправленную с ускорением, горизонтальная составляющая силы реакции опоры равна 
.
Величину общей силы реакции опоры найдём по теореме Пифагора: 
. Она будет равна модулю веса. То есть искомая перегрузка будет равна:
![\[ \frac{P}{mg} = \frac{N}{mg} = \frac{m\sqrt{g^2+a^2}}{mg} = \sqrt{1+\frac{a^2}{g^2}} \approx 1.12. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-57f6de2348b1dde4ac2ab7c3c900e407_l3.png "Rendered by QuickLaTeX.com")
Сегодня мы научились рассчитывать перегрузку. Запомните этот материал, он может пригодиться при решении заданий из ЕГЭ или ОГЭ по физике, а также на различных вступительных экзаменах и олимпиадах.
Материал подготовил репетитор по физике в Москве, Сергей Валерьевич
Смотрите также:
а можно реальный пример?
кирпич массой 3кг падает с высоты 2 метра на землю. Какова перегрузка при падении кирпича?
Так как кирпич находится в состоянии свободного падения, то его вес равен 0, как и перегрузка.
имелось ввиду — перегрузка в момент удара об землю
так это второй пример только сила реакции опоры направлена в низ . в момент удара ты знаешь скорость , можешь посчитать импульс и силу удара .
зная силу можно найти ускорение (а) которое будет (-а) ну а дальше все просто…
В этом случае можно рассчитать перегрузку?
Было написано: «Какова перегрузка при падении кирпича?» Процесс падения кирпича — это не то же самое, что момент удара о землю. Для того, чтобы найти перегрузку при ударе, нужно знать время этого удара.
дан был вес и высота, зная ускорение свободного падения — можно вычислить через сколько по времени кирпич достигнет земли. Силой трения о воздух — можно пренебречь.
Подразумевается, что кирпич — не отскакивает от земли (а если уж быть точным — то, это вы мне скажите — рассчитайте силу удара и сравните с силой притяжения, а также — постройте график изменения перегрузки при касании с поверхностью и…возможном отскоке) )))
Чтобы рассчитать перегрузку в момент удара о землю, нужно знать ускорение в момент этого удара. Его можно найти, если знать время удара, а не время, которое потребуется, чтобы кирпич достиг земли. Есть знать время удара, то тормозящая сила легко находится из 2го закона Ньютона. Потом эту силу нужно разделить на силу тяжести. Это и будет перегрузка.
Сергей хотел сказать время с момента касания поверхности до момента наступления покоя. время затраченное на то чтоб погасить энергию удара .
Формулы формулами, но для начинающих стоило бы написать на русском. Разгон на 10 кмч в секунду = стокото G
Строго говоря, зависит от того, в каком направлении разгоняетесь. Если на ракете вверх — одно значение, если на автомобиле вбок — другое. Оба случая, кстати, рассмотрены в статье.
данных в задаче не достаточно. Необходимо знать время соприкосновения с землей и время полной остановки. Ускорение ( т.е. замедление ) и даст вам перегрузку.
Человек падает с высоты 1,8 метра на Землю. Какую перегрузку испытает человек в момент столкновения ???
Чтобы решить такую задачу, нужно идти на ряд предположений. Например, что человек падает на ноги, приседает и в конце приседания полностью останавливается. При этом, предположим, в процессе приседания его голова и туловище прошли расстояние S = 1 м. Тогда скорость, с которой он будет падать непосредственно перед ударом подошвами ног о землю, равна v = корень(2*ускорение свободного падения*высоту) = корень(2*9.8*1.8) = 6 м/c. Тогда ускорение его тела в момент торможения составит усреднённо a = v^2/(2S) = 36/(2*1) = 18 м/с^2, что составляет перегрузку приблизительно 1.8G. Но это всё, как говорится, «прикидка к носу». Такие задачи так не решаются. По-хорошему, у них только одно решение — эмпирическое.
откуда в формуле про пилота взялась 1?
1 возникает после почленного деления числителя на знаменатель.
Сергей, спасибо за урок.
Разрабатываю подвесной аккумуляторный бокс для грузового автомобиля.
Ваши разъяснения — как нельзя кстати.
Ракета имеет стартовую массу 300 т. При старте запускаются 4 двигателя 1ой ступени, сила тяги каждого из которых 1000 кН, и 1 двигатель 2ой ступени, сила тяги 940 кН. Какую перегрузку испытывает космонавт в начале старта?
4*4000/10+940/10=494т — это тяга
494/300=1,65G — это перегрузка при старте
Мария, очевидно, что перегрузки не будет, она равна единице. В t0 (начало старта) сила тяги (сила реакции опоры) уравновешаны силой тяжести mg.
Нет, в момент, когда ракета начинает разгон, перегрузка, конечно, будет. Задача полностью аналогично разобранной в статье (пример 2).
У меня такой вопрос, допустим человек (75кг) падает с высоты 8.8 метра на куст высотой (2.3м) . Разница между ними 6.5 метра . Иресть он ускорялся 6.5 метра и тормозил 2.3метра . Какие перегрузки он испытывал при торможении ?
Есть похожий пример:
Падает груз массой 4кг, со скоростью 180 км/ч. Вопрос, какую нагрузку испытают стропы при открытии парашюта?)))
Какую перегрузку испытывали американские астронавты на второй космической скорости при входе в плотные слои атмосферы и до момента выпуска парашюта?
Сергей Валерьевич, в чем разница в сущности между силой тяжести, действующей на тело у поверхности земли и центробежной силой, которая действует на тело космонавта у поверхности корпуса космического корабля, если эти силы равны по величине? И можно ли сказать, что закон всемирного тяготения аналогичен закону центробежного ускорения?
Владимир, широкий вопрос, но, в принципе, хорошо представленный в литературе. Могу порекомендовать почитать про мысленный эксперимент «лифт Эйнштейна». И вообще всё, что касается принципа эквивалентности сил гравитации и инерции.
Летательный аппарат , летит со скоростью 14 махов ( около 17000 км/час .) и снижает скорость , для выполнения манёвра на скорости 400 метров/с . Какое время нужно затратить , на снижение скорости , чтобы пилот , не подвергался большим перегрузкам и оставался в сознании ( хотя бы не более 5g ) ? Есть какая-либо формула ?
Очинь памагло!!!!111
Огромное вам еловеческое спосибааааа!!!
Спасибо за статью. Очень помогла) Есть вопрос. Для проверки датчиков перегрузок необходимо собрать установку. Смогу ли я используя пример с мертвой петлей, прикрепить датчик к, предположим штанге, и вращая им в плоскости горизонта с определенной скоростью, меняя длинну штанги ( или напротив, меняя скорость при постоянном радиусе) добиться измерения показаний до 11g? Формулы останутся неизменными, я так понимаю.
Рад, что статья оказалась полезной. Да, верно, формулы останутся такими же, если предполагается вращение в вертикальной плоскости. Можно даже прикинуть, с какой скоростью придётся вращать штангу при заданной длине.
Решите задачу, пожалуйста!
Хомяк крутиться в стиралке при отжиме на 1200 оборотах в минуту. Диаметр барабана 0.5метра
Какую перегрузку испытвает хомяк?
13,8. См. пример 3
А как расчитать перегрузку, которую испытывает прыгун в воду в момент погружения в воду?
Определить перегрузки на вираже при крене γ=60°
Помогите пожалуйста
Задача: самолёт совершает горизонтальный полёт в неспокойном воздухе. Скорость горизонтальных порывов ветра 20м/с.скорость полёта 300 км/ч. Определить перегрузки самолёта.
не могу найти расчет перегрузки на тарзанке, сам получили силовой вариант решения, но он дает странные результаты, подскажите автора, у кого почитать…