Задача на относительность движения

Автор

Воскресенье, 14 августа, 2016

В данной статье репетитор по математике и физике рассказывает о простом способе решения достаточно сложной задачи на относительность движения, которому вас не научат в школе. Материал разобран на примере задачи о движущихся подводных лодках. Дочитайте эту статью до конца. Знания, которые вы получите, могут очень пригодиться на экзамене или олимпиаде по физике.

Подводная лодка-разведчик и подводная лодка-обнаружитель движутся на одной глубине по взаимно перпендикулярным траекториям. Лодка-разведчик — с запада на восток со скоростью \upsilon_1 = 45 км/ч, лодка-обнаружитель — с юга на север со скоростью \upsilon_2 = 28 км/ч. Известно, что в 12:00 лодка-разведчик находилась прямо по курсу относительно лодки-обнаружителя, и расстояние между ними составляло s = 106 км. Обнаружит ли в процессе движения лодка-обнаружитель присутствие лодки-разведчика, радиус обнаружения которой при текущих погодных условиях составляет r=90 км? Если да, то в какой момент времени это произойдёт?

Решение задачи на относительность движения

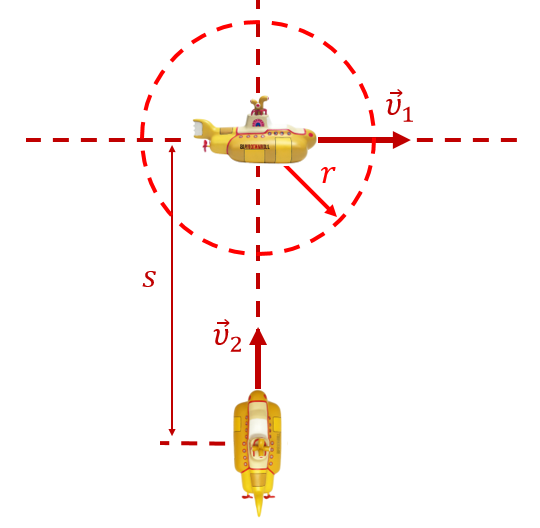
Для наглядности изобразим рисунок к задаче. Зона обнаружения лодки-разведчика обведём на рисунке красной пунктирной окружностью:

Рисунок к задаче про подводные лодки (на относительность движения)

Постараемся определить сперва минимальное расстояние, которое будет между подводными лодками в процессе их движения. Если решать задачу в  системе отсчёта, связанной с землёй, то для нахождения минимального расстояния между подводными лодками потребуется очень много времени и сил. Нужно будет найти зависимость расстояния между субмаринами от времени и исследовать получившуюся функцию на минимум с помощью производной. Всё это долго и сложно.

Разберём гораздо более простой способ. Для решения этой задачи используем принцип относительности движения. В чём он заключается? В том, что характер движения любого тела зависит от выбора системы отсчёта, относительно которой это движение рассматривается. Говорят, что Эйнштейн в своё время любил задавать вопрос: «В каком часу станция отходит от поезда?» Потому что с точки зрения кинематики для описания движения мы можем взять любую систему отсчёта, важно лишь правильно записать в ней кинематическое уравнение движения.

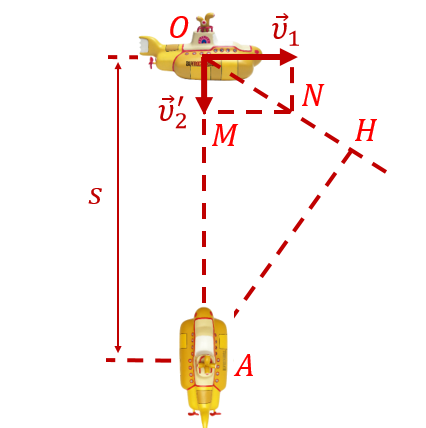
Вот и в этой задаче, гораздо проще связать систему отсчёта с положением лодки-обнаружителя. Тогда в этой системе отсчёта лодка-обнаружитель будет покоится, а лодка-разведчик станет двигаться вдоль по прямой ON, изображённой на рисунке:

Траектория движения одной подводной лодки в системе отсчёта, связанной с другой лодкой

Эта прямая задаётся вектором скорости движения лодки-разведчика в системе отсчёта, связанной с лодкой-обнаружителем. Этот вектор получен вычитанием вектора скорости лодки-обнаружителя относительно земли из вектора скорости лодки-разведчика относительно земли, в полном соответствии с принципом относительности движения.

Теперь, если посмотреть внимательно на получившийся рисунок, станет понятно, что искомое минимальное расстояние между лодками в процессе их движения будет равно длине перпендикуляра, проведённого из точки, в которой находится лодка-обнаружитель (точки A), к прямой, изображающей траекторию движения лодки-разведчика в системе отсчёта, связанной с лодкой-обнаружителем. То есть длине перпендикуляра AH. Осталось найти длину этого перпендикуляра, и задача будет решена. Довольно просто, не правда ли?

Видно, что треугольник OMN подобен треугольнику AOH (они оба прямоугольные, и у них есть общий угол O). Тогда спарведливо соотношение \frac{ON}{OA} = \frac{MN}{AH}. По теореме Пифагора находим численное значение длины ON, оно равно \sqrt{\upsilon_1^2+\upsilon_2^2}. Численные значения длин отрезков OA и MN равны s и \upsilon_1, соответственно. Тогда получаем, что

    \[ AH = s_{min} = \frac{s\upsilon_1}{\sqrt{\upsilon_1^2+\upsilon_2^2}}. \]

Расчёты дают результат s_{min} = 90 км.

Итак, минимальное расстояние между подводными лодками в процессе их движения в точности равно радиусу обнаружения лодки-разведчика, поэтому она будет обнаружена. Но в какой момент это произойдет?

Через столько времени с 12:00, сколько потребуется лодке-разведчику, чтобы в системе отсчёта, связанной с лодкой-обнаружителем, двигаясь со скоростью u = \sqrt{\upsilon_1^2+\upsilon_2^2} = 53 м/с, дойти до точки H. То есть пройти расстояние OH. Длину OH ищем по теореме Пифагора из прямоугольного треугольника OAH: OH = \sqrt{OA^2-AH^2} = \sqrt{s^2-s_{min}^2} = 56 км. Тогда искомое время равно \Delta t = \frac{OH}{u}. Расчёты дают следующий результат: \Delta t = 1.057 ч \approx 1 ч. 3 мин. 24 c. То есть момент обнаружения наступит примерно в 13:03:24.

Вот такое простое решение достаточно сложной задачи на относительность движения. Советую вам запомнить его и использовать при решении подобных задач на различных экзаменах и олимпиадах по физике.

Материал подготовлен репетитором по физике в Москве, Сергеем Валерьевичем

Смотрите также:

Метки: , , ,
Опубликовано в категории Методическая копилка | 4 комментария »

Комментарии

  1. Дмитрий:
    15.08.2016 в 09:38

    Судя по решению, имелось ввиду, что лодки находятся на одной глубине. Но в условии об этом ничего не сказано.

    Ответить
    1. Сергей:
      15.08.2016 в 17:12

      Написано, что в 12:00 лодка-разведчик была прямо по курсу относительно лодки-обнаружителя. По смыслу она не могла погружаться, когда это случилось, поэтому они могли быть только на одной глубине.

      Ответить
  2. Дмитрий:
    02.07.2018 в 16:03

    А почему бы сразу не применить т. Пифагора, затем просто решить квадратное уравнение?
    (106-28*t)^2+(45*t)^2=90^2
    2809*t^2-5936*t+3136=0
    D=0
    t=5936/5618=1,0566…

    Ответить
    1. Сергей:
      03.07.2018 в 15:55

      Можно и так, конечно. Только вот квадратное уравнение получается, как из ночного кошмара 🙂

      Ответить

Добавить комментарий