Репетитору по математике часто приходится сталкиваться с отсутствием у старшеклассников навыков решения простейших уравнений и неравенств с модулем. Между тем среди заданий С3 или С5 из ЕГЭ по математике таковые могут встретиться. Даже если их не будет на экзамене в явном виде, в процессе выполнения некоторых задач из ЕГЭ вам, возможно, придется столкнуться с решением того или иного задания с модулем. Поэтому научиться решать уравнения и неравенства с модулем должен каждый выпускник средней школы. В данной статье рассмотрены некоторые способы их решения. Присутствует также видеоразбор решения одного уравнения, содержащего модуль.
Считается, что чем больше способов решения существует у задачи, тем она интереснее с математической точки зрения. Уравнения и неравенства с модулями можно поэтому смело назвать интересными. Рассмотрим пример.
![]()
Решение. Постараемся найти как можно большее количество решений данного уравнения. Подробное объяснение решений смотрите в видеоуроке.
Способ №1. Решение возведением в квадрат. Просто возводим обе части уравнения в квадрат. При этом не забываем, что подобное преобразование не является равносильным. Из-за этого могут появиться посторонние корни, поэтому полученные решения необходимо будет проверить прямой подстановкой в исходное уравнение.
![]()
![]()
![]()
Путем прямой подстановки полученных решений в исходное уравнение убеждаемся, что посторонних корней среди них нет. На самом деле в данном конкретном задании отсутствует необходимость проверки корней. Возведение обеих частей этого уравнения в квадрат не может привести к приобретению посторонних решений. Подумайте самостоятельно, почему это так.
Способ №2. Метод интервалов. Не совсем верное название, но мы его здесь употребим, поскольку в методической литературе оно встречается. Для решения нам потребуется найти значение переменной ![]() при котором подмодульное выражение обращается в ноль:
при котором подмодульное выражение обращается в ноль: ![]()
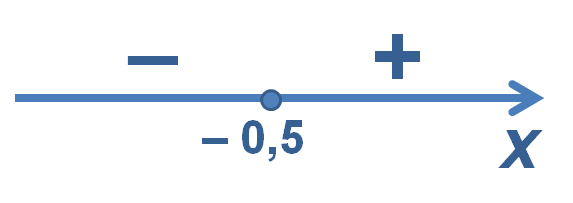
![]() Наносим эту точку на числовую прямую и определяем знаки подмодульного выражения на полученных промежутках.
Наносим эту точку на числовую прямую и определяем знаки подмодульного выражения на полученных промежутках.
Далее на каждом промежутке раскрываем знак модуля в соответствии с полученными данными:
- при
![Rendered by QuickLaTeX.com x\in\left(-\mathcal{1};-\frac{1}{2}\right]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f00f1b35dce8de4b90489e44f590c4a3_l3.png) подмодульное выражение отрицательно, и модуль раскрывается со знаком минус:
подмодульное выражение отрицательно, и модуль раскрывается со знаком минус: 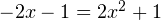 или
или 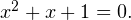 Дискриминант этого квадратного уравнения отрицателен, корней нет.
Дискриминант этого квадратного уравнения отрицателен, корней нет. - при
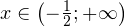 подмодульное выражение положительно, и модуль раскрывается со знаком плюс:
подмодульное выражение положительно, и модуль раскрывается со знаком плюс: 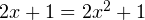 или
или 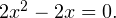 Корни уравнения
Корни уравнения 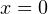 и
и 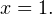 Оба принадлежат рассматриваемому нами промежутку.
Оба принадлежат рассматриваемому нами промежутку.
Способ №3. Замена уравнения смешанной системой. Известно, что:
![Rendered by QuickLaTeX.com \[ |f(x)| = g(x)\Leftrightarrow \begin{cases} g(x)\geqslant 0 \\ \left[\begin{array}{l}f(x) = g(x) \\ f(x)=-g(x)\end{array}\right. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-34af13aef4473e853fa9a650beb987a8_l3.png)
Для тех, кто не знает, какой именно смысл вкладывается в математике в фигурные и квадратные скобки, рекомендую ознакомиться со статьей «Решение систем логарифмических и показательных неравенств». То есть в нашем случае:
![Rendered by QuickLaTeX.com \[ \begin{cases} 2x^2+2\geqslant 0, \\ \left[\begin{array}{l}2x+1 = 2x^2+1, \\ 2x+1 =-2x^2-1.\end{array}\right. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ecdeac771274b7950ba047bdab2bd277_l3.png)
Легко заметить, что первое неравенство выполняется при любом значении ![]() Следовательно, в составе системы на него вообще можно не обращать внимания. Ситуация несколько упрощается:
Следовательно, в составе системы на него вообще можно не обращать внимания. Ситуация несколько упрощается:
![]()
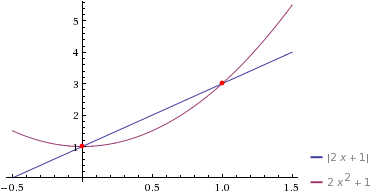
Способ №4. Графический. Строим в одной системе координат графики функции ![]() и
и ![]() Абсциссы точек их пересечения будут являться решениями уравнения. Метод менее точный, но более наглядный. Видно, что это все те же
Абсциссы точек их пересечения будут являться решениями уравнения. Метод менее точный, но более наглядный. Видно, что это все те же ![]() и
и ![]()
На этом список стандартных способов решения данного уравнения с модулем исчерпан. Придумайте свои нестандартные.
Простейшие уравнения с модулем
|
|
![]()
Решение. Перепишем уравнение в виде:
![]()
Получается, что модуль выражения равен этому выражению, взятому с противоположным знаком. Такое возможно только в том случае, если данное выражение отрицательно или равно нулю:
![]()
Ответ: ![]()
Задача для самостоятельного решения №1. Решите уравнение
![]()
Показать ответ
|
|
![]()
Решение. Исходное уравнение равносильно системе:
![Rendered by QuickLaTeX.com \[ \begin{cases} \sin x\geqslant 0, \\ \left[\begin{array}{l} \cos x = \sin x, \\ \cos x = -\sin x \end{array}\right.\end{cases}\Leftrightarrow \begin{cases} 2\pi k\leqslant x\leqslant \pi+2\pi k, \\ \left[\begin{array}{l}x = \frac{\pi}{4}+2\pi n, \\ x = -\frac{\pi}{4}+2\pi z.\end{array}\right.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ea16cf1fbbbe1303d172b4ce504a4af8_l3.png)
Обе части последних двух уравнений разделили на ![]() В данном случае
В данном случае ![]() В противном случае
В противном случае ![]() а это невозможно, поскольку
а это невозможно, поскольку ![]()
Окончательно, получаем: ![]()
Ответ: ![]()
Задача для самостоятельного решения №2. Решите уравнение:
![]()
Примечание. Для решения этого задания потребуется знание формулы суммы и разности синусов.
Показать ответ
![]()
![]()
|
|
![Rendered by QuickLaTeX.com \[ \left|\frac{x^2}{x-1}-x\right|+\left|\frac{x}{x-1}-2\right|= \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8a821c678aaba8aee758723a50a988ba_l3.png)
![]()
Решение. Перепишем уравнение в виде:
![Rendered by QuickLaTeX.com \[ \left|\frac{x^2}{x-1}-x\right|+\left|\frac{x}{x-1}-2\right|= \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8a821c678aaba8aee758723a50a988ba_l3.png)
![]()
Сумма модулей равна сумме подмодульных выражений. Это возможно только в том случае, когда оба подмодульных выражения неотрицательны:
![Rendered by QuickLaTeX.com \[ \begin{cases}\frac{x^2}{x-1}-x\geqslant 0, \\ \frac{x}{x-1}-2\geqslant 0.\end{cases}\Leftrightarrow \begin{cases}\frac{x}{x-1}\geqslant 0, \\ \frac{2-x}{x-1}\geqslant 0.\end{cases}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-872735d1234345fca2af019c3f6302af_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}x\in(-\mathcal{1};0]\cup(1;+\mathcal{1}), \\ x\in(1;2]\end{cases}\Leftrightarrow x\in(1;2]. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-70d727b86dcd1695c0f86c0849498fa6_l3.png)
Ответ: ![]()
Задача для самостоятельного решения №3. Решите уравнение:
![]()
Показать ответ
|
|
![]()
Решение. Сумма модулей равна модулю суммы подмодульных выражений. Это возможно только в том случае, когда оба подмодульных выражения одновременно либо неотрицательны, либо неположительны. То есть:
![]()
![]()
![]()
Ответ: ![]()
Задача для самостоятельного решения №4. Решите уравнение:
![Rendered by QuickLaTeX.com \[ \left|\frac{x+2}{x+1}+4\right|+\left|\frac{3-x}{x+1}-3x-3\right|=\left|1-3x+\frac{5}{x+1}\right|. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-9002d44afe91f55060d21e1a8e4831a2_l3.png)
Показать ответ
Простейшие неравенства с модулем
|
|
![]()
Решение. Исходное неравенство равносильно следующей системе неравенств:
![Rendered by QuickLaTeX.com \[ \begin{cases}x+1\leqslant 2x, \\ x+1\geqslant -2x \end{cases}\Leftrightarrow \begin{cases}x\geqslant 1, \\ x\geqslant -\frac{1}{3}.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c71d9c36dadd2498c31976b1db8d3db9_l3.png)
Ответ: ![]()
Задача для самостоятельного решения №5. Решите неравенство:
![]()
Показать ответ
|
|
![]()
Решение. Исходное неравенство равносильно следующей совокупности неравенств:
![]()
Ответ: ![]()
Задача для самостоятельного решения №6. Решите неравенство:
![]()
Показать ответ
|
|
![]()
Решение. Исходное неравенство равносильно следующему неравенству:
![]()
Ответ: ![]()
Задача для самостоятельного решения №8. Решите неравенство:
![Rendered by QuickLaTeX.com \[ \left|8x^2+\frac{1}{x}\right|\leqslant 8x^2+\frac{1}{x}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ac7b08268c611ea8a1bcfab973fa4e0a_l3.png)
Показать ответ
|
|
![]()
Решение. Исходное неравенство равносильно следующему неравенству:
![]()
Ответ: ![]()
Задача для самостоятельного решения №9. Решите неравенство:
![Rendered by QuickLaTeX.com \[ \left|\frac{1-x}{1+3x}\right|>|1+x|. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-17e795123303a44561d831a6b9560a5d_l3.png)
Показать ответ
Сергей Валерьевич
Частный преподаватель по математике


![Rendered by QuickLaTeX.com \[|f(x)| = g(x)\Leftrightarrow \begin{cases} g(x)\geqslant 0 \\ \left[\begin{array}{l}f(x) = g(x) \\ f(x)=-g(x)\end{array}\right. \end{cases}\]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-740a39d0ac99ef5d8e68882144e24026_l3.png)
![Rendered by QuickLaTeX.com \[|f(x)|+|g(x)| = f(x) + g(x)\Leftrightarrow \begin{cases} f(x)\geqslant 0 \\ g(x)\geqslant 0 \end{cases}\]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-994b4985d3419941de51c48ab376cb44_l3.png)
![Rendered by QuickLaTeX.com \[|f(x)|+|g(x)| = f(x) - g(x)\Leftrightarrow \begin{cases} f(x)\geqslant 0\\g(x)\leqslant 0 \end{cases}\]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-42e1e1de50728d7438f88640f80f7cd9_l3.png)
![Rendered by QuickLaTeX.com \[|f(x)|\leqslant g(x)\Leftrightarrow \begin{cases}f(x)\leqslant g(x) \\ f(x)\geqslant -g(x)\end{cases}\]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-95700a1d8bd72a78b0077fce72a17738_l3.png)
Спасибо большое! Очень пригодилось!
Спасибо большое! Готовлюсь к годовой по алгебре, все позабывал, не мог найти метод интервалов. У вас нашел, спасибо еще раз!
Здравствуйте. Мне очень понравился урок, вспомнила некоторые довольно удобные методы решения уравнений с модулями. Но хочу отметить, в третьем задании для самостоятельного решения допущена опечатка, там пропущен квадрат во втором модуле, из-за чего не получалось решить уравнение. Спасибо).
Здравствуйте. Да, действительно, квадрат у икса потерялся. Уже исправил. Большое спасибо.
извините, но разве в задаче для самостоятельного решения №1 ответ не 3?
Определенно, нет.
Большое спасибо. С большим удовольствием повторила и объяснила внукам. Люблю математику.
Очень рад, что этот материал оказался Вам полезен!
Простите, но теория перед 6-м примером не подтверждается решением…Сами посмотрите. простая проверка-в ответ не входит число 2\3. а простая подстановка дает верное неравенство. Стала решать Вашим способом неравенcтва из профильного учебника Мордковича для 10кл, а ничего не сходится с ответом..(5.17)..Пересмотрите, пожалуйста..Так же нельзя…
Если подставить 2/3, то слева в неравенстве получится |2*2/3-1| = |4/3-1| = |1/3| = 1/3, а это никак не больше и не равно 2/3.
Спасибо за ваш материал! А что теперь делать после этих заданий? Что еще порешать?
Спасибо огромное, очень полезный материал!!!!
Уравнения и неравенства
Великолепно. Я нашёл то, что искал. Спасибо
спасибо, очень помогло. жаль, что этот материал проходится в школе только поверхностно