 Решение задач с параметрами требует наличия определенной математической культуры. С реше-нием задач с параметрами приходится сталкиваться не только в математике. Очень многие законы и закономерности из физики, эконо-мики и других областей описываются уравнениями и неравенствами с параметрами. Фактически, решая задачи по физике, химии, экономике и некоторым другим школьным дисциплинам, ученик имеет дело с параметрами. Решению задач с параметрами посвящено большое количество учебно-методической литературы. В данной статей приводятся лишь некоторые представления о том, как рассуждают при решении подобных заданий. С этой целью рассмотрены несколько примеров, большая часть которых взята из вариантов ЕГЭ по математике прошлых лет (задача C5).
Решение задач с параметрами требует наличия определенной математической культуры. С реше-нием задач с параметрами приходится сталкиваться не только в математике. Очень многие законы и закономерности из физики, эконо-мики и других областей описываются уравнениями и неравенствами с параметрами. Фактически, решая задачи по физике, химии, экономике и некоторым другим школьным дисциплинам, ученик имеет дело с параметрами. Решению задач с параметрами посвящено большое количество учебно-методической литературы. В данной статей приводятся лишь некоторые представления о том, как рассуждают при решении подобных заданий. С этой целью рассмотрены несколько примеров, большая часть которых взята из вариантов ЕГЭ по математике прошлых лет (задача C5).
Решение «типичных» задач с параметрами
Решение.
1) Начнем с рассмотрения случая, когда ![]() . Тогда уравнение принимает вид
. Тогда уравнение принимает вид ![]() , откуда получаем, что
, откуда получаем, что ![]() — положительный корень. Значит данное значение
— положительный корень. Значит данное значение ![]() нам подходит. Запомнили.
нам подходит. Запомнили.
2) Теперь рассматриваем случай, когда ![]() . Разделим обе части уравнения на
. Разделим обе части уравнения на ![]() . В результате получаем следующее квадратное уравнение:
. В результате получаем следующее квадратное уравнение:
![]()
Так как ветви соответствующей параболы направлены вверх, данное уравнение имеет два положительных корня в том случае, если эта парабола пересекает ось OY в точке, находящейся выше нуля (то есть значение соответствующей квадратичной функции при ![]() положительно), абсцисса вершины параболы положительна, а дискриминант квадратного уравнения неотрицателен. То есть имеет место следующая система:
положительно), абсцисса вершины параболы положительна, а дискриминант квадратного уравнения неотрицателен. То есть имеет место следующая система:
![Rendered by QuickLaTeX.com \[ \begin{cases} \frac{a+3}{a-2}>0 \\ \frac{a}{a-2}>0 \\ \frac{6-a}{(a-2)^2}\geqslant 0. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-6934153cefc4872fe1d3b7a0276d59a9_l3.png)
Решая данную систему неравенств, получаем промежуточный ответ: ![]() .
.
3) Объединяем решения, полученные в предыдущих двух пунктах. В результате получаем окончательный ответ: ![]() .
.
Задача для самостоятельного решения №1. Для каждого значения ![]() решите уравнение
решите уравнение ![]()
1) при ![]() уравнение будет иметь один корень
уравнение будет иметь один корень ![]()
2) при ![]() будет два корня
будет два корня ![]()
![]()
3) при ![]() будет три корня
будет три корня
![]()
![]()
![]()
4) при ![]() будет два корня
будет два корня ![]()
![]()
5) при ![]() будет один корень
будет один корень ![]()
Решение.
Используем следующую замену: ![]() . Тогда первоначальное уравнение принимает вид:
. Тогда первоначальное уравнение принимает вид: ![]() Полученное уравнение с параметром можно исследовать с помощью метода, использованного нами при решении предыдущего задания. Однако для разнообразия предлагаю воспользоваться здесь альтернативным подходом.
Полученное уравнение с параметром можно исследовать с помощью метода, использованного нами при решении предыдущего задания. Однако для разнообразия предлагаю воспользоваться здесь альтернативным подходом.
Исходное уравнение будет иметь единственный корень в том случае, если у данного уравнения будет один положительный корень либо два корня, один из которых положительный, другой — отрицательный или равный нулю.
1) Дискриминант уравнения равен: ![]() . Один корень это уравнение будет иметь в том случае, если полученный дискриминант окажется равным нулю, то есть при
. Один корень это уравнение будет иметь в том случае, если полученный дискриминант окажется равным нулю, то есть при ![]() . При этом корень
. При этом корень ![]() — положителен. Данное значение
— положителен. Данное значение ![]() нам подходит. Запомнили.
нам подходит. Запомнили.
2) Рассматриваем случай, когда существует два корня, один из которых положителен, другой — неположителен. Условия, при которых эта ситуация реализуется, могут быть записаны следующим образом:
![Rendered by QuickLaTeX.com \[ \begin{cases} a<\frac{13}{4}, \\ \frac{3+\sqrt{13-4a}}{2}>0,\\ \frac{3-\sqrt{13-4a}}{2}\leqslant 0 \end{cases}\Leftrightarrow a\in(-\mathcal{1};1]. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-98af4f25194bca783bb29d3e4d38fbf4_l3.png)
Окончательно: ![]() .
.
Задача для самостоятельного решения №2. Найдите все значения ![]() при которых уравнение
при которых уравнение ![]() имеет единственное решение.
имеет единственное решение.
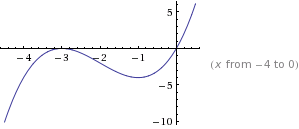
Решение. Перепишем уравнение в виде: ![]() . Найдем промежутки возрастания и убывания функции
. Найдем промежутки возрастания и убывания функции ![]() . Для этого найдем сперва ее производную:
. Для этого найдем сперва ее производную:
![]()
Нули производной равны ![]()
Производная принимает положительные значения на промежутке ![]() , на промежутке
, на промежутке ![]() она принимает отрицательные значения. То есть в точке
она принимает отрицательные значения. То есть в точке ![]() возрастание функции сменяется ее убыванием, то есть это точка максимума. Значение функции в этой точке:
возрастание функции сменяется ее убыванием, то есть это точка максимума. Значение функции в этой точке: ![]() . Напротив, в точке
. Напротив, в точке ![]() убывание функции сменяется ее возрастанием, то есть это точка минимума. Значение функции в этой точке:
убывание функции сменяется ее возрастанием, то есть это точка минимума. Значение функции в этой точке: ![]() .
.
Следовательно, три решения исходное уравнение будет иметь в том случае, если прямая ![]() на координатной плоскости будет располагаться выше прямой
на координатной плоскости будет располагаться выше прямой ![]() и ниже прямой
и ниже прямой ![]() . Значит верно двойное неравенство:
. Значит верно двойное неравенство: ![]() . Откуда получаем окончательный ответ:
. Откуда получаем окончательный ответ: ![]() .
.
Задача для самостоятельного решения №3. Найдите все значения параметра ![]() при которых уравнение
при которых уравнение ![]()
![]() не имеет решений.
не имеет решений.
Не сходится с ответом?
Показать подсказкуРешение задач с параметрами повышенной сложности
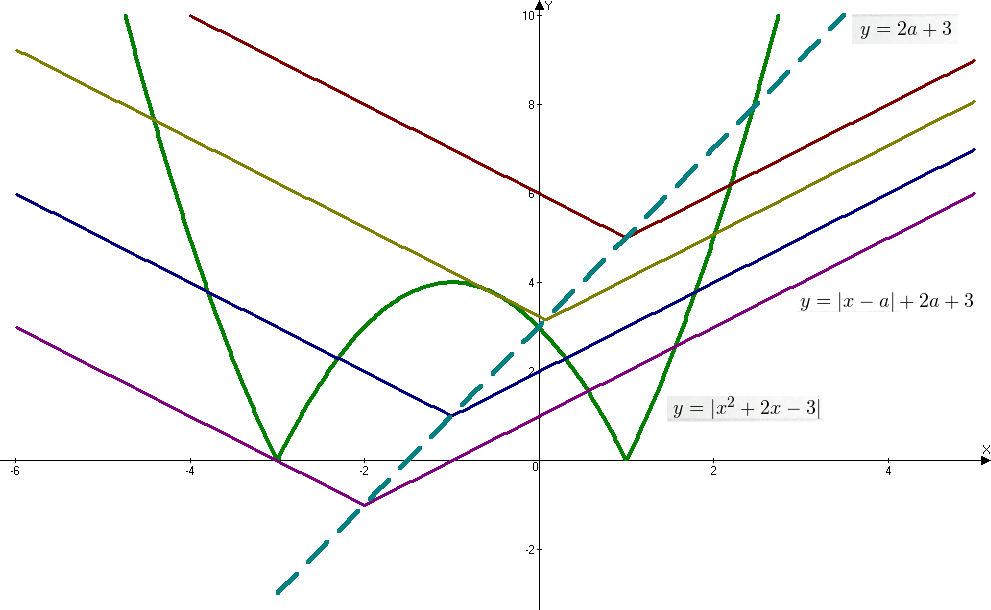
Решение. Используем графический метод решения. График функции ![]() отличается от параболы
отличается от параболы ![]() только тем, что отрицательная ее область зеркально отражается вверх относительно оси OX (ведь модуль не может принимать отрицательных значений).
только тем, что отрицательная ее область зеркально отражается вверх относительно оси OX (ведь модуль не может принимать отрицательных значений).
График функции ![]() представляет собой всем известную «галочку», вершина которой смещена в точку
представляет собой всем известную «галочку», вершина которой смещена в точку ![]() . В зависимости от значений параметра
. В зависимости от значений параметра ![]() возможны следующие варианты взаимного расположения этих графиков на координатной плоскости:
возможны следующие варианты взаимного расположения этих графиков на координатной плоскости:
Видно, что три решения уравнение будет в случае фиолетовой и бежевой «галочки». Первый случай выполняется при условии выполнения равенства ![]()
![]() Во втором случае оба модуля раскрываются со отрицательным знаком. В результате приходим к уравнению
Во втором случае оба модуля раскрываются со отрицательным знаком. В результате приходим к уравнению ![]() . Его дискриминант должен быть равен нулю, чтобы получилось одно пересечение (касание). То есть оказывается, что
. Его дискриминант должен быть равен нулю, чтобы получилось одно пересечение (касание). То есть оказывается, что ![]()
Ответ: ![]()
Задача для самостоятельного решения №4. При каких ![]() уравнение
уравнение ![]() имеет ровно три корня?
имеет ровно три корня?
![Rendered by QuickLaTeX.com \[ \begin{cases} x^2+y^2 = 2a, \\ 2xy=2a-1 \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-19bcb1b0bbf7da3b9b3b483c3601a6b1_l3.png)
имеет ровно два решения.
Решение. Вместо ![]() во втором уравнении подставляем
во втором уравнении подставляем ![]() из первого, тогда второе уравнение системы принимает вид:
из первого, тогда второе уравнение системы принимает вид:
![]()
![]()
Обращаем внимание на то, что каждому найденному значению ![]() будет соответствовать единственное значение
будет соответствовать единственное значение ![]() , такая пара
, такая пара ![]() будет одним решением системы. Подставляя полученные выражения во второе уравнение системы, получаем два квадратичных уравнения:
будет одним решением системы. Подставляя полученные выражения во второе уравнение системы, получаем два квадратичных уравнения: ![]() и
и ![]() . Дискриминант и того, и другого равен
. Дискриминант и того, и другого равен ![]() .
.
Нам нужно, чтобы у каждого из этих уравнений было по одному решению, тогда у исходной системы их будет два. Это условие выполняется в том случае, когда полученный дискриминант равен нулю. Итак, окончательный ответ: ![]() .
.
Задача для самостоятельного решения №5. Найдите все значения параметра ![]() , при каждом из которых неравенство
, при каждом из которых неравенство ![]() выполнено для любых значений переменной
выполнено для любых значений переменной ![]() из отрезка
из отрезка ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{cases}\log_a y = (x^2-2x)^2, \\ x^2+y=2x\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-cf533a649e0f501157e2e7f6bef06260_l3.png)
имеет ровно два решения.
Решение. Преобразуем систему к следующему виду:
![Rendered by QuickLaTeX.com \[ \begin{cases} \log_a y = (2x-x^2)^2, \\ y = 2x-x^2. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-08384ad6d4c0cc861cd8be0a7fd58f01_l3.png)
Поскольку параметр ![]() находится в основании логарифма, на него накладываются следующие ограничения:
находится в основании логарифма, на него накладываются следующие ограничения: ![]() . Поскольку переменная
. Поскольку переменная ![]() стоит под знаком логарифма, на нее накладывается следующее ограничение:
стоит под знаком логарифма, на нее накладывается следующее ограничение: ![]() .
.
Скомбинировав оба уравнения системы, переходим к уравнению: ![]() . В зависимости от того, какие значения принимает параметр
. В зависимости от того, какие значения принимает параметр ![]() , возможны два случая:
, возможны два случая:
1) Пусть ![]() В этом случае функция
В этом случае функция ![]() убывает в области допустимых значений, а функция
убывает в области допустимых значений, а функция ![]() возрастает в той же области. Вспомнив внешний вид графиков соответствующих функций (кто не помним, может ознакомиться с этой статьей), осознаем, что корень у уравнения один, при этом он меньше 1. Второе уравнение системы и вся система в целом имеют, следовательно, два решения в силу того, что дискриминант уравнения
возрастает в той же области. Вспомнив внешний вид графиков соответствующих функций (кто не помним, может ознакомиться с этой статьей), осознаем, что корень у уравнения один, при этом он меньше 1. Второе уравнение системы и вся система в целом имеют, следовательно, два решения в силу того, что дискриминант уравнения ![]() при
при ![]() положителен. Рассматриваемый случай нам полностью подходит.
положителен. Рассматриваемый случай нам полностью подходит.
2) Пусть теперь ![]() . В этом случае функция
. В этом случае функция ![]() возрастает на области допустимых значений, и функция
возрастает на области допустимых значений, и функция ![]() возрастает в этой области. Вспомнив внешний вид графиков соответствующих функций, осознаем, что пересечься в одной точке они могут только в случае касания друг друга. Однако, касание это может произойти лишь в точке, абсцисса которой больше 1. Второе уравнение системы и вся система в целом, следовательно, иметь решений не будут в силу того, что дискриминант уравнения
возрастает в этой области. Вспомнив внешний вид графиков соответствующих функций, осознаем, что пересечься в одной точке они могут только в случае касания друг друга. Однако, касание это может произойти лишь в точке, абсцисса которой больше 1. Второе уравнение системы и вся система в целом, следовательно, иметь решений не будут в силу того, что дискриминант уравнения ![]() при
при ![]() отрицателен.
отрицателен.
Итак, окончательный ответ: ![]() .
.
Задача для самостоятельного решения №6. Для каждого допустимого значения ![]() решите неравенство
решите неравенство ![]()
![]() и найдите, при каких значениях
и найдите, при каких значениях ![]() множество решений неравенства представляет собой промежуток длины
множество решений неравенства представляет собой промежуток длины ![]()
1) при ![]() получаем
получаем ![]()
2) при ![]() получаем
получаем ![]()
Отрезок длины ![]() получается при
получается при ![]()
Решение. Перепишем уравнение в виде:
![]()
Рассмотрим функцию:
![]()
При ![]() первый модуль раскрывается со знаком плюс, и функция принимает вид:
первый модуль раскрывается со знаком плюс, и функция принимает вид: ![]() . Очевидно, что при любом раскрытии модулей в итоге будет получаться линейная функция с коэффициентом
. Очевидно, что при любом раскрытии модулей в итоге будет получаться линейная функция с коэффициентом ![]() , то есть эта функция на данном промежутке возрастает.
, то есть эта функция на данном промежутке возрастает.
Рассмотрим теперь промежуток, на котором ![]() . В этом случае первый модуль раскрывается с минусом и функция принимает следующий вид:
. В этом случае первый модуль раскрывается с минусом и функция принимает следующий вид: ![]() . Также легко видеть, что при любом раскрытии модулей в итоге будет получаться линейная функция с коэффициентом
. Также легко видеть, что при любом раскрытии модулей в итоге будет получаться линейная функция с коэффициентом ![]() , то есть на этом промежутке функция убывает.
, то есть на этом промежутке функция убывает.
Итак, мы получили, что ![]() — точка минимума данной функции. А это означает, что для того, чтобы график данной функции пересекал ось OX в двух точках (то есть у исходного уравнения уравнения было два решения), значение функции в точке минимума должно быть меньше нуля. То есть имеет место неравенство:
— точка минимума данной функции. А это означает, что для того, чтобы график данной функции пересекал ось OX в двух точках (то есть у исходного уравнения уравнения было два решения), значение функции в точке минимума должно быть меньше нуля. То есть имеет место неравенство: ![]() .
.
После несложных преобразований получаем окончательный ответ: ![]()
Задача для самостоятельного решения №7. При каких значениях ![]() уравнение
уравнение ![]() имеет ровно одно решение на промежутке
имеет ровно одно решение на промежутке ![]()
Не сходится с ответом?
Показать подсказкуВсе равно не получается?
Показать решение ![Rendered by QuickLaTeX.com \[ \begin{cases} a^{2x-y-1} = x+3y-7, \\ 4y-x = 6 \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-bcb8004114c8ecf2f82435ab63160cd4_l3.png)
имеет ровно два решения.
Решение.
Выразим ![]() из второго уравнения и подставим в первое, получаем:
из второго уравнения и подставим в первое, получаем:
![Rendered by QuickLaTeX.com \[ \begin{cases} a^{2x-y-1} = x+3y-7, \\ x=4y-6\end{cases}\Leftrightarrow \begin{cases} a^{7y-13} = 7y-13, \\ x=4y-6. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-a391071ab6052177cb952a521cfa1e32_l3.png)
Для того, чтобы данная система имела два решения, необходимо, чтобы два решения имело первое уравнение этой системы. Нас интересуют только ![]()
1) При ![]() получаем линейное уравнение:
получаем линейное уравнение: ![]() которое имеет одно решение. Этот случай не подходит.
которое имеет одно решение. Этот случай не подходит.
2) Рассматриваем случай, когда ![]() Уравнение принимает вид:
Уравнение принимает вид: ![]() . Его правая часть представляет из себя возрастающую функцию, левая — убывающую. Это означает, что если у такого уравнения есть решение, то оно единственное. Этот случай нам не подходит.
. Его правая часть представляет из себя возрастающую функцию, левая — убывающую. Это означает, что если у такого уравнения есть решение, то оно единственное. Этот случай нам не подходит.
3) Теперь рассмотрим случай, когда ![]() В зависимости от конкретного значения параметра
В зависимости от конкретного значения параметра ![]() уравнение вида
уравнение вида ![]() может не иметь решений (нет точек пересечения соответствующих графиков), иметь одно решение (прямая касается экспоненты), иметь два решения (две точки пересечения). Нам подходит последний случай.
может не иметь решений (нет точек пересечения соответствующих графиков), иметь одно решение (прямая касается экспоненты), иметь два решения (две точки пересечения). Нам подходит последний случай.
Разберемся со случаем, когда прямая касается экспоненты. Пусть ![]() — абсцисса точки касания. В этой точке производная к экспоненте равняется единице (тангенс угла наклона касательной), кроме того значения обоих функций совпадают, то есть имеет место система:
— абсцисса точки касания. В этой точке производная к экспоненте равняется единице (тангенс угла наклона касательной), кроме того значения обоих функций совпадают, то есть имеет место система:
![Rendered by QuickLaTeX.com \[ \begin{cases} a^{\tau}\ln a = 1, \\ a^{\tau} = \tau \end{cases}\Leftrightarrow \begin{cases} a^{\tau} = \frac{1}{\ln a}, \\ a^{\tau} = \tau \end{cases}\Leftrightarrow \tau = \frac{1}{\ln a}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-d8d685c10070cb1cf3f9917150102cc0_l3.png)
![]()
Если значение параметра окажется меньше, точек пересечения прямой и экспоненты уже будет две. Итак, окончательный ответ: ![]()
Задача для самостоятельного решения №8. Найти все значения ![]() при каждом из которых наименьшее значение функции
при каждом из которых наименьшее значение функции ![]() больше, чем
больше, чем ![]()
На сегодня на этом все. Следите за обновлениями, учите математику, задавайте свои вопросы в комментариях. Удачи вам! А напоследок случай из жизни Сократа о значимости некоторых параметров.
Репетитор по математике на Юго-Западной
Сергей Валерьевич
— Сколько часов пути до города?
Сократ ответил:
— Иди…
Путник пошел, и, когда он прошел двадцать шагов, Сократ крикнул:
— Два часа!
— Что же ты мне сразу не сказал? — возмутился тот.
— А откуда я знал, с какой скоростью ты будешь идти?!

Скажите, пожалуйста, почему в задании N1 в ответе указано, по сути пересечение, а не объединение решений, ведь разные корни квадратного уравнения это объединение? Или я не понимаю еще задач с параметрами?
Нет, указано именно объединение.
Или Вы имеете ввиду, почему во втором случае при a<>2 мы взяли систему. Тогда это, потому что оба корня должны быть положительны одновременно.
В примере №5 — ошибка.
Очепятка, исправил, спасибо.
Добрый день, почему в Примере 2
а<13/4
Потому что только при этих значениях дискриминант будет положительным, и корней будет 2.
Здравствуйте. Почему в Примере 8 тангенс угла наклона касательной равен 1?
Потому что уравнение имеет вид a^t=t, а прямая y=t — это биссектриса первой координатной четверти, у нее тангенс угла наклона равен 1.
Здравствуйте.Скажите, пожалуйста, почему в задании N1, не рассматривается случай при а=0?Если а=0, х=-+1.5^1/2 =>х=1.5^1/2 подходит под условие х>0
Здравствуйте. Ну там по условию имеется ввиду, что оба корня должны быть положительны.
Здравствуйте. Как в первом примере решили неравенства ?
Здравствуйте, о методах решения неравенств читайте в этой статье.
В примере 1 действии 2 в системе 1-ое уравнение у меня имеет отрицательный корень, т. е. a ^ 2 — a + 6 = 0
Какой именно отрицательный корень?
Во 2 примере не указано, что единственный корень должен быть положительным или отрицательным, т.е по сути мы же должны рассматривать только случай, когда имеется 1 единственный(!) корень. Разве не так?
Посмотрите внимательно, мы же сделали подстановку. Речь уже идёт о корнях уравнения t^2-3t+a-1=0, где t=5^x>0. Вот у этого уравнения должен быть один положительный корень или два корня, один из которых положителен, а драгой отрицателен или равен нулю, чтобы у исходного уравнения был один корень.
Добрый день!
В примере № 7 неправильно получен окончательный ответ. Допустим, а=0 (что включено в ваше решение). Получается, 618, a,-24
Добрый день! В примере 7 всё правильно, при a = 0 получается два корня 27/11 и 27/7.
Здравствуйте. Мне кажется, в решении примера 1 ошибка, которая, правда, не влияет на окончательный ответ, он верный, но тем не менее. При решении второго неравенства системы точка -3 получается выколотой, следовательно она не входит в решение этого неравенства. Первый промежуток ответа должен быть разбит этой точкой на два.
Здравствуйте, точка -3 не будет выколотой. Она входит в решение этого неравенства.
Да, нашел у себя ошибку. Точка -3 входит в решение. В задаче для самост. реш. №2 (у вас обозначено №3), мне кажется, ответ будет от 3/4 до 1 включительно. Ведь там корень существует только при а< либо =1.
Вы имеете ввиду задание для самостоятельного решения после примера 2? Там, где параметр b? Тогда нет. Возьмите, например, b=11/8 (это больше 1). Получится уравнение x-2 = корень(3x/4+1), у которого один корень x = 4.
Да, вы правы. Разобрался, нашел у себя ошибку.
Здравствуйте. В примере 4 ошибка. Если подставить точку минимума в функцию, получится 0
Здравствуйте. Нет, в примере 4 всё написано верно, ошибки нет.
F(-1)=3*(-1)^2+12*(-1)+9=0
Да. В примере 4 правильно, ошибся.Это в 3 ошиба
Это вы в производную подставляете, а не в функцию. Функция там f(x)=x(x+3)^2
Да, увидел. Спасибо
Очень!!! нерационально решен пример №2. Можно значительно проще. Значение квадратичной функции в 0 должно быть отрицательно: тогда и корня 2, и корни разных знаков, один из которых не удовлетворяет условию.
Да, есть и такое решение. Подобная задача с несколько иным условием уже мной решалась здесь (задача №8). Однако в Вашем решении не учтён ещё вариант с равным нулю дискриминантом и положительным корнем. Он всё равно остаётся. Так что на самом деле предложенное в этой статье альтернативное решение не сильно сложнее. Оба варианта решения имеют право на существование.
Скажите пожалуйста, как определить координаты вершины галочки, почему туда она смещается.
Абсцисса вершины галочки — это значение x, при котором модуль равен 0, ордината — значение y при найденном значении x.
Здравствуйте! Подскажите, как в Примере 4 получилось квадратное уравнение (из чего?) х2 + х +3а?
Здравствуйте! Для этого случая оба модуля раскрываются со знаком минус, поэтому и получается такое уравнение.
Здравствуйте. Почему во втором примере 1 включена в ответ? Ведь при 1 будет, что t=0, что противоречит условию введения этой переменной.
Здравствуйте, при a=1 получается t=0 (не подходит по ограничению) или t=3 (это подходит). Из второго решения получается единственный корень x.
Здравствуйте , а как например решать такую задачу
При каких значениях а система уравнений |х|+|у|=3 и у=х^2-а имеет ровно пять решений
Здравствуйте.В самост. заданиях 2 понял, что нужно найти при каких b знач по корнем >=0 но не могу получить правильный ответ
Куча косяков
Назовите хоть один
Сергей Валерьевич, можете, пожалуйста, написать подсказку к задаче для самостоятельного решения №2?