Вступительный экзамен в гимназию МГУ 2021 года

Среда, 26 января, 2022

Это вторая статья из цикла, посвященного подготовке к поступлению в Университетскую гимназию МГУ. Напоминаю, что специально для тех, кто самостоятельно готовится к вступительному экзамену в гимназию МГУ, я запустил новый телеграмм-канал (https://t.me/msu_gymn), в котором публикую варианты прошлых лет с подробными решениями всех заданий. Одну из задач каждого варианта я разбираю на своём Youtube-канале. Остальные решения выкладываю в Телеграмме и здесь на сайте.

Так что подписывайтесь на мой Youtube-канал, если ещё не подписаны, а также на мой новый канал в Телеграмме, чтобы ничего не пропустить. А сегодня у нас на очереди вариант реального вступительного экзамена в гимназию МГУ за 2021 год для инженерного и естественнонаучного направлений.

Разбор реального вступительного экзамена в гимназию МГУ за 2021 год

Задание 1. Решите неравенство:

$|x-4|-3x^2\geqslant 0$

1) Для $x\geqslant 4$ раскрываем модуль со знаком плюс:

$x-4-3x^2\geqslant 0$

$3x^2-x+4\leqslant 0$

Полученное неравенство не имеет решений, так как дискриминант соответствующего квадратного уравнения отрицателен, а ветви соответствующей параболы направлены вверх.

2) Для $x < 4$ раскрываем модуль со знаком минус:

$-x+4-3x^2\geqslant 0$

$3x^2+x-4 \leqslant 0$

$-\dfrac{4}{3}\leqslant x\leqslant 1$

Все точки в полученном промежутке удовлетворяют условию $x < 4$ .

Ответ: $x\in\left[-\dfrac{4}{3};1\right]$ .

Задание 2. Решите систему уравнений:

$\begin{cases} x^2-x+1 = y \\ y^2-y+1=x \end{cases}$

Перепишем систему в другом виде:

$\begin{cases} x^2+1 = y + x \\ y^2+1=x+y \end{cases}$

То есть $x^2+1 = y^2+1$ , что верно при $y = x$ или при $y = -x$ .

Для первого случая получаем:

$x^2+1 = x + x$

$x^2-2x+1 = 0$

$(x-1)^2 = 0$

$x = 1$

Для второго случая получаем:

$x^2-x+1 = -x$

$x^2 + 1 = 0$

Последнее уравнение не имеет решений.

Итак, получается у системы есть только одно решение $(1;1)$ .

Ответ: $(1;1)$ .

Задание 3. Сторона ромба равна 4, а угол при вершине тупого угла 150 градусов. Найдите расстояние от центра ромба до его стороны.

Изобразим ситуацию на рисунке:

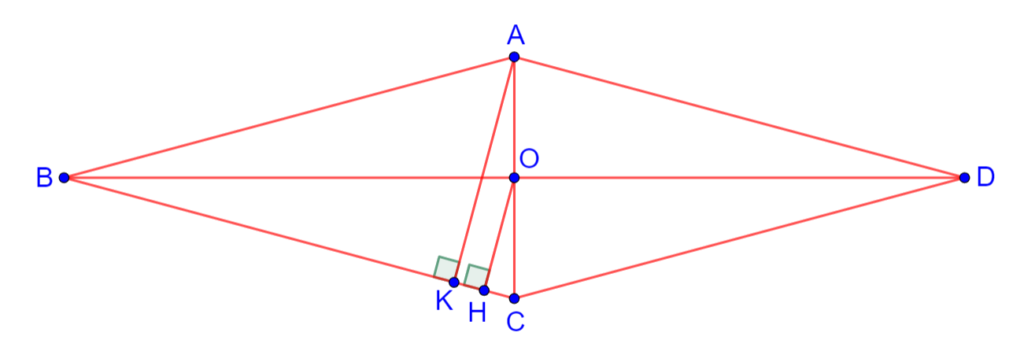
Так как прямые AD и BC параллельны, то $\angle B + \angle A = 180^{\circ}$ , так как эти углы являются односторонними при параллельных прямых. Значит, $\angle B = 30^{\circ}$ . Тогда в прямоугольном треугольнике ABK против этого угла лежит катет AK, который равен половине гипотенузы AB, то есть AK = 2.

Так как в ромбе, как в любом параллелограмме, диагонали точкой пересечения делятся пополам, то OH является средней линией треугольника AKC. Значит, $OH = \dfrac{1}{2}\cdot AK = 1$ .

Ответ: 1.

Задание 4. При вращении двух колёс, соединённых ременной передачей, меньшее колесо за 1 минуту делает на 90 оборотов больше, чем другое. Время, за которое каждое колесо делает 9 оборотов, отличается на 1 секунду. Сколько оборотов делает каждое колесо за 1 минуту?

Пусть одно колесо делает $x$ оборотов в минуту, а второе колесо делает $x+90$ оборотов в минуту. Тогда первое колесо делает 9 оборотов за $\dfrac{9}{x}$ минут, а второе колесо делает 9 оборотов за $\dfrac{9}{x+90}$ минут. Так как время одного колеса отличается от времени другого на 1 с, то есть на $\dfrac{1}{60}$ минуты, то имеет место уравнение:

$\dfrac{9}{x}-\dfrac{9}{x+90} = \dfrac{1}{60}$

$\dfrac{9\cdot 60(x+90)-9\cdot 60x-x(x+90)}{60x(x+90)} = 0$

$x^2+90x-48600=0$

Полученное уравнение имеет один положительный корень: $x = 180$ . То есть первое колесо делает 180 оборотов в минуту, а второе колесо делает 270 оборотов в минуту.

Ответ: 180 и 270.

Задание 5. Найдите радиус окружности, описанной около равнобедренного треугольника ABC, если радиус вписанной окружности равен 4.5, а длина медианы, проведённой к основанию, равна 12.

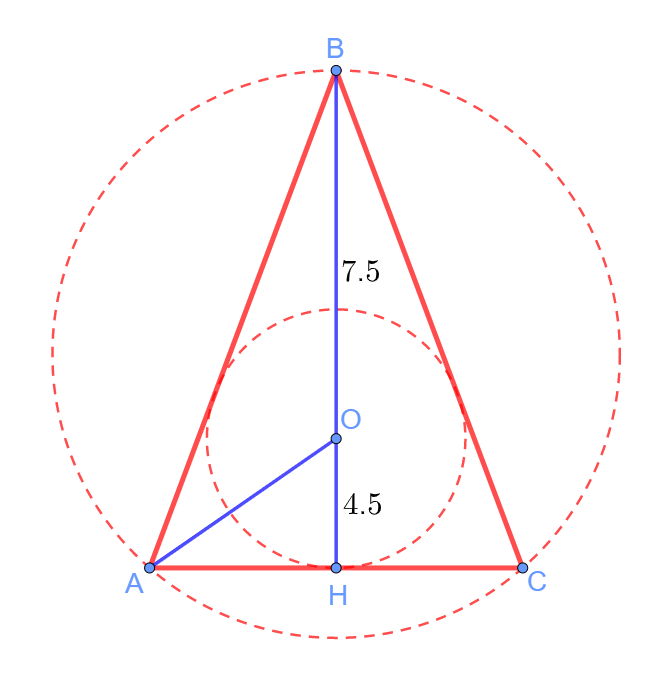
Изобразим ситуацию на рисунке:

Пусть AB = BC = a и AH = HC = b. Заметим, что AO — биссектриса угла A, так как центр вписанной окружности лежит в точке пересечения биссектрис треугольника. Тогда по свойству биссектрисы получаем, что $\dfrac{BO}{OH} = \dfrac{AB}{AH}$ , то есть $\dfrac{a}{b} = \dfrac{7.5}{4.5} = \dfrac{5}{3}$ . То есть $a = \dfrac{5}{3} b$ . Но по теореме Пифагора для треугольника ABH мы получаем:

$a^2 = 12^2 + b^2$

$\dfrac{25}{9}\cdot b^2 = 144 + b^2$

$b = 9$

То есть стороны треугольника ABC равны 15, 15 и 18, а площадь равна $S = \dfrac{1}{2}\cdot BH\cdot AC = 108$ . Теперь используем формулу $S = \dfrac{abc}{4R}$ , откуда находим, что $R = \dfrac{abc}{4S} = 9.375$ .

Ответ: 9.375.

Задание 6. Найдите множество значений функции $y = ax^2+a^2x-8x+2$ , если известно, что графиком функции является парабола, ветви которой направлены вниз, а прямая $x = 1$ является её осью симметрии.

Перепишем функцию в виде: $y = ax^2+(a^2-8)x+2$ . Так как известно, что графиком данной функции является парабола, ветви которой направлены вниз, то $a<0$ . Поскольку прямая $x = 1$ является осью симметрии этой параболы, то абсцисса вершины этой параболы равна $x_0 = 1$ . Но $x_0 = -\dfrac{b}{2a} = \dfrac{8-a^2}{2a}$ . Тогда имеет место уравнение:

$\dfrac{8-a^2}{2a} = 1$

$a^2 +2a - 8 = 0$

У последнего уравнения есть только один отрицательный корень $a = -4$ . Итак, функция имеет вид: $y = -4x^2 +8x+2$ . Её значение в вершине равно $y_0 = 6$ . Значит, область значений $E(y) = (-\infty; 6]$ .

Задание 7. На новом станке рабочий за 1 час обрабатывает целое число деталей, большее 8, а на старом станке на 3 детали меньше. Один рабочий на новом станке выполняет заказ за целое число часов, а двое рабочих, работая одновременно на старых станках, выполняют такой же заказ на 1 час быстрее. Определите, сколько деталей в заказе, если известно, что производительность рабочих одинакова.

Пусть на новом станке рабочий изготавливает $x > 8$ деталей в час. Тогда на втором станке рабочий изготавливает $x - 3$ детали в час. Пусть в заказе $N$ деталей. Тогда один рабочий выполняет заказ на новом станке за $\dfrac{N}{x}$ часов, причём это целое число. Тогда двое рабочих выполняют заказ на старых станках за $\dfrac{N}{2(x-3)}$ часов, что на 1 час меньше. Тогда имеет место равенство:

$\dfrac{N}{x} - \dfrac{N}{2(x-3)} = 1$

$N = \dfrac{6x-2x^2}{6-x}$

$N = 2x+6 + \dfrac{36}{x-6}$

Так как $x > 8$ , то $x - 6 > 2$ . Значит, для целых N возможно только, если:

1) $x - 6 = 3$ , то есть $x = 9$ и $N = 36$ , но тогда $\dfrac{N}{x} = 4$ является целым, то есть подходит.

2) $x - 6 = 4$ , то есть $x = 10$ и $N = 35$ , но тогда $\dfrac{N}{x}$ не является целым, то есть не подходит.

3) $x - 6 = 6$ , то есть $x = 12$ и $N = 39$ , тогда $\dfrac{N}{x}$ не является целым, то есть не подходит.

4) $x - 6 = 9$ , то есть $x = 15$ и $N = 40$ , но тогда $\dfrac{N}{x}$ не является целым, то есть не подходит.

5) $x - 6 = 12$ , то есть $x = 18$ и $N = 45$ , но тогда $\dfrac{N}{x}$ не является целым, то есть не подходит.

6) $x - 6 = 18$ , то есть $x = 24$ и $N = 56$ , но тогда $\dfrac{N}{x}$ не является целым, то есть не подходит.

7) $x - 6 = 36$ , то есть $x = 42$ и $N = 91$ , но тогда $\dfrac{N}{x}$ не является целым, то есть не подходит.

Ответ: 36.

Вот такой вариант по математике был на вступительном экзамене в гимназию МГУ в 2021 году. Полный разбор варианта представлен также на моём Телеграмм-канале. Там же вы найдёте и другие варианты вступительных экзаменов в гимназию МГУ с подробными решениями.

Так что тренируйтесь, это очень хорошая возможность для самостоятельной подготовки. Ну а если вам требуется помощь профессионального репетитора, специализирующегося на подготовке к поступлению в гимназию МГУ, обращайтесь ко мне. У меня в этом очень большой опыт. Многие мои ученики успешно справились с вступительными испытаниями и стали счастливыми учащимися этой замечательной гимназии. Мои контакты вы найдёте на этой странице. Успехов и Вам!

Материал подготовил репетитор по математике и физике Сергей Валерьевич

Метки: видеоуроки репетитора, гимназия МГУ, подготовка к вступительным экзаменам с репетитором
Опубликовано в категории Методическая копилка | Нет комментариев »

Вступительный экзамен в гимназию МГУ 2021 года

Разбор реального вступительного экзамена в гимназию МГУ за 2021 год

Добавить комментарий Cancel reply

Страницы

Понравился сайт?

Последние записи

Архив записей

Прочее