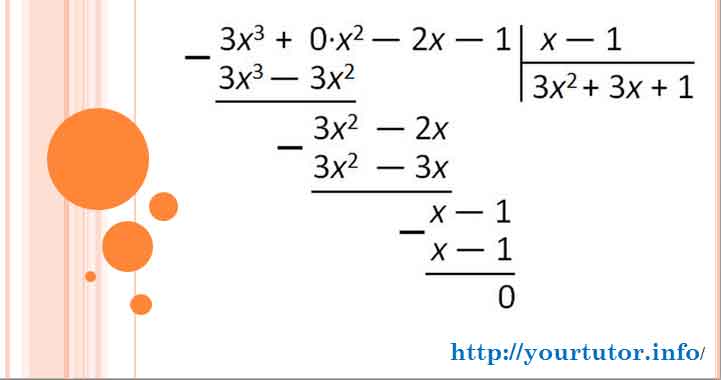 Статья о методах решения уравнений. Задач, которые связаны с решением уравнений, довольно много в вариантах ЕГЭ и ГИА по математике. Поэтому как репетитор по математике рекомендую освежить с памяти связанный с этим вопросом материал. К каждому разобранному в статье примеру прилагается аналогичное задание для самопроверки. Все свои вопросы вы можете смело задавать в комментариях. Ни один вопрос без ответа не останется. В статье также имеется видеоразбор одного из заданий.
Статья о методах решения уравнений. Задач, которые связаны с решением уравнений, довольно много в вариантах ЕГЭ и ГИА по математике. Поэтому как репетитор по математике рекомендую освежить с памяти связанный с этим вопросом материал. К каждому разобранному в статье примеру прилагается аналогичное задание для самопроверки. Все свои вопросы вы можете смело задавать в комментариях. Ни один вопрос без ответа не останется. В статье также имеется видеоразбор одного из заданий.
Основные методы решения уравнений
Решить уравнение значит найти все его корни или доказать, что их не существует. Стандартных методов решения уравнений много, нестандартных — еще больше. Последние подходят для решения небольшого количества (часто вообще одного) типа уравнений. При решении уравнений почти всегда приходится прибегать к тождественным преобразованиях алгебраических выражений. Поэтому целесообразно разобраться сперва с этим материалом, прежде чем переходить к решению уравнений. В данной статье разобраны в основном стандартные методы решения уравнений. Некоторые нестандартные методы кратко охарактеризованы в завершающей части статьи. Также на сайте есть отдельные статьи о решении тригонометрических, логарифмических и показательных уравнений, с которыми я также рекомендую читателю ознакомиться.
Метод разложения на множители
Суть данного метода в том, чтобы путем равносильных преобразований представить левую часть исходного уравнения, содержащую неизвестную величину в какой-либо степени, в виде произведения двух выражений, содержащих неизвестную величину в меньшей степени. При этом справа от знака равенства должен оказаться ноль. Проще всего уяснить эту идею на конкретном примере.
Решение. Осуществим разложение на множители (представим исходное выражение в виде произведения). Для этого вынесем переменную ![]() за скобки:
за скобки: ![]()
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Следовательно, ![]() или
или ![]() Из последнего уравнения получаем:
Из последнего уравнения получаем: ![]() или
или ![]()
Ответ: ![]() и
и ![]()
Задача для самостоятельного решения №1. Решите уравнение методом разложения на множители: ![]()
Показать ответ
Решение. Для разложения на множители используем прием деления многочленов столбиком (или, как еще иногда говорят, уголком). Несложно догадаться, что ![]() — корень многочлена
— корень многочлена ![]() Следовательно, по теореме Безу он без остатка делится на
Следовательно, по теореме Безу он без остатка делится на ![]() Осуществим это деление (см. подробнее в видеоуроке):
Осуществим это деление (см. подробнее в видеоуроке):
Таким образом ![]() То есть исходное уравнение принимает вид:
То есть исходное уравнение принимает вид:
![]()
Дискриминант первого квадратичного уравнения ![]() — отрицателен, поэтому корней у него нет. Из второго уравнения получается уже известный нам результат, что корень
— отрицателен, поэтому корней у него нет. Из второго уравнения получается уже известный нам результат, что корень ![]() Это единственный корень уравнения.
Это единственный корень уравнения.
Ответ: ![]() .
.
Задача для самостоятельного решения №2. Решите уравнение методом разложения на множители: ![]()
Показать ответ
Метод замены переменной
Цель данного метода в том, чтобы удачным образом заменить сложное выражение, содержащее неизвестную величину, новой переменной, в результате чего уравнение принимает более простой вид. Далее полученное уравнение решается относительно новой переменной, после чего происходит возврат к исходной переменной. Все эти идеи проще осознать на конкретном примере.
Решение. Такие уравнения называются биквадратными. Перепишем его в виде: ![]() Введем новую переменную
Введем новую переменную ![]() Тогда исходное уравнение примет следующий простой вид:
Тогда исходное уравнение примет следующий простой вид: ![]() Решая полученное квадратичное уравнение, получаем, что
Решая полученное квадратичное уравнение, получаем, что ![]() или
или ![]()
Возвращаемся теперь к старой переменной (обратная замена): ![]() или
или ![]() Решений у первого уравнения нет, поскольку не существует такого действительного числа, квадрат которого был бы отрицателен. Второе уравнение имеет два корня
Решений у первого уравнения нет, поскольку не существует такого действительного числа, квадрат которого был бы отрицателен. Второе уравнение имеет два корня ![]()
Ответ: ![]()
Задача для самостоятельного решения №3. Решите уравнение методом замены переменной: ![]()
Показать ответ
![]()
Решение. Обращаем внимание на то, что ![]() не является корнем данного уравнения. Следовательно, без потери или приобретения лишних корней можно разделить числитель и знаменатель обеих дробей на
не является корнем данного уравнения. Следовательно, без потери или приобретения лишних корней можно разделить числитель и знаменатель обеих дробей на ![]() Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
![]()
Введем новую переменную: ![]() Тогда уравнение примет вид:
Тогда уравнение примет вид:
![Rendered by QuickLaTeX.com \[ \frac{4}{t-8}+\frac{3}{t-10} = 1\Leftrightarrow \frac{t^2-25t+144}{(y-8)(y-10)} = 0. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-5f93daae7b3c8a5fa32b7591a6b3aca6_l3.png)
Дробь равна нулю, если нулю равен ее числитель, а знаменатель при этом не равен нулю. То есть уравнение равносильно следующей системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}t^2-25+144 = 0, \\ t\ne 8,\\ t\ne 10\end{cases}\Leftrightarrow \begin{cases}\left[\begin{array}{l} t = 16, \\ t =9, \end{array}\right. \\ t\ne 8,\\ t\ne 10\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ed0cea315f9850dd60c6b3d1bf6d373c_l3.png)
Итак, ![]() или
или ![]() Переходя к обратной подстановке, получаем:
Переходя к обратной подстановке, получаем:
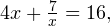 что при
что при 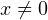 равносильно уравнению
равносильно уравнению 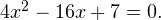 Откуда
Откуда 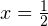 или
или 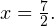
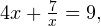 что при
что при 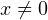 равносильно уравнению
равносильно уравнению 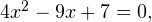 у которого решений нет, поскольку его дискриминант отрицателен.
у которого решений нет, поскольку его дискриминант отрицателен.
Ответ: ![]() и
и ![]()
Задача для самостоятельного решения №4. Решите уравнение методом разложения на множители: ![]()
Показать ответ
Метод оценки области значений
Суть данного метода в сравнении областей значений выражений, входящих в уравнение. Часто такой анализ позволяет легко решать сложные уравнения, содержащие различные выражения (рациональные, тригонометрические, логарифмические, показательные и др.). Разберем это на конкретном примере.
Решение. Рассмотрим функцию ![]() Известно, что
Известно, что ![]() поэтому
поэтому ![]() Итак, функция
Итак, функция ![]() может принимать значения только из промежутка
может принимать значения только из промежутка ![]()
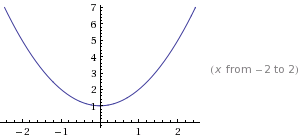
Рассмотрим теперь функцию ![]() Графиком данной функции является парабола, ветви которой направлены вверх, а вершина расположена в точке
Графиком данной функции является парабола, ветви которой направлены вверх, а вершина расположена в точке ![]()
То есть область значений данной функции (те значения, которые может принимать переменная ![]() ) представляет собой промежуток
) представляет собой промежуток ![]()
Таким образом выражения, стоящее справа и слева от знака равенства в исходном уравнении, могут оказаться равными, только если их значения окажутся равными 1, причем при одном и том же значении ![]() Непосредственной подстановкой убеждаемся, что это условие выполняется при
Непосредственной подстановкой убеждаемся, что это условие выполняется при ![]() Действительно,
Действительно, ![]() и
и ![]() При всех остальных значениях
При всех остальных значениях ![]() функция
функция ![]() больше 1 (см. график). Значит
больше 1 (см. график). Значит ![]() — единственный корень уравнения.
— единственный корень уравнения.
Ответ: 0.
Задача для самостоятельного решения №5. Решите уравнение с использованием метода оценки области значений: ![]()
Показать ответ
Нестандартные методы решения уравнений
![]()
Решение. Определим область допустимых значений (те значения, которые может принимать переменная ![]() в данном уравнении). Исходим из того, что подкоренное выражение не может быть отрицательным:
в данном уравнении). Исходим из того, что подкоренное выражение не может быть отрицательным:
![Rendered by QuickLaTeX.com \[ \begin{cases}2x-x^2+8\geqslant 0, \\ x^2-4x\geqslant 0, \\ -x-2\geqslant 0\end{cases}\Leftrightarrow\begin{cases}2x-x^2+8\geqslant 0, \\ x^2-4x\geqslant 0, \\ x\leqslant -2.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-1be607765444b4eb8936cc9d90924a82_l3.png)
Получается, что область допустимых значений содержит одно единственное значение ![]() Является ли это значение корнем уравнения, проще всего проверить прямой подстановкой:
Является ли это значение корнем уравнения, проще всего проверить прямой подстановкой:
![]()
![]()
Нет, не является.
Ответ: корней нет.
Задача для самостоятельного решения №6. Решите уравнение: ![]()
Показать ответ
![]()
Решение. Домножим уравнение на ![]() Вообще говоря, это преобразование не является равносильным, даже в области допустимых значений. Ведь могут найтись такие значения
Вообще говоря, это преобразование не является равносильным, даже в области допустимых значений. Ведь могут найтись такие значения ![]() при которых это выражение обратится в ноль. При таком преобразовании могут появиться лишние корни, поэтому полученные ответы нужно будет проверить непосредственной подстановкой. Но главное, что в результате такого преобразования не произойдет потери корней. Итак, преобразуем:
при которых это выражение обратится в ноль. При таком преобразовании могут появиться лишние корни, поэтому полученные ответы нужно будет проверить непосредственной подстановкой. Но главное, что в результате такого преобразования не произойдет потери корней. Итак, преобразуем:
![]()
![]()
![]()
![]()
Выражение во вторых скобках не может быть равно нулю. Действительно, оба корня по крайней мере неотрицательны, поэтому если к их сумме прибавить 1, получится положительное выражение. То есть остается, что ![]() или
или ![]() Непосредственной подстановкой убеждаемся, что это корень данного уравнения:
Непосредственной подстановкой убеждаемся, что это корень данного уравнения:
![]()
Ответ: 2.
Задача для самостоятельного решения №7. Решите уравнение: ![]()
Показать ответ
![Rendered by QuickLaTeX.com \[ x^2+\frac{81x^2}{(9+x)^2} = 40. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-2e44c878d3c712e1f7b129cd34908d8d_l3.png)
Решение. В область допустимых значений уравнения не входит число -9. Введем новую переменную ![]() Тогда в области допустимых значений последнее выражение преобразуется к виду
Тогда в области допустимых значений последнее выражение преобразуется к виду ![]() или
или ![]() Тогда имеет место система уравнений:
Тогда имеет место система уравнений:
![Rendered by QuickLaTeX.com \[ \begin{cases}x^2+t^2=40, \\ 9(x-t)-xt=0\end{cases}\Leftrightarrow\begin{cases}(x-t)^2=40-2xt, \\ 9(x-t)-xt=0\end{cases}\Lefrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-3eedda8026f5ad0f30731944d9510608_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\begin{cases}x-t=-20, \\ xt=-180\end{cases} \\ \begin{cases}x-t=2, \\ xt=18\end{cases}\end{array}\right.\Leftrightarrow x = 1\pm\sqrt{19}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-484ef31cadc4f91559bf9903965d4a5e_l3.png)
Ответ: ![]()
Задача для самостоятельного решения №8. Решите уравнение ![]()
Показать ответ
Вопрос методов решения уравнений изложенным в статье материалом, конечно, не исчерпывается. Существуют десятки других методов. Существуют также совершенно уникальные уравнения, для которых имеются свои собственное методы решения. Так что научиться здесь можно еще очень и очень многому. Самым хорошим помощником в этот деле для вас станет профессиональный репетитор по математике. Учите математику, сдавайте на отлично выпускные экзамены, поступайте в престижные вузы. Удачи вам!
Сергей Валерьевич
Частный преподаватель по математике