Решение задач контрольной работы по теории вероятностей

Вторник, 1 мая, 2012

Время от времени посетители сайта, узнав, что я являюсь действующим сотрудником МПГУ (Московского Педагогического Государственного Университета) и непосредственно связан с преподаванием физики в этом вузе, задают мне вопрос, занимаюсь ли я решением контрольных работ для студентов. Иногда этот вопрос звучит в более «мягкой» форме, а именно, осуществляю ли я помощь в выполнении контрольных работ по физике и математике для студентов вузов. Как бы то ни было, смысл остается тем же. Отвечаю вам на этот вопрос, уважаемые читатели.

Я являюсь действующим репетитором по физике и математике в Москве и занимаюсь в основном подготовкой школьников к сдаче ГИА и ЕГЭ по физике и математике. Однако, иногда (в случае наличия свободного времени) из интереса к вузовскому курсу математики я могу помочь студентам при выполнении контрольных работ по физике и математике (конкретно, по общей физике, классической механике и электродинамике, алгебре и геометрии, математическому анализу, теории вероятностей и математической статистике). Решил сегодня поделиться с вами одной из последних контрольных работ по дисциплине «Теория вероятностей» для II курса Московского отделения Всероссийского Заочного Финансово-Экономического Института (ВЗФЭИ).

Задача 1. Из 40 вопросов курса высшей математики студент знает 32. На экзамене ему случайным образом предлагаются два вопроса. Какова вероятность того, что студент ответит правильно:

хотя бы на один вопрос;
на оба вопроса?

Решение. Более подробно о решении элементарных задач по теории вероятностей читайте в статье «Задачи на вероятность из ЕГЭ». Под случайным событием в данной задаче понимается получение студентом двух вопросов на экзамене. Вопросы повторяться не могут и порядок их следования в билете не важен. Тогда общее число возможных исходов данного события определяется число сочетаний из 40 элементов по 2 и вычисляется по формуле:

$C_{40}^2 = \frac{40!}{2!\cdot (40-2)!} = \frac{39\cdot 40}{2} = 780.$

а) Рассчитаем вероятность того, что студенту попадется в билете два вопроса из тех, которые он не знает. Вновь имеем дело с сочетаниями 8 элементов по 2, число которых определяется по формуле:

$C_8^2=\frac{8!}{2!\cdot (8-2)!} = \frac{7\cdot 8}{2} = 28.$

Тогда вероятность такого события равна $\frac{28}{780} = \frac{7}{195}.$ Тогда вероятность противоположного события, заключающегося в том, что студенту попадется хотя бы один вопрос, который он знает, равна: $1-\frac{7}{195} = \frac{188}{195}.$

б) Ищем теперь вероятность того, что студенту попадутся оба вопроса из тех, что он знает. Имеем дело с сочетаниями из 32 элементов по 2, число которых определяется по формуле:

$C_{32}^2 = \frac{32!}{2!\cdot (32-2)!} = \frac{31\cdot 32}{2} = 496.$

Тогда вероятность этого события равна $\frac{496}{780} = \frac{124}{195}.$

Задача 2. При высаживании рассады помидоров только 80% приживаются. Найти вероятность того, что из 6 высаженных кустов приживутся не менее 5?

Решение. Искомую вероятность ищем по формуле Бернулли. Вероятность того, что событие наступит $k$ раз в $n$ независимых испытаниях равна $P_{k,n}=C_n^k p^k q^{n-k},$ здесь $p$ — вероятность наступления отдельного события (в нашем случае $p=0,8),$ $q$ — вероятность того, что это событие не наступит в единичном исследовании (в нашем случае $q = 1-p = 0,2).$ Ищем вероятность того, что приживется 5 или 6 кустов, то есть искомая вероятность равна:

$P_{5,6}+P_{6,6} = C_6^5\cdot 0,8^5\cdot 0,2^{6-5}+C_6^6\cdot 0,8^6\cdot 0,2^{6-6} =$

$=6\cdot 0,32768\cdot 0,2+0,262144 = 0,65536.$

Задача 3. Человек, проходящий мимо киоска, покупает газету с вероятностью 0,2. Найти вероятность того, что среди 400 человек, прошедших мимо киоска в течение часа:

купят газету 90 человек;
не купят газету от 300 до 340 человек (включительно).

Решение.

а) Имеем $m=90,$ $n=200>100,$ $q = 1-0,2 = 0,8$ , тогда $npq = 400\cdot 0,2\cdot 0,8 = 64>20,$ следовательно в расчетах можно использовать локальную и интегральную теоремы Муавра-Лапласа.

$x_m = \frac{m-n\cdot p}{\sqrt{npq}} = \frac{90-0,2\cdot 400}{\sqrt{400\cdot 0,2\cdot 0,8}} = 1,25.$

$f(x_m) = f(1,25) = 0,1826.$

Искомая вероятность равна:

$P_{400}(90) = \frac{1}{\sqrt{npq}}\cdot f(x_m) = \frac{1}{8}\cdot 0,1826 = 0,0228.$

б) Ищем вероятность того, что газеты не купят, поэтому в данном случае $n = 400,$ $p=0,8,$ $q = 1-0,8 = 0,2.$ Получаем тогда:

$x_1 = \frac{a-np}{\sqrt{npq}} = \frac{300-400\cdot 0,8}{\sqrt{400\cdot 0,8\cdot 0,2}} = -2,5$

$x_2 = \frac{b-np}{\sqrt{npq}} = \frac{340-400\cdot 0,8}{\sqrt{400\cdot 0,8\cdot 0,2}} = 2,5.$

Тогда получаем, что искомая вероятность равна (см. таблицу значений функции Лапласа):

$p = \frac{1}{2}\left[\Phi(2,5)-\Phi(-2,5)\right] = \Phi(2,5) = 0,98758.$

Задача 4. Пульт охраны связан с тремя охраняемыми объектами. Вероятность поступления сигнала с этих объектов составляет соответственно 0,2, 0,3 и 0,6. Составить закон распределения случайной величины: числа объектов с которых поступит сигнал. Найти математическое ожидание и дисперсию этой случайной величины.

Решение. Введем обозначения $A,\, B,\, C$ — события, заключающиеся в поступлении сигналов с первого, второго и третьего объектов соответственно. Тогда:

$P(0) = P(\overline{A}\,\overline{B}\,\overline{C}) = 0,8\cdot 0,7\cdot 0,4 = 0,224;$

$P(1) = P(A\overline{B}\,\overline{C}+\overline{A}B\overline{C}+\overline{A}\,\overline{B}C) = 0,2\cdot 0,7\cdot 0,4+$

$+0,8\cdot 0,3\cdot 0,4+0,8\cdot 0,7\cdot 0,6 = 0,488;$

$P(2) = P(AB\overline{C}+A\overline{B}C+\overline{A}BC) = 0,2\cdot 0,3\cdot 0,4+$

$+0,2\cdot 0,7\cdot 0,6+0,8\cdot 0,3\cdot 0,6 = 0,252.$

$P(3) = P(ABC) = 0,2\cdot 0,3\cdot 0,6 = 0,036.$

Контроль: $0,224+0,488+0,252+0,036 = 1.$

Закон распределения тогда принимает вид:

$x_i$	0	1	2	3
$p_1$	0,224	0,488	0,252	0,036

Математическое ожидание вычисляем по формуле:

$M(X) = \sum^{4}_{i=1} {x_ip_i}=0\cdot 0,224+1\cdot 0,488+$

$+2\cdot 0,252+3\cdot 0,036 = 1,1.$

Дисперсию вычисляем по формуле:

$D(X) = M\left(X^2\right) - \left[M(X)\right]^2=\sum^{4}_{i=1}{x^2_ip_i}-\left[M(X)\right]^2 =$

$= 0^2\cdot 0,224+1^2\cdot 0,488+2^2\cdot 0,252+$

$+3^2\cdot 0,036 - 1,1^2 = 0,61.$

Задача 5. Плотность вероятности случайной величины $X$ имеет вид:

$\varphi(x) = \begin{cases} 0,\, x<1, \\ \frac{1}{4},\, 1\leqslant x\leqslant b, \\ 0, x>b.\end{cases}$

Найти по этом данным:

параметр $b$ ;
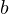математическое ожидание и дисперсию случайной величины $Х;$
функцию распределения $F(x)$ .

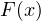Оценить с помощью неравенства Чебышева вероятность того, что случайная величина принимает значения на промежутке $[1,5; 4,5]$ . Вычислить эту вероятность с помощью функции распределения. Объяснить различие результатов.

Решение.

а) В соответствии с основным свойством плотности вероятности, несобственный интеграл от плотности вероятности в пределах от $-\mathcal{1}$ до $+\mathcal{1}$ равен единице, то есть в нашем случае получаем:

$\int\limits_{-\mathcal{1}}^{+\mathcal{1}} \varphi (x) \,dx = \int\limits_1^b \frac{1}{4}\,dx = \frac{1}{4}(b-1) = 1\Rightarrow b = 5.$

Итак, функция плотности вероятности случайной величины $X$ имеет вид:

$\varphi(x) = \begin{cases} 0,\, x<1, \\ \frac{1}{4},\, 1\leqslant x\leqslant 5, \\ 0, x>5.\end{cases}$

б) Математическое ожидание непрерывной случайной величины определяется в нашем случае по формуле:

$M(X) = \int\limits_{-\mathcal{1}}^{+\mathcal{1}} x\cdot \varphi (x) \,dx = \int\limits_1^5 \frac{1}{4}x\, dx = \Bigl. \frac{x^2}{8} \Bigr|_1^5 = 3.$

Дисперсия непрерывной случайной величины вычисляется в данном случае по формуле:

$D(X) = \int\limits_{-\mathcal{1}}^{+\mathcal{1}} x^2\cdot \varphi (x) \,dx - \left[M(X)\right]^2 = \int\limits_1^5 \frac{1}{4}x^2\, dx - 3^2=$

$=\Bigl. \frac{x^3}{12} \Bigr|_1^5 - 9 = \frac{125}{12}-\frac{1}{12} - 9 = \frac{31}{3}-9=\frac{4}{3}.$

в) Функция распределения связана с плотностью вероятности следующим образом:

$F(x) = \int\limits_{-\mathcal{1}}^x \varphi (x) \,dx.$

Интегрируя, получаем:

$F(x) = \begin{cases}0,\, x<1, \\ \frac{1}{4}x-\frac{1}{4},\, 1\leqslant x\leqslant 5, \\ 1,\, x>5. \end{cases}$

С помощью неравенства Чебышева оценим, что случайная величина принимает значения, находящиеся в промежутке $[1,5;4,5]:$

$P(|x-a|\leqslant \varepsilon)\geqslant 1-\frac{D(X)}{\varepsilon^2}.$

В нашем случае получаем:

$P(|x-3|\leqslant 1,5) \geqslant 1-\frac{\left(\frac{4}{3}\right)^2}{1,5^2} = \frac{17}{81}.$

Это означает, что вероятность того, что наша случайная величина примет значение, находящееся в промежутке $[1,5;4,5]$ ограничена снизу значением $\frac{17}{81}.$

Оценим теперь эту же вероятность с помощью функции распределения:

$P = F(4,5)-F(1,5) =$

$=\frac{1}{4}\cdot 4,5-\frac{1}{4}-\left(\frac{1}{4}\cdot 1,5-\frac{1}{4}\right)=0,75.$

Полученные значения не совпадают, поскольку неравенство Чебышева дает лишь нижнюю оценку вероятности случайного события, а не точное значение этой вероятности.

Репетитор по физике и математике
Сергей Валерьевич
Читать @Sergey_V_S

Метки: ответы на вопросы учеников, решение контрольных работ по математике
Опубликовано в категории Методическая копилка | 2 комментария »

Решение задач контрольной работы по теории вероятностей

Комментарии

Добавить комментарий Cancel reply

Страницы

Понравился сайт?

Последние записи

Архив записей

Прочее