Во время сдачи ЕГЭ по математике использование калькулятора, как известно, запрещено. Поэтому любой репетитор по математике всегда заставляет своих учеников считать все устно или на бумаге. Но время от времени встречаются задачи, при решении которых требуется извлекать квадратные корни из достаточно больших чисел, и на ЕГЭ по математике такие задачи тоже есть. С проблемой нахождения алгоритма вычисления квадратного корня из вещественного числа читатель может столкнуться (помимо ЕГЭ по математике) на различного рода математических конкурсах и олимпиадах. Итак, как найти квадратный корень без использования калькулятора?
Как репетитор по физике и математике, занимающийся подготовкой к ЕГЭ и ГИА, предлагаю вашему вниманию один действенный алгоритм, не претендующий на максимальную эффективность, но работающий безотказно с любыми вещественными числами. Приведенный метод может со временем стать столь же известным, как, к примеру, метод умножения двух чисел «столбиком», ведь он во многом на него похож.
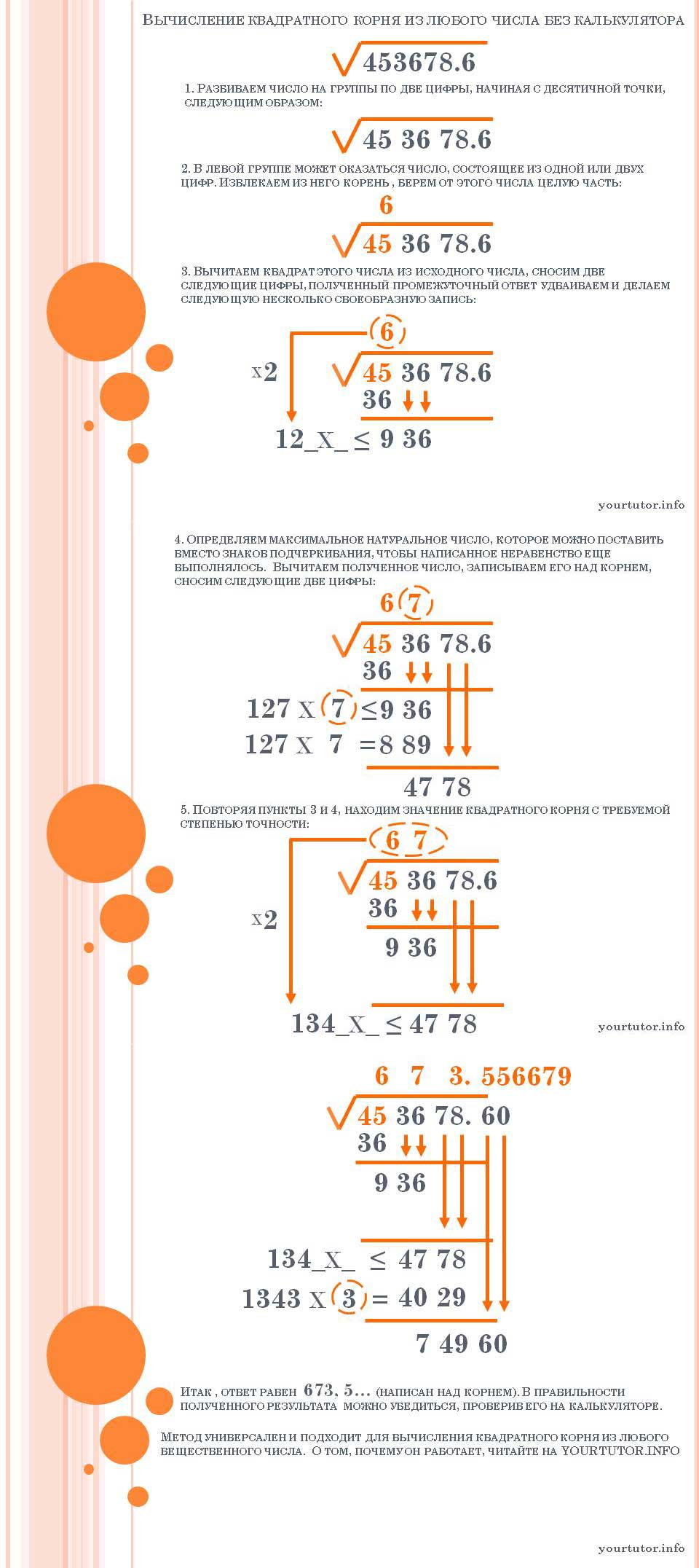
Вот наглядная схема алгоритма вычисления квадратного корня из любого числа без использования калькулятора (кликабельно):
Алгоритм вычисления квадратного корня из любого вещественного числа без использования калькулятора
Однако, вопрос о том, почему данный алгоритм работает, остается пока открытым. Для того, чтобы разобраться в этом, возьмем, для примера, число, цифрами которого являются 
и 
То есть само число имеет вид 
Пусть корнем будет число 
, состоящее из цифр 
и 
То есть 
Выполним «столбиком» умножение 
Последовательно:
![\[ 10x\cdot 10x = 100x^2,\, 2\cdot x\cdot 10y=20xy,\, y\cdot y = y^2.\]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-06e4c59360c0873f2ddf3abb30e96c67_l3.png "Rendered by QuickLaTeX.com")
То есть:
![\[ \overline{abcd} = 100x^2+20 xy+y^2.\]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-3dc210e5f487a90964d9b256fcba8dc4_l3.png "Rendered by QuickLaTeX.com")
Проанализировав это разложение, понимаем, что разделяя число 
на пары 
и 
числу в первой паре мы ставим в соответствие число, содержащееся в 
Иначе говоря, квадратный корень из числа 
округленный до нижнего целого числа, есть 
Теперь, зная значение 
для нахождения 
необходимо вычислить значение выражения 
или, что то же самое, значение выражения 
Поразмыслив над этим, понимаем, что в этом, собственно, и состоит суть действия, совершаемого при подборе числа, которое необходимо подставить на четвертом шаге алгоритма вместо знаков подчеркивания. Таким образом мы находим Зная и 
знаем 
Такой подход может быть обобщен на случай любого количества разрядов в исходном числе. Если корень не является рациональным, вычисления могут продолжаться сколь угодно долго (с любой необходимой степенью точности). Вот такой простой алгоритм. Запомните его, возможно, он пригодится вам при сдаче ЕГЭ по математике.
Репетитор по математике
Сергей Валерьевич
© Марк Твен
Способ не очень. Используется небезызвестный метод Ньютона, он же метод отрезков, но вычисления намного сложнее.
Не согласен, что метод Ньютона будет проще с точки зрения вычислений. Навскидку два аргумента.
1) Метод Ньютона быстро сходится только если начальное приближение выбрано достаточно близко. В данном примере, если за начальное приближение взять x_1 = 600, то для получения точного третьего знака потребуется 3 итерации. А три раза без калькулятора посчитать выражение 0.5*(x_k+453678.6/x_k) по-моему сложнее, чем то, что предлагается в данном способе.
2) Сложно оценить погрешность вычислений. После каждой итерации не понятно сколько значащих цифр имею действительно правильное значение. В данном методе в любой полученной цифре можно быть уверенным и решать с любой требуемой степенью точности.
Метод Ньютона хорош для машинных вычислений. «На бумаге» им по-моему не очень удобно пользоваться.
Можете объяснить дураку две вещи:
1)откуда взялось 10x
2)почему в первом действии 10x, а в во втором действии 10y
x — это первая цифра двузначного числа, то есть, например 2 в числе 23. Нам в первом действии нужна не 2, а 20, поэтому мы пишем 10x. 10y по той же причине появляется. Умножьте на бумаге xy*xy столбиком, станет понятнее.
Если xy — корень из abcd, то (xy)^2 = adcd. В статье написано, что xy^2 = abcd (т.е. x в квадрат не возводится).
Здесь запись xy не означает, что x умножается на y, здесь это буквенная запись двузначного числа. Вы же не пишете (32)^2, если хотите узнать квадрат 32, Вы пишете 32^2.
Если бы над числами abcd и xy стояли черточки, было бы понятней.
Действительно, поставил черточки, стало выглядеть понятнее. Спасибо Вам за рекомендацию!
Всё супер! Спасибо за помощь!
Хороший метод, спасибо, но меня немного смущает подбор. Хотя и в обычном методе деления в столбик требуется подбор, но там все-таки немного проще — нужно на каждом шаге подбирать только один множитель (здесь — два множителя).
Вместе с делением в столбик метод Ньютона подходит для ручных вычислений.
Хотя я предпочитаю модификацию с использованием арифметического и гармонического среднего. Этот метод сходится всегда для любых начальных значений.
Подробности можно посмотреть здесь:
http://math.stackexchange.com/questions/1734978/computing-square-roots-with-arithmetic-harmonic-mean
Спасибо за ссылку и комментарий, соглашусь, что данный модифицированный метод тоже удобен для вычисления квадратных корней. Хотя для школьников, не знакомых с численными методами, привычнее, наверное, будет метод, предложенный в статье.
Спасибо за ответ. Я потренируюсь в Вашем методе, вполне возможно что он будет гораздо быстрее. Это как с делением в столбик — без тренировки тяжело.
Кстати о проверке результата — в методе приведенном мной верные знаки проверяются сравнением арифметического и гармонического средних, а в методе Ньютона можно также сравнивать x_n и а/x_n где а — число, из которого извлекаем корень. Так что тут не совсем безнадежное дело
А можно ли использовать метод Ньютона на ЕГЭ при решении алгебраических уравнений? Просто есть сомнения в виду того, что этот метод найден в Интернете и нужно доказать его и т.п.
В заданиях последней части ЕГЭ, где требуется привести полное решение, все прекрасно решается и без метода Ньютона. А в заданиях с кратким ответом, решать, понятно, можно как угодно.
Думаю, для этого способа, для нахождения второй (и следующих) цифр результата, можно взять число десятков «остатка», который получился после сноса грани (закрыть пальцем последнюю цифру), и разделить на удвоенную известную часть результата. Цифру, которая получилась, подставить в «формулу», которую обычно пишем слева. Если результат получился больше, чем надо (такое бывает часто) — надо взять цифру на один меньше.
Фактически это просто, чтобы избежать подбора, как я понимаю? Хотя и подбор тоже использовать не страшно, потому что при делении столбиком, например, он тоже используется.
Метод хорош для нахождения корня с небольшим количеством знаков(до 5-6).
Далее подсчет становится весьма тудозатратен.
Думаю, что лучше с этих пор перейти на метод Ньютона (он же Вавилонский), либо сразу с него начать.
СПАСИБО ОГРОМНОЕ
меня давно волновал вопрос о вычислении корня без калькулятора( я в 11 классе)
из иррациональных я научилась по-другому методу, но из таких…(не иррациональных)
прочитав ваш способ, я взяла большое число и … у меня получилось!!!
я в восторге…
правда, мне для решения достаточно посчитать с точностью до десятых ( в моей 17 задаче) , но я понимаю, что смогу и дальше ))))
решила пример я достаточно быстро)))
в общем, супер)))
В советском мультике «На задней парте» (в первой серии) данный способ упоминается.
В случае корня из 73485,48 метод не сработал на третьем знаке после запятой: метод дает единицу, а по факту двойка