Предлагаю вашему вниманию разбор репетиционного ЕГЭ по математике, прошедшего в школах России 17 марта 2012 года. Задания приведены с достаточно подробными решениями и комментариями, а также ссылками на необходимую теоретическую информацию. Используя все это каждый читатель при желании сможет разобраться во всех деталях и нюансах решения. Однако, как репетитор по математике, в педагогических целях предлагаю вам сперва решить каждое задание самостоятельно, а затем сравнить свое решение с тем, что приведено здесь. Статья получилась сложной и большой, так что (совет репетитора по математике) если хотите добраться до конца, придется набраться терпения, оно вам очень понадобится, как впрочем и всегда при качественном изучении математики.
Решение задачи B1. Несложно посчитать, что всего на теплоходе находится ![]() человек. Делим
человек. Делим ![]() на
на ![]() , получаем
, получаем ![]() и
и![]() в остатке. Это означает, что потребуется
в остатке. Это означает, что потребуется ![]() спасательных шлюпок, чтобы разместить в них
спасательных шлюпок, чтобы разместить в них ![]() человек. Оставшиеся
человек. Оставшиеся ![]() человек разместятся в еще одной дополнительной спасательной шлюпке, которая будет заполнена не до конца. Всего, таким образом, потребуется
человек разместятся в еще одной дополнительной спасательной шлюпке, которая будет заполнена не до конца. Всего, таким образом, потребуется ![]() спасательных шлюпок. Ответ: 8.
спасательных шлюпок. Ответ: 8.
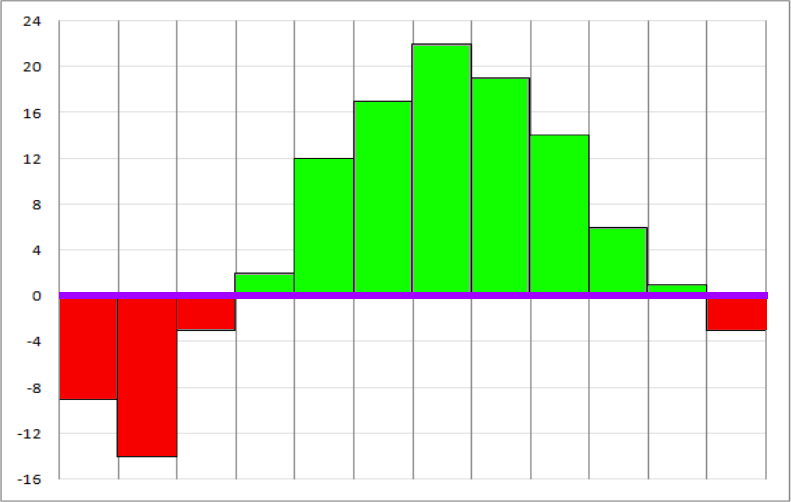
Решение задачи B2. Положительной среднемесячной температуре воздуха на диаграмме соответствуют зеленые столбики (они целиком лежат выше синей линии, соответствующей нулю градусов Цельсия). Отрицательной среднемесячной температуре воздуха на диаграмме соответствуют красные столбики (они целиком лежат ниже синей линии, соответствующей нулю градусов Цельсия). Красных столбиков на диаграмме четыре, а значит количество месяцев с отрицательной среднемесячной температурой воздуха равно четырем. Ответ: 4.
Решение задачи B3. Формулы для вычисления площади треугольников приведены в этой статье. Из всего их многообразия в данной задаче удобно использовать вот эту: ![]() (площадь треугольника
(площадь треугольника ![]() равна половине произведения его высоты
равна половине произведения его высоты ![]() на основание
на основание ![]() ).
).
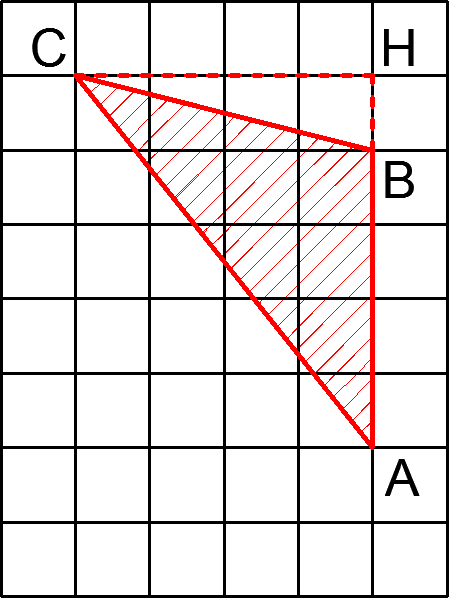
Основанием может служить любая сторона треугольника. В нашем примере в качестве основания удобно выбрать сторону AB, которая занимает 4 клеточки, а значит равна 4 см.
Высотой треугольника является перпендикуляр, опущенный из вершины треугольника на прямую, содержащую его основание. В данном случае это отрезок CH, который занимает 4 клеточки и равен поэтому 4 см.
В данном случае она расположена вне треугольника.
Итак, искомая площадь треугольника равна: ![]()
![]() квадратных сантиметров. Ответ: 8.
квадратных сантиметров. Ответ: 8.
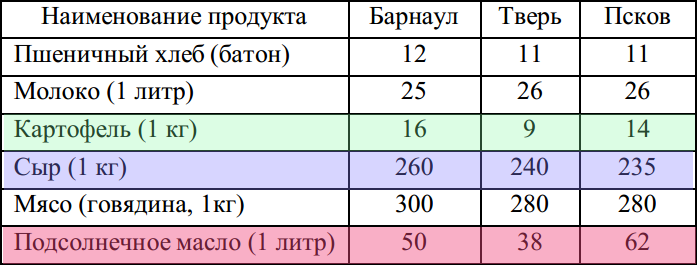
Решение задачи B4. Считаем стоимость такой покупки для каждого города в отдельности:
- Барнаул:
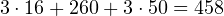 руб.
руб. - Тверь:
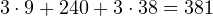 руб.
руб. - Псков:
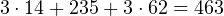 руб.
руб.
В Твери все это можно было купить в начале 2010 года за 381 руб. Ответ: 381.
Решение задачи B5. Корень из какого числа равен ![]() Очевидно, что из
Очевидно, что из ![]() поэтому
поэтому ![]() Переносим
Переносим ![]() в правую часть уравнения, меняя при этом знак
в правую часть уравнения, меняя при этом знак ![]() Получаем, что
Получаем, что ![]() Какое число нужно умножить на
Какое число нужно умножить на ![]() чтобы получилось
чтобы получилось ![]() Очевидно, что
Очевидно, что ![]() Ответ: 9.
Ответ: 9.
Решение задачи B6. Существует теорема, согласно которой сумма противоположных углов вписанного четырехугольника равна ![]() Это означает, что данные в условии углы в этом четырехугольнике не являются противоположными, так как их сумма
Это означает, что данные в условии углы в этом четырехугольнике не являются противоположными, так как их сумма ![]()
![]() Тогда два оставшихся угла данного четырехугольника равны соответственно
Тогда два оставшихся угла данного четырехугольника равны соответственно ![]() и
и ![]() Из них не сложно выбрать больший. Ответ: 128.
Из них не сложно выбрать больший. Ответ: 128.
Решение задачи B7. Используем основное тригонометрическое тождество: ![]() откуда получаем, что
откуда получаем, что ![]() Что нужно возвести в квадрат, чтобы получить
Что нужно возвести в квадрат, чтобы получить ![]() Либо
Либо ![]() либо
либо ![]() То есть либо
То есть либо ![]() либо
либо ![]() Какой же ответ выбрать?
Какой же ответ выбрать?
В условии дано, что угол ![]() то есть принадлежит третьей координатной четверти, где синус, как известно, отрицателен. То есть берем то, что с минусом. Ответ: -0,1.
то есть принадлежит третьей координатной четверти, где синус, как известно, отрицателен. То есть берем то, что с минусом. Ответ: -0,1.
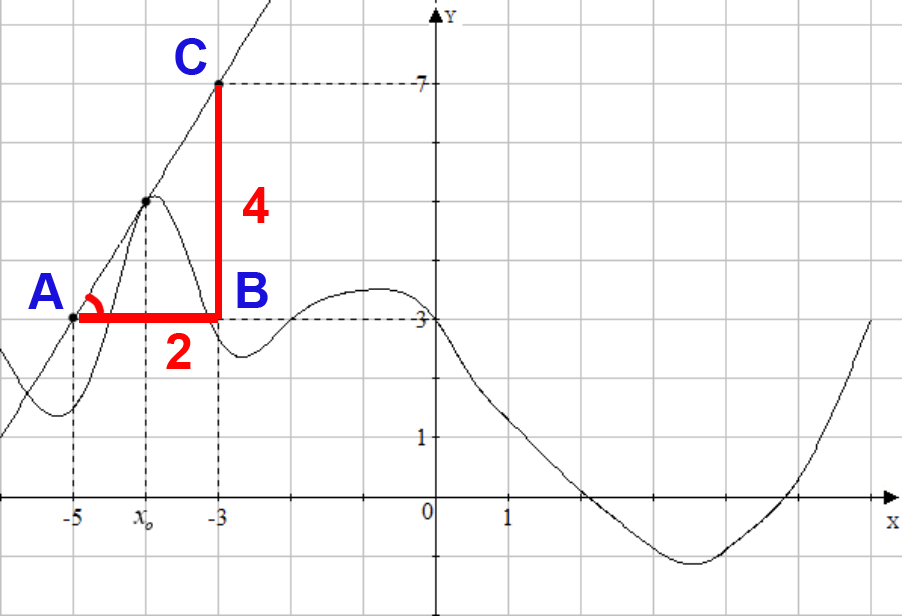
Решение задачи B8. Геометрический смысл производной состоит в том, что значение производной функции в точке численно равно тангенсу угла между касательной к функции в данной точке и положительным направлением оси OX. То есть требуется найти ![]() в прямоугольном треугольнике ABC (см. рисунок).
в прямоугольном треугольнике ABC (см. рисунок).
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему, то есть в нашем случае ![]() По знаку производная в данной точке положительна, поскольку в окрестности этой точки исходная функция возрастает (следствие из теоремы Лагранжа). Ответ: 2.
По знаку производная в данной точке положительна, поскольку в окрестности этой точки исходная функция возрастает (следствие из теоремы Лагранжа). Ответ: 2.
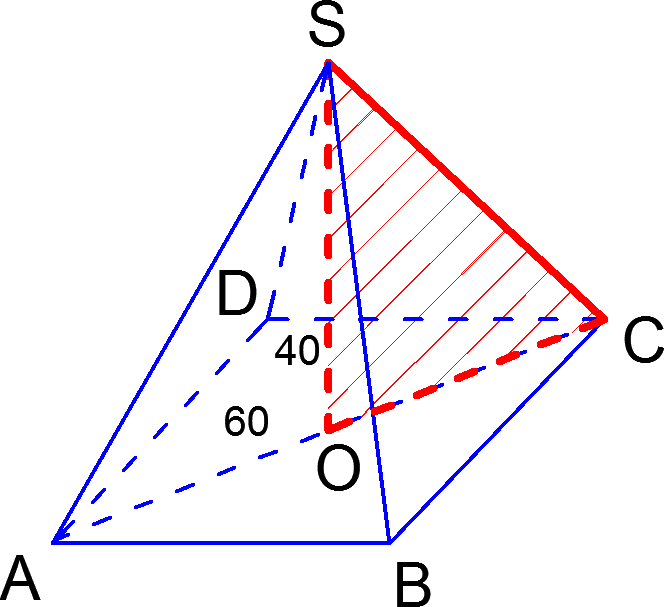
Решение задачи B9. ![]() . Действительно, поскольку
. Действительно, поскольку ![]() — правильная пирамида, то ее боковые ребра равны, то есть
— правильная пирамида, то ее боковые ребра равны, то есть ![]() . Это означает, что
. Это означает, что ![]() — равнобедренный треугольник. В нем
— равнобедренный треугольник. В нем ![]() является медианой, поскольку
является медианой, поскольку ![]() — центр основания. В равнобедренном треугольнике медиана, проведенная к основанию является высотой, значит
— центр основания. В равнобедренном треугольнике медиана, проведенная к основанию является высотой, значит ![]() .
.
![]() , так как
, так как ![]() — центр основания пирамиды. Тогда из теоремы Пифагора для прямоугольного треугольника
— центр основания пирамиды. Тогда из теоремы Пифагора для прямоугольного треугольника ![]() получаем
получаем ![]() Ответ: 50.
Ответ: 50.
Решение задачи B10. Подробно о том, как решаются задачи по теории вероятностей из ЕГЭ по математике, читайте в статье «Задачи на вероятность из ЕГЭ». Вероятность наступления случайного события определяется отношением числа благоприятных исходов к общему числу исходов эксперимента. Далее Р — выпадение решки, О — выпадение орла.
- Благоприятных исходов эксперимента: РРО, РОР, ОРР — три.
- Общее число исходов эксперимента: ООО, ООР, ОРО, РОО, ОРР, РРО, РОР, РРР — восемь.
Тогда искомая вероятность равна ![]() Ответ: 0,375.
Ответ: 0,375.
Решение задачи B11. Пусть начальная длина ребра куба была равна ![]() , тогда площадь каждой грани была равна
, тогда площадь каждой грани была равна ![]() (площадь квадрата равна квадрату его стороны), а вся площадь поверхности куба —
(площадь квадрата равна квадрату его стороны), а вся площадь поверхности куба — ![]() , поскольку всего у куба шесть граней. После увеличения длина каждого ребра куба стала равна
, поскольку всего у куба шесть граней. После увеличения длина каждого ребра куба стала равна ![]() , тогда площадь каждой грани стала равна
, тогда площадь каждой грани стала равна ![]() , а вся площадь поверхности куба —
, а вся площадь поверхности куба — ![]() .
.
Как определить во сколько раз увеличилась площадь поверхности куба? Очевидно, вычислив вот такое отношение: ![]() . То есть площадь поверхности куба увеличилась в 100 раз. Ответ: 100.
. То есть площадь поверхности куба увеличилась в 100 раз. Ответ: 100.
Решение задачи B12. Все сводится к подстановке в формулу численных значений и решению получившегося логарифмического уравнения. Более подробно о решении логарифмических уравнений и неравенств читайте в статье «Решение задач C3 ЕГЭ по математике — логарифмические уравнения и неравенства».
![]()
![]() л. Ответ: 2,5.
л. Ответ: 2,5.
Решение задачи B13. Пусть ![]() руб. — стоимость куртки,
руб. — стоимость куртки, ![]() руб. — стоимость рубашки,
руб. — стоимость рубашки, ![]() — искомое количество процентов. Тогда в соответствии с условием имеет место следующая система:
— искомое количество процентов. Тогда в соответствии с условием имеет место следующая система:
![Rendered by QuickLaTeX.com \[ \begin{cases} 7x = 0,91y, \\ 11x = y\cdot\frac{100+p}{100}.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-a2eb260a650feade650d0e2a79583518_l3.png)
Делением первого уравнения системы на второе получаем:
![]()
Ответ: 43.
Решение задачи B14. Действуем по алгоритму нахождения минимума/максимума функции одной переменной.
1. Находим производную функции. С правилами дифференцирования функций читатель может ознакомиться здесь.
![]()
![]()
![]()
2. Приравниваем к нулю и ищем нули производной.
![]()
Обе части уравнения можно разделить на ![]()
![]()
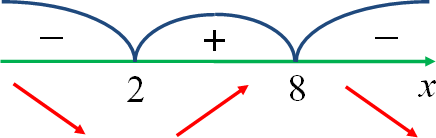
3. Наносим полученные точки на числовую прямую и определяем знаки производной функции на полученных промежутках.
Итак, в точке ![]() производная функции меняет свой знак с минуса на плюс, значит убывание исходной функции в этой точке сменяется ее возрастанием, то есть
производная функции меняет свой знак с минуса на плюс, значит убывание исходной функции в этой точке сменяется ее возрастанием, то есть ![]() — точка минимума исходной функции. Ответ: 2.
— точка минимума исходной функции. Ответ: 2.
а) Решите уравнение
![]()
![]()
![]()
б) Укажите все корни этого уравнения, принадлежащие отрезку ![]()
Решение задачи C1. Прибавим к обеим частям уравнения выражение ![]() далее упрощаем уравнение путем равносильных преобразований:
далее упрощаем уравнение путем равносильных преобразований:
![]()
![]()
![]()
![]()
Используем замену переменной: ![]() . Получаем следующее уравнение:
. Получаем следующее уравнение:
![]()
Возвращаемся к исходной переменной:
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l} 4^{\sin x} = 1, \\ 4^{\sin x} = 2 \end{array}\right.\Leftrightarrow \left[\begin{array}{l} 4^{\sin x} = 4^0, \\ 4^{\sin x} = 4^{\frac{1}{2}} \end{array}\right.\Leftrightarrow \left[\begin{array}{l} \sin x = 0, \\ \sin x = \frac{1}{2} \end{array}\right.\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-6ed82010c4a1329859acd3a280631b57_l3.png)
![]()
б) Осуществляем отбор решений. Изображаем полученные серии ответов на числовой окружности и выбираем те ответы, которые принадлежат данному в условии промежутку: ![]()

Точки на единичной окружности соответствуют полученным решениям, интересующий нас промежуток отмечен красным цветом
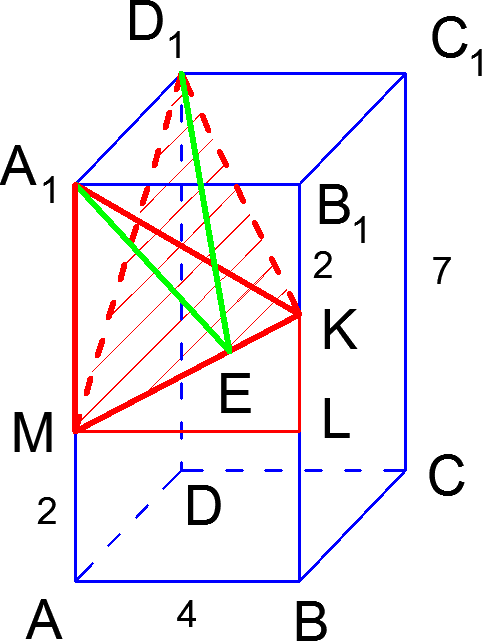
Решение задачи C2.
Поскольку ![]() — правильная пирамида, то
— правильная пирамида, то ![]() , и искомый угол будет равен углу между плоскостями
, и искомый угол будет равен углу между плоскостями ![]() и
и ![]() Угол между двумя плоскостями — это угол между перпендикулярами, проведенными в обеих плоскостях к линии их пересечения. Плоскости
Угол между двумя плоскостями — это угол между перпендикулярами, проведенными в обеих плоскостях к линии их пересечения. Плоскости ![]() и
и ![]() пересекаются по прямой
пересекаются по прямой ![]() Проведем высоту
Проведем высоту ![]() в треугольнике
в треугольнике ![]() Соединим точки
Соединим точки ![]() и
и ![]()
Докажем, что ![]() Действительно,
Действительно, ![]() — наклонная к плоскости
— наклонная к плоскости ![]() а
а ![]() — ее проекция на эту плоскость, так как
— ее проекция на эту плоскость, так как ![]() (призма правильная). Прямая
(призма правильная). Прямая ![]() лежит в плоскости
лежит в плоскости ![]() и перпендикулярна наклонной
и перпендикулярна наклонной ![]() по построению, а значит перпендикулярна и ее проекции
по построению, а значит перпендикулярна и ее проекции ![]() по теореме, обратной теореме о трех перпендикулярах. Итак,
по теореме, обратной теореме о трех перпендикулярах. Итак, ![]() и
и ![]() , следовательно,
, следовательно, ![]() — искомый угол между плоскостями.
— искомый угол между плоскостями.
Отрезок ![]() отрезок
отрезок ![]()
![]() Из теоремы Пифагора для прямоугольного треугольника
Из теоремы Пифагора для прямоугольного треугольника ![]() находим
находим ![]() . То есть
. То есть ![]() значит треугольник
значит треугольник ![]() — равнобедренный. В равнобедренном треугольнике высоты, проведенные к основаниям равны (доказательство этого утверждения в статье «Задачи на доказательство геометрических фактов из ГИА»). Значит
— равнобедренный. В равнобедренном треугольнике высоты, проведенные к основаниям равны (доказательство этого утверждения в статье «Задачи на доказательство геометрических фактов из ГИА»). Значит ![]() . Тогда в прямоугольном треугольнике
. Тогда в прямоугольном треугольнике ![]() катеты
катеты ![]() и
и ![]() по
по ![]() , и он является равнобедренным. Значит искомый угол
, и он является равнобедренным. Значит искомый угол ![]() , так как это острый угол при основании равнобедренного прямоугольного треугольника.
, так как это острый угол при основании равнобедренного прямоугольного треугольника.
![Rendered by QuickLaTeX.com \[ \begin{cases} -11x +3\cdot\operatorname{ln} 17+\log_x(\log_2 x+\log_4 x + \\ +1) \geqslant \frac{1}{\log_2 x}-11x+3\cdot\operatorname{ln} 17, \\ 10x-14\cdot \operatorname{ln} 17+3^x+3^{x+1}>4^x+ \\ +10x-14\cdot \operatorname{ln} 17.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f6e30a2257c367a1b18db522eb7dfcc0_l3.png)
Решение задачи C3. Исходная система эквивалента следующей:
![Rendered by QuickLaTeX.com \[ \begin{cases} \log_x(\log_2 x+\log_4 x+1)\geqslant \frac{1}{\log_2 x}, \\ 3^x+3^{x+1}>4^x. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-a4e39638ead6d4c561cd005c01675fb7_l3.png)
1. Решаем сперва второе неравенство системы:
![]()
![]()
2. Решаем теперь первое неравенство. Область его допустимых значений определяется следующей системой:
![Rendered by QuickLaTeX.com \[ \begin{cases}x>0, \\ x\ne 1,\\ \log_2 x+\log_4 x+1>0\end{cases}\Leftrightarrow \begin{cases}x>0, \\ x\ne 1,\\ \log_2 x>-\frac{2}{3}\end{cases}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e8fbfa5f133b507bb9ef4102e06ea60c_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}x>0, \\ x\ne 1,\\ x>\frac{1}{\sqrt[3]{4}}\end{cases}\Leftrightarrow\begin{cases} x>\frac{1}{\sqrt[3]{4}}, \\ x\ne 1. \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-246a4dddf4e56550279d33e0e1f53c24_l3.png)
В области допустимых значений переходим к следующему равносильному неравенству:
![]()
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\begin{cases}x>1, \\ \frac{3}{2}\log_2 x + 1\geqslant 2\end{cases} \\ \begin{cases} 0<x<1, \\ \frac{3}{2}\log_2 x+1\leqslant 2 \end{cases} \end{array}\right.\Leftrightarrow \left[\begin{array}{l}\begin{cases}x>1, \\ \log_2 x \geqslant \frac{2}{3}\end{cases} \\ \begin{cases} 0<x<1, \\ \log_2 x \leqslant \frac{2}{3} \end{cases} \end{array}\right. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-11bb9ce93e3087834c3c666e9c5bca71_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l} \begin{cases}x>1, \\ x\geqslant \sqrt[3]{4}\end{cases} \\ \begin{cases} 0<x<1, \\ x\leqslant \sqrt[3]{4} \end{cases}\end{array}\right.\Leftrightarrow x\in(0;1)\cup(\sqrt[3]{4};+\mathcal{1}). \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-064c816bdf4df02f77f2a4493063c511_l3.png)
С учетом области допустимых значений: ![]()
С учетом, что ![]() комбинируя полученные в пунктах один и два ответы, находим окончательно:
комбинируя полученные в пунктах один и два ответы, находим окончательно:
![]()
Решение задачи C4.
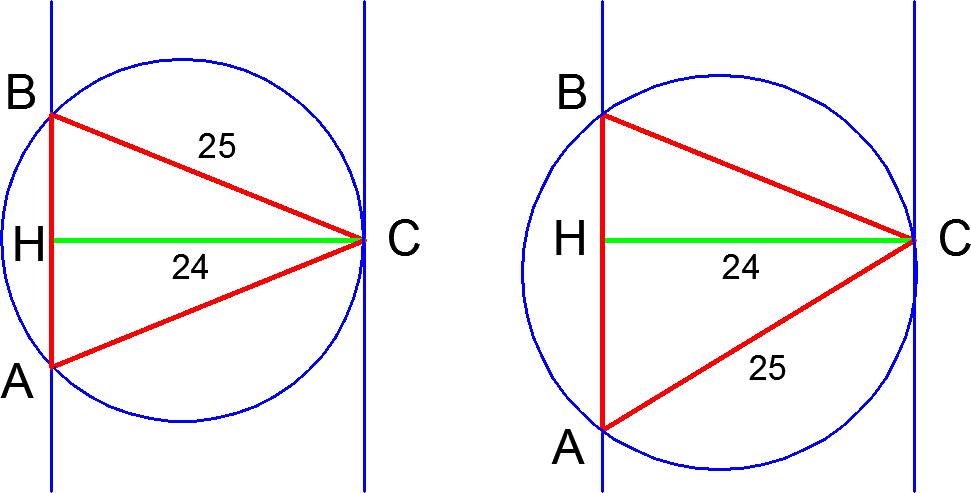
Возможны два случая (см. рисунок). Рассмотрим отдельно каждый.
1. В равнобедренном треугольнике ![]() основанием служит сторона
основанием служит сторона ![]() В этом случае
В этом случае ![]() , то есть
, то есть ![]() . Площадь треугольника в таком случае равна
. Площадь треугольника в таком случае равна ![]() . Тогда радиус описанной окружности можно вычислить по формуле:
. Тогда радиус описанной окружности можно вычислить по формуле: ![]()
2. В равнобедренном треугольнике ![]() основанием является сторона
основанием является сторона ![]() . Тогда
. Тогда ![]() кроме этого
кроме этого ![]() тогда
тогда ![]() то есть
то есть ![]() Площадь треугольника в таком случае равна
Площадь треугольника в таком случае равна ![]() Тогда радиус описанной окружности равняется
Тогда радиус описанной окружности равняется ![]()
Решение задачи C5. Исходное уравнение эквивалентно следующей совокупности:
![]()
Выясним сразу при каких значениях ![]() возможны совпадения корней этих уравнений. Пусть
возможны совпадения корней этих уравнений. Пусть ![]() — решение и того, и другого уравнения совокупности. Тогда имеет место система:
— решение и того, и другого уравнения совокупности. Тогда имеет место система:
![Rendered by QuickLaTeX.com \[ \begin{cases} x_0^2-x_0+a-a^2 = 0,\\ x_0^2+x_0+a^2+a = 0.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-a44ac2519e89a403b74c83f8effc4311_l3.png)
Вычитанием из первого уравнения второго получаем: ![]() . Подставляя это в первое уравнение, получаем:
. Подставляя это в первое уравнение, получаем:
![]()
Прямой подстановкой проверяем, что при этих значениях ![]() исходное уравнение будет иметь три различных корня. Этот случай нам подходит. При всех остальных
исходное уравнение будет иметь три различных корня. Этот случай нам подходит. При всех остальных ![]() решения уравнений совокупности будут различны.
решения уравнений совокупности будут различны.
Дискриминант первого уравнения равняется ![]() Дискриминант второго уравнения равняется
Дискриминант второго уравнения равняется ![]() Совокупность будет иметь три решения, если первое уравнение будет иметь два решения (его дискриминант был положителен), а второе при этом будет иметь одно решение (дискриминант был равен нулю), или наоборот. То есть имеет место следующая смешанная система:
Совокупность будет иметь три решения, если первое уравнение будет иметь два решения (его дискриминант был положителен), а второе при этом будет иметь одно решение (дискриминант был равен нулю), или наоборот. То есть имеет место следующая смешанная система:
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\begin{cases} 1-4a+4a^2 = 0, \\ 1-4a-4a^2>0 \end{cases} \\ \begin{cases} 1-4a+4a^2>0, \\ 1-4a-4a^2 = 0 \end{cases}\end{array}\right.\Leftrightarrow \left[\begin{array}{l}\begin{cases} a = \frac{1}{2}, \\ 1-4a-4a^2>0 \end{cases} \\ \begin{cases} 1-4a+4a^2>0, \\ \left[\begin{array}{l}a = \frac{\sqrt{2}-1}{2}, \\ a = \frac{\sqrt{2}+1}{2}\end{array}\right.\end{cases}\end{array}\right.\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-5b5c58af2cf2a79c6f26f9704325c6ae_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}a = \frac{\sqrt{2}-1}{2}, \\ a = \frac{-\sqrt{2}-1}{2}.\end{array} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-1c1b096bc86c78925ae6cf8b23791f89_l3.png)
Окончательный ответ: ![]()
Определите:
- наименьшее количество членов такой последовательности;
- наибольшее количество членов такой последовательности.
Решение задачи C6.
1. Из двух членов такая последовательность состоять не может. Действительно, если предположить обратное и обозначить один из членов за ![]() , то второй член равен либо
, то второй член равен либо ![]() либо
либо ![]() . Тогда сумма членов такой последовательности равна либо
. Тогда сумма членов такой последовательности равна либо ![]() либо
либо ![]() Ни в том, ни в другом случае натуральным
Ни в том, ни в другом случае натуральным ![]() не получается.
не получается.
А вот три члена в такой последовательности быть может: ![]() откуда получаем
откуда получаем ![]() а сама последовательность такова:
а сама последовательность такова: ![]() . Итак, минимальное количество членов такой последовательности равно
. Итак, минимальное количество членов такой последовательности равно ![]()
2. Если составлять последовательность из как можно большего числа членов, то каждый из них должен быть как можно меньше. Проанализировав некоторые возможные варианты, получаем, что данная последовательность должна быть следующего вида:
![]()
Ее сумма равняется ![]() а количество членов равно
а количество членов равно ![]() Итак, наибольшее количество членов данной последовательности равно
Итак, наибольшее количество членов данной последовательности равно ![]()
На этом все. Мои поздравления, если вы смогли добраться до конца, это уже маленькая победа. Задавайте свои вопросы в комментариях, учите математику и не только, подписывайтесь на обновления. Желаю вам блестящих результатов на экзаменах!
Репетитор по математике в Москве
Сергей Валерьевич
© Ари де Гиус


Спасибо Вам большое Вы мне очень-очень помогли!!!
You’re welcome. Рад помочь, обращайтесь:-)
Спасибо Вам большое) Очень помогло)))
Здравствуйте. Подскажите пожалуйста в задании С4 в первом варианте реешения как так у вас АВ=14? когда судя по расчётам из данных задачи и формуле расчёта АВ , сторона АВ = 69,3 …
Рисунок поменял, а текст старый остался, сейчас все опечатки убраны.