Задача о трёх черепахах

В этой статье репетитор по физике и математике рассказывает о том, как решить классическую олимпиадную задачу по физике о трёх черепахах, находящихся в вершинах равностороннего треугольника и движущихся с некоторой скоростью по направленю друг к другу. В статье присутствует ссылка на подробный видеоразбор задачи.

Когда я готовился к этому занятию, в Интернете я наткнулся вот на такую формулировку этой задачи.

По прямой дороге одна за другой ползут три черепахи. Одна из них говорит: «За мной ползут две черепахи». Другая отвечает: «Передо мной ползёт одна черепаха, и за мной ползёт одна черепаха». А третья при этом говорит: «За мной ползёт одна черепаха, а передо мной ползут две черепахи». Как такое возможно?

Я долго думал, как такое возможно. Ничего не придумал и решил посмотреть ответ. Нажал на кнопку, а там написано: «Третья черепаха лжёт». Вот так вот! Неожиданно, не правда ли?

Ну это ладно. Мы с вами будем решать, конечно же, не эту задачу. А гораздо более интересную. Формулируется она следующим образом.

Формулировка и решение задачи о трёх черепахах

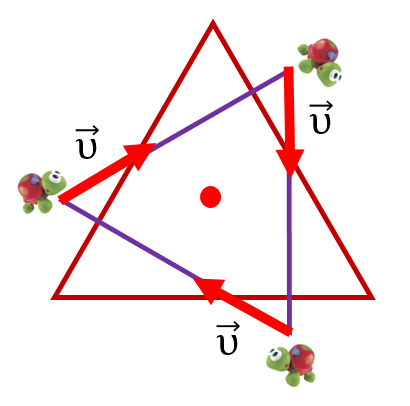
Есть три черепахи. Они находятся в вершинах равностороннего треугольника со стороной . И в какой-то момент времени все они начали двигаться с одинаковой скоростью, причём первая по направлению ко второй, вторая по направлению к третьей, а третья по направлению к первой, как показано на рисунке:

Причём эти направления всегда сохраняются во время движения. То есть в следующий момент времени, после того как каждая черепашка передвинулась на какое-то расстояние, она всё равно продолжает следовать по направлению к соседней черепашке. В результате наш треугольник поворачивается и уменьшается в размерах, но всё равно остаётся правильным, поскольку все черепашки одинаковые, и ситуация абсолютно симметричная.

Ну и понятно, что так будет продолжаться до тех пор, пока черепашки не встретятся, а произойдёт это, конечно же, в геометрическом центре исходного треугольника. Опять же в силу той же самой симметрии:

Вопрос в том, через какой промежуток времени произойдет эта встреча?

Можете попробовать решить задачу самостоятельно. Я уже рассказал большую часть решения. После того как решите, сравните мой ответ с тем, который получился у вас.

Итак, суть дела в том, что все черепашки одинаковы. Поэтому достаточно рассмотреть движение какой-то одной из них. Ну, например, верхней. Этой черепашке нужно добраться до  центра этого треугольника. Соединим центр треугольника и его вершину отрезком. Из геометрии мы знаем, что длина этого отрезка равна , где , напоминаю, длина стороны правильного треугольника.

Также известно, что величина каждого угла в правильном треугольнике равна . Ну тогда градусная мера половинки угла равна . Получается, что в процессе движения вектор скорости черепашки всегда будет направлен под углом к отрезку, соединяющему центр треугольника с его вершиной:

А это значит, что всегда постоянной будет оставаться и проекция скорости черепашки на этот отрезок. Чему равна эта проекция? Обозначим её . Она равна:

   

Для нахождения времени, которое потребуется черепашке, чтобы оказаться в центре треугольника, нужно разделить длину нашего отрезка на найденную проекцию скорости на этот отрезок. В результате получаем вот такое выражение:

   

Вот так вот решается эта олимпиадная задача. Мне, как репетитору по физике и математике, приходится готовить учеников и к олимпиадам тоже. Поэтому подобные задачи на занятиях я решаю с учениками довольно часто. Так что если вам требуется подготовиться к олимпиаде по физике или по математике, я могу помочь. На этом сайте вы сможете найти про меня всю необходимую информацию.

Решение задачи о трёх черепахах подготовил для вас репетитор по физике и математике в Москве, Сергей Валерьевич

Если вам понравилась эта статья, возможно, вам будут интересны следующие статьи:

• Задача на относительность движения о подводных лодках;
• Как найти косинус 36 градусов?