Геометрические задачи ЕГЭ с решениями

В данной статье разобраны решения геометрических задач, встречающихся в вариантах профильного ЕГЭ по математике. Всего таких задач 5: 3 из первой части и 2 из второй. По крайней мере, такой расклад был на момент написания статьи. Представленные материалы будут полезны тем, кто только начал подготовку к предстоящему экзамену. Здесь вы найдёте геометрические задачи ЕГЭ с решениями, снабжёнными подробными и понятными комментариями от профессионального репетитора по математике. Представлен также видеоразбор решений каждого задания.

Задачи представлены под номерами, под которыми они числятся в вариантах профильного ЕГЭ по математике.

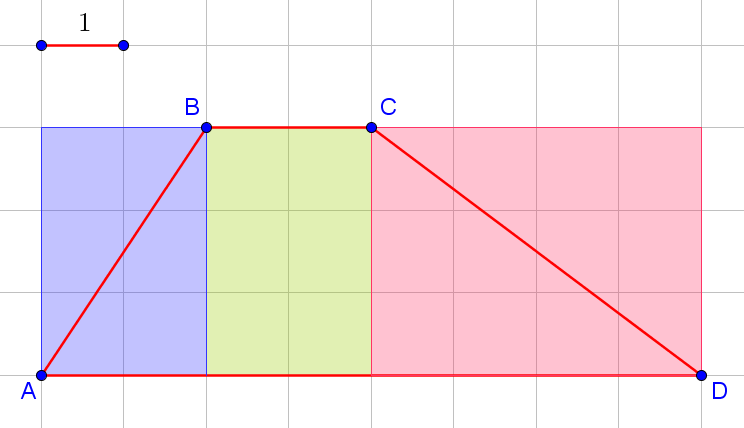
Задача 3. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.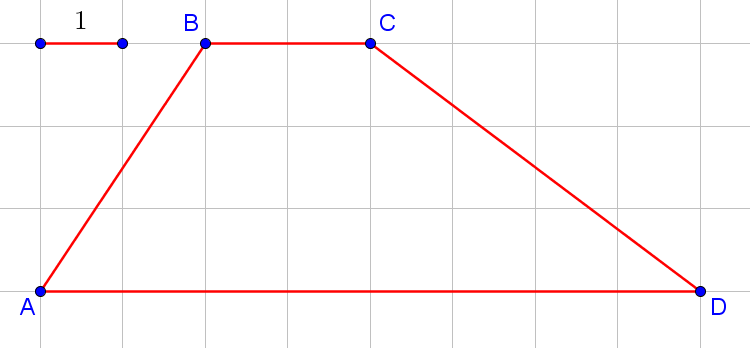

Даже если вы забыли формулу площадь трапеции на экзамене, не спешите отчаиваться. Вы всегда может решить задачу проще, чем вас научили в школе. В данном случае можно просто посчитать площадь по клеточкам:

Искомая площадь равна половине площади синего прямоугольника, плюс площади зелёного прямоугольника, плюс половина площади красного прямоугольника. Итого, получаем .

Задача 6. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.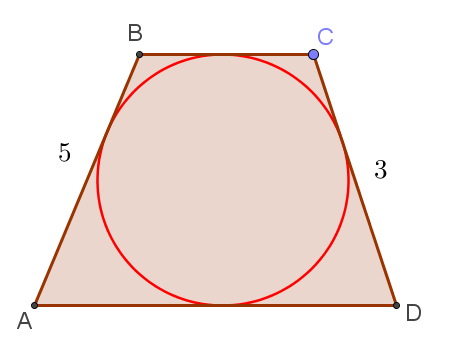

По-хорошему, рисунок здесь не нужен. Поскольку в трапецию вписана окружность, то суммы противоположных сторон равны. Следовательно, сумма оснований равна 8, а полусумма и, соответственно, средняя линия трапеции равны 4.

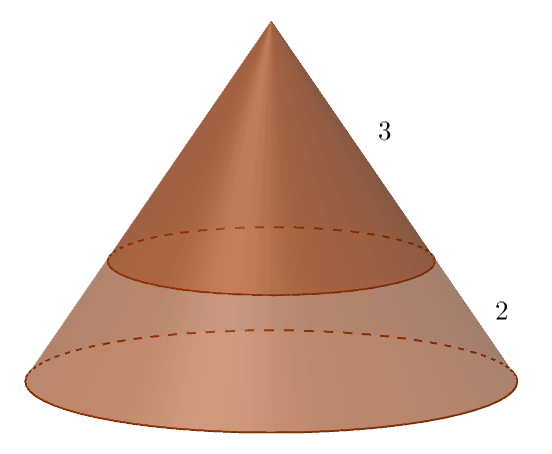
Задача 8. Площадь полной поверхности конуса равна 35. Сечение конуса плоскостью, проведенной параллельно основанию конуса, делит его высоту в отношении 3:2, если считать от вершины. Вычислите площадь полной поверхности полученного отсечённого конуса.

Все линейные размеры малого конуса в раз отличаются от линейных размеров большого конуса. Следовательно, квадратичные размеры (площадь поверхности) малого конуса в  раз отличаются от квадратичных размеров большого конуса. То есть искомая площадь полной поверхности отсечённого конуса равна .

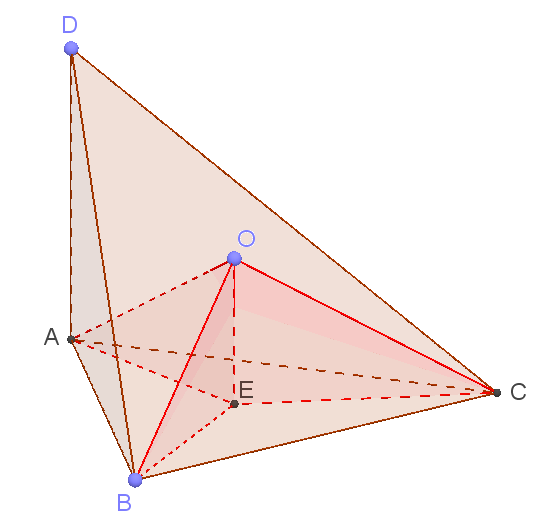
Задача 14. Дана пирамида ABCD такая, что в основании находится правильный треугольник ABC, а ребро AD перпендикулярно основанию. Все вершины пирамиды принадлежат сфере с центром в точке O. а) Докажите, что прямая, проходящая через точку O и центр описанной около треугольника ABC окружности, перпендикулярна плоскости ABC. б) Найдите радиус описанной сферы, если AB = 6, а AD = 4.

а) Из точки O опустим перпендикуляр OE на плоскость ABC:

Точка O равноудалена от точек A, B и C, так как O — центр описанной около пирамиды окружности. Тогда выделенные красным цветом прямоугольные треугольники AOE, BOE и COE равны по гипотенузе и катету.

Тогда AE = BE = CE. То есть точка E, лежащая в плоскости треугольника ABC, равноудалена от его вершин. Следовательно, она является центром описанной около него окружности. Что и требовалось доказать.

При доказательстве мы использовали так называемый метод решения с конца. Построили требуемый перпендикуляр и доказали, что данные условия задачи удовлетворены.

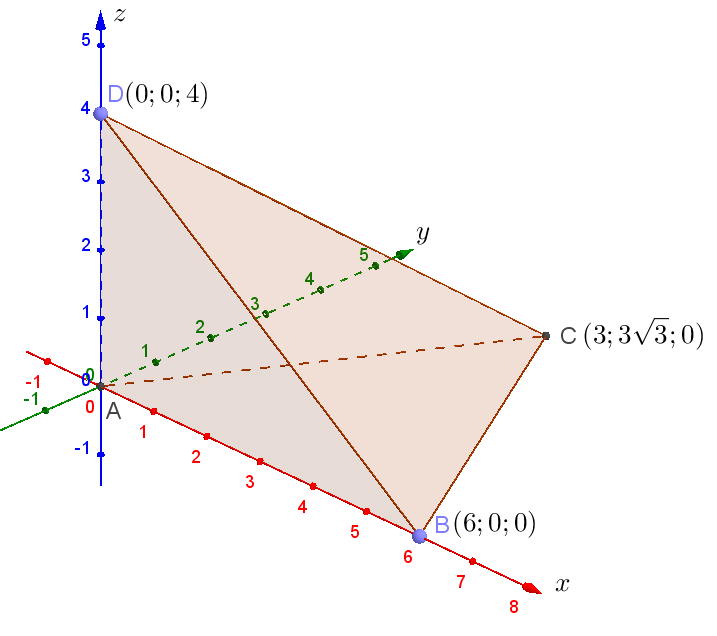
б) Введем систему координат, как показано на рисунке, и определим координаты вершин пирамиды в этой системе:

Пусть центр описанной около этой пирамиды сферы имеет координаты . Пусть радиус сферы равен . Тогда уравнение сферы во введённой системе координат имеет вид:

   

Этой сфере принадлежат все вершины данной пирамиды. Следовательно, имеет место следующая система:

   

Сравнивая первые два уравнения, получаем , откуда . Аналогично, сравнивая первое и третье уравнения, получаем , откуда .

Теперь подставляем полученные значения в первое и последнее уравнение. В результате приходим к системе:

   

Вычитаем почленно из первого уравнения второе и получаем:

   

Тогда из первого уравнения получаем, что , откуда . Отрицательное значение не берём, так как радиус не может быть отрицателен.

Обратите внимание, что попутно мы также получили координаты центра описанной сферы .

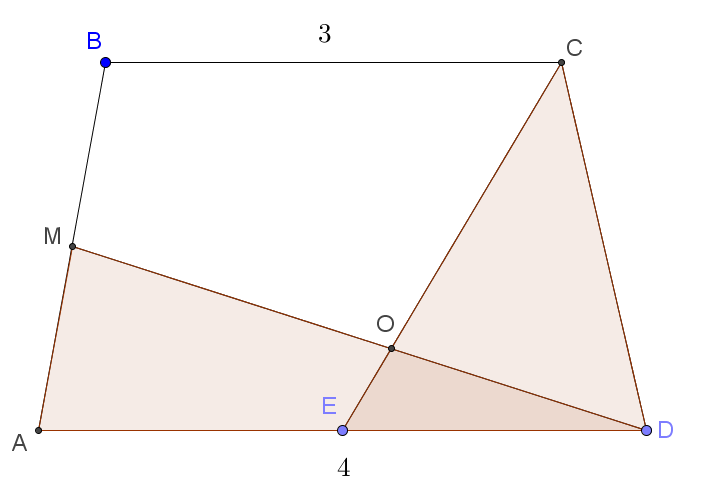
Задача 16. В трапеции ABCD точка E — середина основания AD, точка M — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O. a) Докажите, что площади четырёхугольника AMOE и треугольника COD равны. б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD = 4.

Изобразим чертёж к задаче:

а) Высота треугольника AMD из вершины M вдвое меньше высоты треугольника ECD из вершины C. При этом основание AD вдвое больше основания ED. Значит площади этих треугольников равны. А поскольку EOD — общая часть этих этих треугольников, то площади четырёхугольника AMOE и треугольника COD равны.

б) Обозначим высоту трапеции за . Тогда её площадь равна кв. ед., а площадь треугольника AMD равна кв. ед. Цель состоит в том, чтобы найти площадь треугольника EOD.

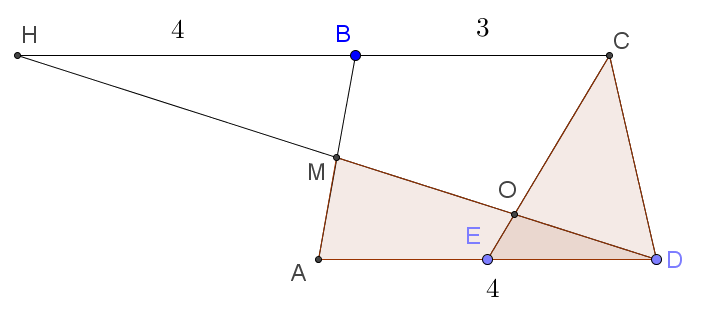
Выполним дополнительное построение: продолжим отрезок MD до пересечения с прямой BC в точке H. Тогда рисунок будет выглядеть следующим образом:

Треугольник HMB равен треугольнику AMD по стороне и двум прилежащим к ней углам. Следовательно, HB равно 4. Треугольник HCO подобен треугольнику ODE по двум углам. При этом коэффициент подобия равен .

Следовательно, высота треугольника OEA, проведенная к основанию ED, равна . Тогда площадь четырёхугольника AMOE равна кв. ед. Тогда искомое отношение равно .

Материал подготовлен репетитором по математике и физике в Москве, Сергеем Валерьевичем

Смотрите также:

• Задачи на доказательство геометрических фактов из ГИА;
• Разбор заданий первой части профильного ЕГЭ по математике;
• Разбор задачи 14 профильного ЕГЭ по математике.