Задание 14 из ЕГЭ по математике 2016

Суббота, 2 июля, 2016

В задании 14 ЕГЭ по математике выпускникам, сдающим экзамен, необходимо решить задачу по стереометрии. Именно поэтому научиться решать такие задачи должен каждый школьник, если он хочет получить положительную оценку на экзамене. В данной статье представлен разбор двух типов заданий 14 из ЕГЭ по математике 2016 года (профильный уровень) от репетитора по математике в Москве.

В правильной четырехугольной пирамиде SABCD сторона основания АВ равна 16, а высота равна 4. На ребрах АВ, CD и AS отмечены точки M, N и К соответственно, причем AM = DN = 4 и АК = 3.

а) Докажите, что плоскости MNK и SBC параллельны.

б) Найдите расстояние от точки К до плоскости SBC.

Доступен видеоразбор данного задания:

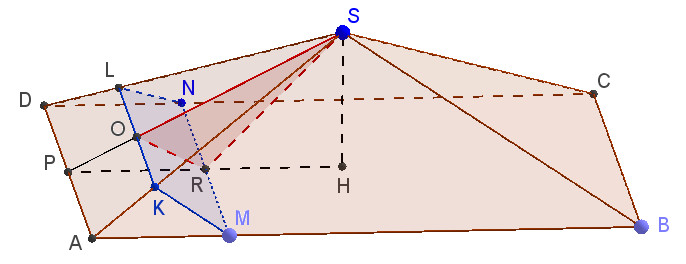
Рисунок к заданию будет выглядеть следующим образом:

а) Поскольку прямая MN параллельна прямой DA, которая принадлежит плоскости DAS, то прямая MN параллельна плоскости DAS. Следовательно, линия пересечения плоскости DAS и сечения KMN будет параллельна прямой MN. Пусть это линия KL. Тогда KMNL — искомое сечение.

Докажем, что плоскость сечения параллельна плоскости SBC. Прямая BC параллельна прямой MN, так как четырехугольник MNCB является прямоугольником (докажите сами). Теперь докажем подобие треугольников AKM и ASB. AC — диагональ квадрата. По теореме Пифагора для треугольника ADC находим:

$AC = \sqrt{AD^2+DC^2} = 16\sqrt{2}.$

AH — половина диагонали квадрата, поэтому $AH = 8\sqrt{2}$ . Тогда из теоремы Пифагора для прямоугольного треугольника $AHS$ находим:

$AS = \sqrt{AH^2+SH^2} = 12.$

Тогда имеют место соотношения:

$\frac{AK}{AS} = \frac{3}{12} = \frac{1}{4},\, \frac{AM}{AB} = \frac{4}{16} = \frac{1}{4}.$

Получается, что стороны, образующие угол A в треугольниках AKM и ASB, пропорциональны. Следовательно, треугольники подобны. Из этого следует равенство углов, в частности, равенство углов AMK и ABS. Так как эти углы соответственные при прямых KM, SB и секущей MB, то KM параллельна SB.

Итак, мы получили, что две пересекающиеся прямые одной плоскости (KM и NM) соответственно параллельны двум пересекающимся прямым другой плоскости (SB и BC). Следовательно, плоскости MNK и SBC параллельны.

б) Поскольку плоскости параллельны, расстояние от точки K до плоскости SBC равно расстоянию от точки S до плоскости KMN. Ищем это расстояние. Из точки S опускаем перпендикуляр SP к прямой DA. Плоскость SPH пересекается с плоскостью сечения по прямой OR. Искомое расстояние есть длин перпендикуляра из точки S к прямой OR.

Действительно, KL перпендикулярна плоскости OSR, так как она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости (OR и OS). Перпендикулярность OR и KL следует из теоремы о трёх перпендикулярах. Следовательно, KL перпендикулярна высоте треугольника ORS, проведенной к стороне OR. То есть эта высота перпендикулярна двум пересекающимся прямым, лежащим в плоскости KMN, а значит перпендикулярна этой плоскости.

Ищем стороны треугольника SOR. Сторону SR ищем по теореме Пифагора из прямоугольного треугольника RSH: $SR = 4\sqrt{2}$ . Длину SP находим по теореме Пифагора из прямоугольного треугольника PSH: $SP = 4\sqrt{5}$ . Треугольники SOK и SPA подобны (докажите это сами) с коэффициентом подобия $\frac{3}{4}$ . Тогда $SO = 3\sqrt{5}$ и $OP = \sqrt{5}$ . Из прямоугольного треугольника SPH находим $\cos\angle SPH = \frac{2}{\sqrt{5}}$ . Из теоремы косинусов для треугольника POR находим, что $OR = \sqrt{5}$ . Итак, нашли все стороны треугольника SOR.

Из теоремы косинусов для треугольника SOR находим $\cos\angle OSR = \frac{3}{\sqrt{10}}$ , тогда из основного тригонометрического тождества находим $\sin\angle OSR = \frac{1}{\sqrt{10}}$ . Тогда площадь треугольника OSR равна:

$S = \frac{1}{2}\cdot SO\cdot SR\sin\angle OSR =\frac{1}{2}\cdot 3\sqrt{5}\cdot 4\sqrt{2}\cdot\frac{1}{\sqrt{10}} = 6.$

С другой стороны эта площадь равна $S = \frac{1}{2}\sqrt{5}\cdot h$ , где h — искомая высота. Откуда находим $h = \frac{12}{\sqrt{5}}$ .

В правильной треугольной призме АВСА₁В₁С₁ сторона основания АВ равна 6, а боковое ребро АА₁ равно 3 . На ребре В₁С₁ отмечена точка L так, что B₁L = 1. Точки К и М – середины ребер АВ и А₁С₁ соответственно. Плоскость γ параллельна прямой АС и содержит точки К и L.

а) Докажите, что прямая ВМ перпендикулярна плоскости γ.

б) Найдите объем пирамиды, вершина которой – точка М, а основание – сечение данной призмы плоскостью γ.

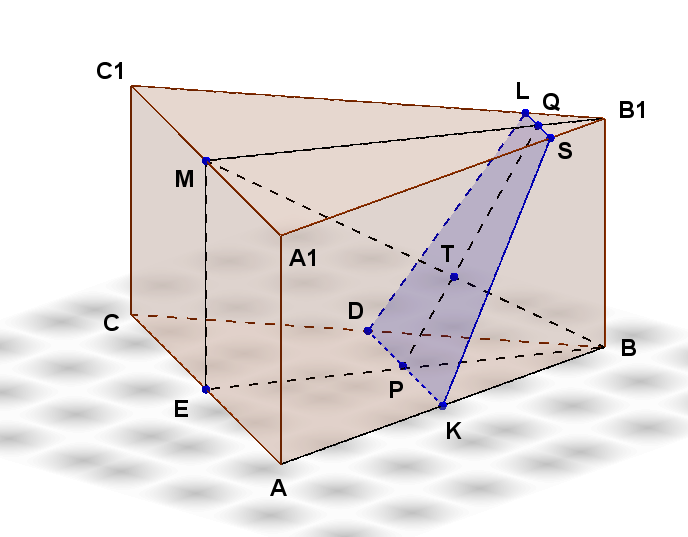
Плоскости оснований призмы параллельны, поэтому сечение будет пересекать эти плоскости по прямым LS и DK, которые также параллельны. Пусть B₁M — высота треугольника A₁B₁C₁, а BE — высота треугольника ABC. Тогда рисунок будет выглядеть следующим образом:

Из прямоугольного треугольника B₁MA₁ находим по теореме Пифагора $B_1M = 3\sqrt{3}$ . Из прямоугольного треугольника B₁QS находим по теореме Пифагора $B_1Q = \frac{\sqrt{3}}{2}$ . Тогда $MQ = B_1M - B_1Q = \frac{5\sqrt{3}}{2}$ . Кроме того $PB = \frac{3\sqrt{3}}{2}$ (половина высоты BE правильного треугольника ABC). Треугольники MQT и PTB подобны по двум углам (углы PTB и MTQ равны как вертикальные, углы TPB и MQT равны как накрест лежащие при параллельных прямых MQ, PB и секущей PQ). Их коэффициент подобия равен $k = \frac{MQ}{PB} = \frac{5}{3}$ .

Далее из прямоугольного треугольника MBE находим $MB = \sqrt{BE^2+ME^2} = 6$ . Используя доказанное подобие, находим $TB = \frac{MB}{1+k} = \frac{9}{4}$ . Аналогично, $PQ = 2\sqrt{3}$ . Следовательно, $TP = \frac{2\sqrt{3}}{1+k} = \frac{3\sqrt{3}}{4}$ .

Проверяем, является ли треугольник TPB прямоугольным. Для этого используем теорему, обратную теореме Пифагора. $TP^2 = \frac{27}{16}$ , $TB^2 = \frac{81}{16}$ , $BP^2 = \frac{27}{4}$ . Получаем:

$TP^2 + TB^2 = \frac{27}{16}+\frac{81}{16} = \frac{27}{4} = BP^2.$

Итак, треугольник TPB прямоугольный с прямым углом T. Доказано, что $MB\perp PQ$ . По теореме о трёх перпендикулярах $MB\perp DK$ (разберитесь самостоятельно, почему это так). Получается, что MB перпендикулярен двум пересекающимся прямым, лежащим в плоскости DKS, а следовательно перпендикулярен этой плоскости.