Задачи на применение теоремы Пифагора

Когда вы только начинали изучать квадратные корни и способы решения иррациональных уравнений (равенств, содержащих неизвестную под знаком корня), вы, вероятно, получили первое представление об их практическом использовании. Умение извлекать квадратный корень из чисел также необходимо для решения задач на применение теоремы Пифагора. Эта теорема связывает длины сторон любого прямоугольного треугольника.

Пусть длины катетов прямоугольного треугольника (тех двух сторон, которые сходятся под прямым углом) будут обозначены буквами  и , а длина гипотенузы (самой длинной стороны треугольника, расположенной напротив прямого угла) будет обозначена буквой . Тогда соответствующие длины связаны следующим соотношением:

(сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины его гипотенузы).

Данное уравнение позволяет найти длину стороны прямоугольного треугольника в том случае, когда известна длина двух других его сторон. Кроме того, оно позволяет определить, является ли рассматриваемый треугольник прямоугольным, при условии, что длины всех трёх сторон заранее известны.

Решение задач с использованием теоремы Пифагора

Для закрепления материала решим следующие задачи на применение теоремы Пифагора.

Задача 1. Используя приведённые ниже данные о длинах сторон прямоугольных треугольников, вычислите длины других сторон.

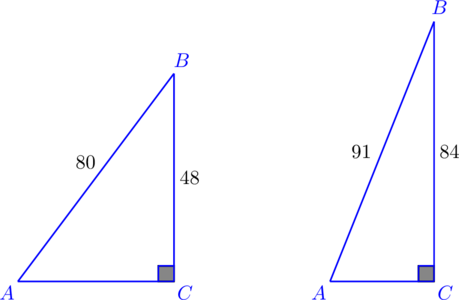
Итак, дано:

1. Длина одного из катетов равняется 48, гипотенузы – 80.
2. Длина катета равняется 84, гипотенузы – 91.

Приступим к решению:

a) Подстановка данных в приведённое выше уравнение даёт следующие результаты:

48²+ b² = 80²

2304 + b² = 6400

b² = 4096

b = 64 или b = -64

Поскольку длина стороны треугольника не может быть выражена отрицательным числом, второй вариант автоматически отбрасывается.

Ответ к первому рисунку: b = 64.

b) Длина катета второго треугольника находится тем же способом:

84²+ b² = 91²

7056 + b² = 8281

b² = 1225

b = 35 или b = -35

Как и в предыдущем случае, отрицательное решение отбрасывается.

Ответ ко второму рисунку: b = 35

Задача 2. Используя приведённые ниже данные о длинах сторон треугольников, определите, являются ли они прямоугольными.

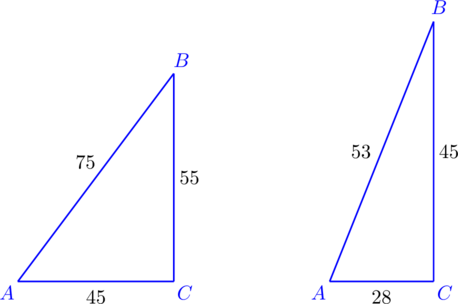
Нам дано:

1. Длины меньших сторон треугольника равны 45 и 55 соответственно, большей – 75.
2. Длины меньших сторон треугольника равны 28 и 45 соответственно, большей – 53.

Решаем задачу:

a) Необходимо проверить, равна ли сумма квадратов длин меньших сторон данного треугольника квадрату длины большей:

75²= 5625

45²+ 55² = 2025 + 3025 = 5050

5625 ≠ 5050

Следовательно, первый треугольник не является прямоугольным.

b) Выполняется та же самая операция:

53²= 2809

28²+ 45² = 784 + 2025 = 2809

2809 = 2809

Следовательно, второй треугольник является прямоугольным.

Задача 3. Даны точки (-2, -3), (2, 1), (5, -2) в прямоугольной системе координат на плоскости. Выясните, являются ли они вершинами прямоугольного треугольника.

Сперва найдем длину наибольшего отрезка, образованного точками с координатами (-2, -3) и (5, -2). Для этого используем известную формулу для нахождения расстояния между точками в прямоугольной системе координат:

   

Аналогично находим длину отрезка, заключенного между точками с координатами (-2, -3) и (2, 1):

   

Наконец, определяем длину отрезка между точками с координатами (2, 1) и (5, -2):

   

Поскольку имеет место равенство:

   

то соответствующий треугольник является прямоугольным.

Таким образом, можно сформулировать ответ к задаче: поскольку сумма квадратов сторон с наименьшей длиной равняется квадрату стороны с наибольшей длиной, точки являются вершинами прямоугольного треугольника.

Задача 4. Мальчик Ваня строит ворота. В высоту они должны достигать двух метров, в ширину – трёх. Если допустить, что углы, образованные косяками, окажутся прямыми, то какова будет длина троса, протянутой по диагонали от одного угла к другому?

Основание (расположенное строго горизонтально), косяк (расположенный строго вертикально) и трос (протянутый по диагонали) формируют прямоугольный треугольник, соответственно, для нахождения длины троса может использоваться теорема Пифагора:

   

Таким образом, длина троса будет составлять приблизительно 3,6 метра.

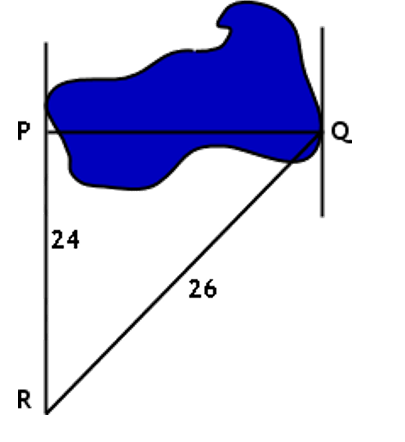
Задача 5. Мальчику Вите требуется измерить ширину пруда. Он нашёл расстояния от пункта R до пунктов P и Q, расположенных по разным сторонам пруда, как показано на рисунке ниже, и уверился в том, что угол P – прямой. Если допустить, что расчёты верны, какова протяжённость пруда с запада на восток?

Дано: расстояние от точки R до точки P (катет треугольника) равняется 24, от точки R до точки Q (гипотенуза) – 26.

Итак, помогаем Вите решить задачу. Поскольку стороны треугольника, изображённого на рисунке, предположительно образуют прямоугольный треугольник, для нахождения длины третьей стороны можно использовать теорему Пифагора:

   

Итак, ширина пруда составляет 10 метров.

Репетитор по математике на Юго-Западной, Сергей Валерьевич