В данной статье остановимся кратко на решении задач C1 из ЕГЭ по математике. Эти задания представляют собой уравнения, которые требуется, во-первых, решить (то есть найти их решения, причем все), во-вторых, осуществить отбор решений по тому или иному ограничению. В последние годы на ЕГЭ по математике в заданиях C1 школьникам предлагаются для решения тригонометрические уравнения, поэтому в данной статье разобраны только они. Примеры структурированы по методам решения уравнений, от самых элементарных, до достаточно сложных.
Прежде чем перейти к разбору конкретных тригонометрических уравнений, вспомним основные формулы тригонометрии. Приведем их здесь в справочном виде.
Решение простейших тригонометрических уравнений
![]()
принадлежащие промежутку ![]()
Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем ![]() (на всякий случай, эта запись означает, что числа
(на всякий случай, эта запись означает, что числа ![]() и
и ![]() принадлежат множеству целых чисел):
принадлежат множеству целых чисел):
![Rendered by QuickLaTeX.com \[ 4x+\frac{\pi}{4}=\pm\operatorname{arccos \left(-\frac{\sqrt{2}}{2}\right)}+2\pi k. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-600bd6daa90af5fa4124c683eb7663ac_l3.png)
Арккосинус ![]() есть число, заключенное в интервале от
есть число, заключенное в интервале от ![]() до
до ![]() , косинус которого равен
, косинус которого равен ![]() .
.
Арксинус ![]() есть число, заключенное в интервале от
есть число, заключенное в интервале от ![]() до
до ![]() , косинус которого равен
, косинус которого равен ![]() .
.
Другими словами, нам нужно подобрать такое число из промежутка ![]() косинус которого был бы равен
косинус которого был бы равен ![]() Это число
Это число ![]() Используя это, получаем:
Используя это, получаем:
![Rendered by QuickLaTeX.com \[ 4x+\frac{\pi}{4} = \pm\frac{3\pi}{4}+2\pi k\Leftrightarrow \left[\begin{array}{l}x = \frac{\pi}{8}+\frac{\pi k}{2}, \\ x = -\frac{\pi}{4}+\frac{\pi n}{2}.\end{array}\right. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4e1b7dcb8f1bb9b0ff44ee1900d0e206_l3.png)
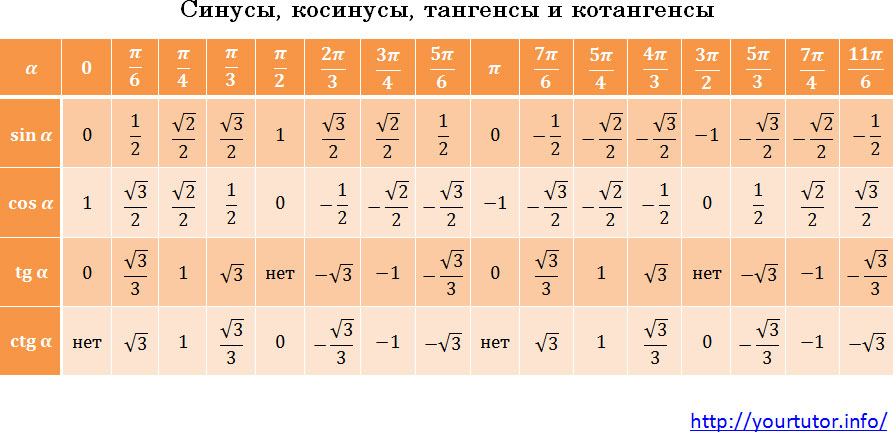
Вообще, значения тригонометрических функций от основных аргументов нужно знать. Их совсем чуть-чуть:
Хотя на самом деле запоминать их вовсе не обязательно. Существует очень простой алгоритм, используя который, можно в уме легко вычислять значения тригонометрических функций всех основных аргументов. Просто у каждого он свой. Придумайте его и для себя. Просто посмотрите на эту таблицу. Числа в ней расположены не случайным образом, определенная закономерность есть, постарайтесь ее найти.
Итак, вернемся к нашему заданию. Из полученных серий выбираем только те ответы, которые принадлежат промежутку ![]() Воспользуемся для этого методом двойных неравенств. Вы помните, что
Воспользуемся для этого методом двойных неравенств. Вы помните, что ![]() и
и ![]() — целые числа:
— целые числа:
1) ![]()
![]()
![]()
![]()
![]()
2) ![]()
![]()
![]()
![]()
![]()
Задача для самостоятельного решения №1. Найдите корни уравнения ![]() принадлежащие промежутку
принадлежащие промежутку ![]()
![]()
![]()
Решение линейных тригонометрических уравнений
![]()
принадлежащие промежутку ![]()
Решение. Подобные уравнения решаются один весьма интересным, на мой взгляд, способом. Разделим обе части на ![]() , уравнение тогда примет вид:
, уравнение тогда примет вид:
![]()
Подберем такое число, синус которого равен ![]() а косинус равен
а косинус равен ![]() Например, пусть это будет число
Например, пусть это будет число ![]() . С учетом этого перепишем уравнение в виде:
. С учетом этого перепишем уравнение в виде:
![]()
Присмотревшись, слева от знака равенства усматриваем разложение косинуса разности ![]() и
и ![]() Это и есть ключ к решению. Имеем:
Это и есть ключ к решению. Имеем:
![]()
![]()
Осуществляем отбор решений, входящих в промежуток ![]() :
:
1) ![]()
![]()
![]()
![]()
![]()
2) ![]()
![]()
![]()
![]()
![]()
Задача для самостоятельного решения №2. Найдите корни уравнения ![]() принадлежащие промежутку
принадлежащие промежутку ![]()
![]()
![]()
Решение тригонометрических уравнений методом замены переменной
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезке ![]()
Решение. Сразу оговорим ограничения, накладываемые на переменную ![]() в этом уравнении:
в этом уравнении: ![]() Откуда взялось это ограничение? Правильно, функция
Откуда взялось это ограничение? Правильно, функция ![]() не существует при этих значениях
не существует при этих значениях ![]() Используем замену переменной:
Используем замену переменной: ![]() Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
![]()
Переходим к обратной замене:
![]()
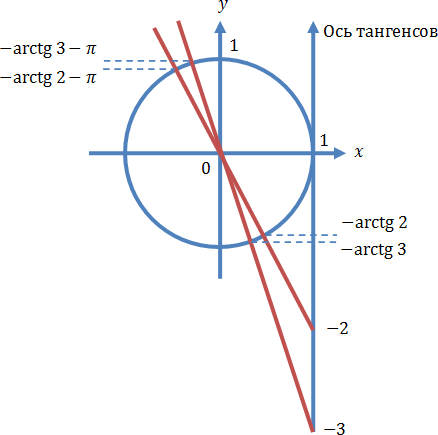
Осуществляем отбор решений. Проведем его на этот раз с использованием единичной окружности.
Из рисунка видно, что в интересующий нас промежуток входят только два значения из этих серий: ![]() Обратите внимание на один существенный момент. На рисунке точки
Обратите внимание на один существенный момент. На рисунке точки ![]() и
и ![]() принадлежат оси тангенсов, а точки
принадлежат оси тангенсов, а точки ![]()
![]()
![]() и
и ![]() — единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.
— единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.
Ответ: ![]()
Задача для самостоятельного решения №3. Дано уравнение ![]()
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![]()
![]()
![]()
Решение тригонометрических уравнений методом разложения на множители
![]()
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![]()
Решение. Равносильными преобразования приводим уравнение к виду:
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\cos x=1, \\ \sin x=-\frac{1}{2} \end{array}\right.\Leftrightarrow\left[\begin{array}{l}x=2\pi k, \\ x=-\frac{\pi}{6}+2\pi n, \\ x=-\frac{5\pi}{6}+2\pi z.\end{array}\right. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c0ac3379edc46ce1bf97df0f46a830ac_l3.png)
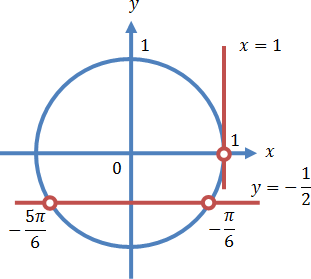
Осуществляем отбор решений с помощью единичной окружности.
Из рисунка видно, что в интересующий нас промежуток входят только два значения из всех этих серий: ![]()
Задача для самостоятельного решения №4. Дано уравнение
![]()
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![]()
![]()
![]()
Комбинированные уравнения
При решении уравнений этого типа важно обращать внимание на область допустимых значений входящих в него переменных. Именно поэтому составители вариантов ЕГЭ не просят учеников осуществлять отбор решений из полученных серий ответов. Решение этих уравнений само собой подразумевает выполнение данной математической операции.
![]()
Решение. Данное уравнение эквивалентно следующей системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}1-2\sin 3x\sin 7x=\cos 10x, \\ \cos 10x\geqslant 0.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-5e7804c5a3444eda3706d8c6a9cc8bc0_l3.png)
Обратите внимание! Писать, что ![]() нет никакой необходимости, поскольку по условию это выражение равно выражению
нет никакой необходимости, поскольку по условию это выражение равно выражению ![]() которое, в свою очередь, больше или равно нулю.
которое, в свою очередь, больше или равно нулю.
Решаем первое уравнение системы:
![]()
![]()
![]()
![]()
Нужно, чтобы ![]() поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только
поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только ![]()
Ответ: ![]()
Задача для самостоятельного решения №5. Решите уравнение: ![]()
![Rendered by QuickLaTeX.com \[ \frac{2\sin^2 x-\sin\left(\frac{3\pi}{2}+x\right)-1}{\sqrt{\sin x}}=0. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-b29f83ad79819cdf0623a3f50f53cbf1_l3.png)
Решение. Данное уравение равносильно системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}2\sin^2 x-\sin\left(\frac{3\pi}{2}+x\right)-1=0, \\ \sin x>0\end{cases}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-9796d3e88520ad252eea21fb51f21987_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}2\cos^2 x-\cos x-1=0,\\ \sin x>0\end{cases}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-dbab64445b6b27423f4c9a5b3a45e710_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}\left[\begin{array}{l}\cos x = 1, \\ \cos x =-\frac{1}{2},\end{array} \\ \sin x >0\right.\end{cases}\Leftrightarrow \begin{cases}\left[\begin{array}{l}x=2\pi k, \\ x=\pm\frac{2\pi}{3}+2\pi n,\end{array} \\ \sin x >0\right.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-20bc473770ab6419cd1a45ba72b7178f_l3.png)
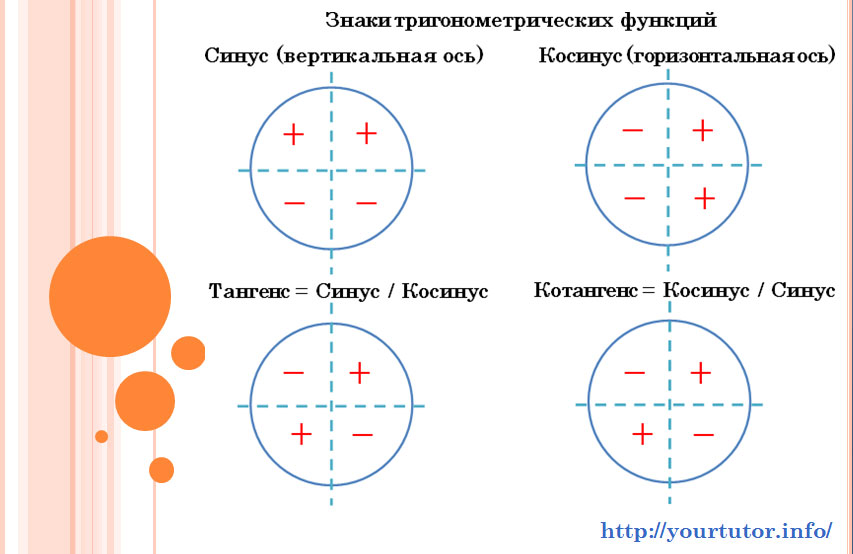
Тригонометрическая функция синус положительна в первой и второй координатной четвертях, поэтому из полученных серий выбираем только эту: ![]()
Раз уж мы с этим столкнулись, не лишним будет повторить, какие знаки принимают тригонометрические функций в различных координатных четвертях:
Ответ: ![]()
Задача для самостоятельного решения №6. Решите уравнение: ![]()
![]()
Решение. Область допустимых значения уравнения определяется условием: ![]() то есть
то есть ![]() Разобьем решение на два случая:
Разобьем решение на два случая:
1) Пусть ![]() тогда уравнение принимает вид:
тогда уравнение принимает вид:
![]()
![]()
Последнее равенство неверно, поэтому в данном случае решений у уравнения не будет.
2) Пусть ![]() тогда уравнение принимает вид:
тогда уравнение принимает вид:
![]()
![]()
Условию ![]() удовлетворяет только последняя серия.
удовлетворяет только последняя серия.
Ответ: ![]()
Задача для самостоятельного решения №7. Решите уравнение: ![]()
ЕГЭ по математике 2012 позади, все в ожидании результатов, которые обещали объявить во вторник 19 июня. Сейчас уже поздно желать высоких баллов на экзаменах нынешним выпускникам. Но вот пожелать успехов сегодняшним десятиклассникам я возможности не упущу. Удачи вам в подготовке и помните, что чем раньше она начнется, тем лучше будут результаты на экзамене.
Репетитор математики
Сергей Валерьевич
P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.





22sinx+23sin(2)x+23cos(2)x=22
Запись (2) означает «в квадрате»? Если да, то решение следующее: 23sin(2)x+23cos(2)x = 23 (основное тригонометрическое тождество). Тогда 22sinx+23=22, то есть sinx = -1/22, тогда x = (-1)^(n+1)*arcsin(1/22)+pi*n.
arctg(x+2)-arctg(x+3)=3П/4
Это уравнение корней не имеет. Поскольку y = arctg(x) — возрастающая функция, то выражение arctg(x+2)-arctg(x+3) всегда отрицательно и не может быть равно положительному числу 3П/4.
Добрый день, не могли бы вы подсказать , как решить уравнение 4cos(x/4+pi/6)=sqrt(3)
Делим обе части уравнения на 4, получаем: cos(x/4+pi/6)=sqrt(3)/4. Тогда x/4+pi/6 = +-arccos(sqrt(3)/4)+2pi*n, откуда x/4 = +-arccos(sqrt(3)/4)-pi/6+2pi*n, откуда x = +-4*arccos(sqrt(3)/4)-2pi/3+8pi*n.
помогите решить 14син 409* поделить на син49* пожалуйста ну очень надо!!!за ранние спасибо
Пожалуйста:
14sin(409*)/sin(49*) = 14sin(360*+49*)/sin(49*) = 14sin(49*)/sin(49*) = 14.
Обращайтесь.
128sin^2(20)sin^2(40)sin^2(60)sin^2(80)
9/2
Помогите решить,срочно надо:
1)2cos^2x+7sinx=5
2)sin(x+30 градусов)+cos(x+60 градусов)=1+cos2x
3)cosx*cos2x*cos4x*cos8x=1/16
Первое уравнение сводится к квадратичному относительно sin(x), дальше легко решается. Если воспользоваться основным тригонометрическим тождеством, то можно привести уравнение к виду: 2sin^2x-7sinx+3=0, решая которое получаем, что sinx=0.5, откуда x = (-1)^n*pi/6+pi*n.
Второе уравнение легко решить, воспользовавшись тем, что cos(x+60 градусов) = -sin(x-30 градусов). Доказать это можно с помощью формул приведения. Далее, используя формулу разности синусов, получаем 2sin(30 градусов)*cos(x)=1+cos2x. Далее, воспользовавшись формулой двойного косинуса, приводим уравнение к виду cosx-2cos^2x=0. Откуда cosx=0 или cosx = 0.5. Тогда ответ x = pi/2+pi*n или x =+-pi/3+2*pi*n.
Последнее умножением на sinx обеих частей решается. После всех преобразований (формула двойного синуса) получается, что sinx = sin16x. Дальше понятно. Переносишь в одну сторону и преобразуешь разность в произведение. Долго писать. Если еще актуально, или есть какие-нибудь вопросы — поясню подробнее.
Спасибо за полезную информацию. Всё четко. Отлично! В примере 3 верно указан промежуток? Может быть [-2П; -П/2].
Да, минус потерялся. Спасибо большое!
Нуждаюсь в помощи)
(2Sinx+√3)/(2Cosx+1)=0
Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю. Поэтому 2Sinx+√3=0, а 2Cosx+1 not= 0. Из первого получаем Sinx = -√3/2, откуда x = -П/3+2Пn или x = -2П/3+2Пn. Из второго получаем: Cosx not= -1/2, откуда x not= +-2П/3+2Пn. Значит из полученных при решении первого уравнения серий подходит только первая. Ответ: x = -П/3+2Пn.
Помогите, пожалуйста))
1)Sin4x/Cos4x-1=0
2)Cos(x/2-pi/12)(Sin(x-pi/3)+1)=0
3)(Cos4x+1)(Sin2x-1)=0
А в первом уравнении единица в знаменателе находится или из всей дроби вычитается?
При решении остальных используем то, что произведение равно нулю с том случае, если хотя бы один из множителей равен нулю. То есть приравниваем к нулю каждую из скобок и решаем полученные уравнения. Для первого: Cos(x/2-pi/12) = 0, откуда x/2-pi/12 = pi/2 + pi*n, откуда x = 7*pi/6+2*pi*n. Или Sin(x-pi/3)+1 = 0, откуда x-pi/3 = -pi/2 + 2*pi*n, откуда x = -pi/6 + 2*pi*n. Для второго: Cos4x+1 = 0, откуда 4x = -pi+2*pi*n, откуда x = -pi/4+pi/4*n. Или Sin2x-1 = 0, откуда 2x = pi/2+2*pi*n, откуда x = pi/4+pi*n.
спасибо большое))
Пожалуйста. Так а насчет первого то что? Или пропала уже необходимость?
первое я решила)
ctg^2x-(корень из 3-1) ctgx-корень из 3=0.. Надеюсь на помощь..
Замена: пусть ctgx = t. Уравнение t^2-(корень из 3-1) t-корень из 3=0 решается с помощью дискриминанта, получается два корня t=-1, t=корень из 3. Обратная замена: ctgx=-1, ctgx=корень из 3. Из первого получаем, что x=-pi/4+pi*n, из второго: x=pi/6+2pi*k, n,k — целые числа.
tg x= -1 Помогите
Почитайте выше, как такие уравнения решаются.
Ответ: x = -pi/4 + pi*n.
Уважаемый «репетитор» Сергей! Арккосинус a есть число, заключенное в интервале от 0 до 2\pi, косинус которого равен a.
Арксинус a есть число, заключенное в интервале от -\pi до \pi, косинус которого равен a.
. МОЖЕТ быть интервал все же о 0 до pi
Да, конечно, Вы правы.
sin^4(x)+cos^4(x)=7/8. заранее спасиба
Надо к обеим частям прибавить 2cos^2(x)*sin^2(x):
cos^4(x)+2cos^2(x)*sin^2(x)+sin^4(x)=7/8+2cos^2(x)*sin^2(x)
(cos^2(x)+sin^2(x))^2=7/8+0.5*sin^2(2x)
1=7/8+0.5*sin^2(2x)
sin^2(2x)=1/4
[sin(2x)=0.5
[sin(2x)=-0.5
[2x=(-1)^n*π/6+πn
[2x=(-1)^(n+1)*π/6+πn
[x=(-1)^n*π/12+πn/2
[x=(-1)^(n+1)*π/12+πn/2
или проще:
[x=-π/12+πn/2
[x=π/12+πn/2
Добрый день подскажите плиз синус пи на 6?????????????
Дмитрий, 1/2 (одна вторая).
Сергей, с Рождеством!
Уже продолжительное время не могу решить уравнение:2cosx-sinx=2+2sinx Перепробовала много подходов, но не получается.Что-то не учитываю. Помогите, пожалуйста.
Сергей,простите, допустила в условии ошибку:
2cosx-sin2x=2+2sinx
Наталья, спасибо. Вас тоже с Рождеством!
Вот решение:
sin2x+2sinx=2-2cosx. Перепишем в виде:
sin2x +1+ 2 (sin x + cos x) — 3=0
Замена: t = sinx+cosx.
Заметим, что t² = (sinx +cosx)² = sin ² x +2 sin x cos x +cos² x = 1+sin2x.
Тогда уравнение принимает вид:
t² +2t -3 =0.
Решения: t=1 и t= -3. Последний не подходит, поскольку sin x + cos x = -3
не имеет решений в силу ограниченности синуса и косинуса.
Тогда sin x + cos x =1. Используем формулу дополнительного аргумента: √2sin(x+π/4)=1. Откуда: x+π/4 = π/4+2πn и x+π/4 = 3π/4+2πn. Окончательно: х = π/2 +2πn и х = 2πn.
Сергей, огромное Вам СПАСИБО!!Я хорошо подумаю над этой методикой. Правда, одно решение в ответе отличается, но я все прорешаю( сейчас нет времени) и Вам сообщу.
Еще раз, спасибо, что Вы есть!
Сергей, добрый день! У Вас просто описка.
Когда Вы переносили из одной части ур-ния в другую, перепутали знак sin2x+2sinx=2cosx-2
{Хотя, эта манипуляция лишняя, все равно все переписывается слева.Тогда t=sinx-cosx , и корни t=-1 и t=3 Теперь еще вопрос: если сворачивать через синус доп арг ,ответ полностью совпадает, а если через косину.с, то у меня получается -pi/2, а в ответе 3pi/2 Конечно, ответ совпадает, учитывая период, но все же как правильнее записать?Заранее спасибо.
Наталья, любой из этих вариантов записи будет правильным.
cos^4x + sin^4x= sinx cosx
помогите пожалуйста
К обеим частям нужно прибавить 2sin²x*cos²x. Получается:
sin^4+cos^4=sinx*cosx
sin^4+2sin²x*cos²x+cos^4=sinx*cosx+2sin²xcos²x
(sin²x+cos²x)² = sin2x/2 + sin²2x/2
2=sin2x+sin²2x
sin²2x+sin2x-2=0
(sin2x+2)(sin2x-1)=0
sin2x=1
2x=pi/2 + 2pi*k
x=pi/4 + pi*k
Вопрос по первому Задача для самостоятельного решения №1. Арксинус (-1/2) это 7п/6 или 11п/6, но при этих значениях у меня не получаються корни (-3п/4, -п/4) Где ошибка? Уже сутки думаю……)
Наталья, арксинус (-1/2) = -п/6. Арксинус может принимать значения только из промежутка [-п/2;п/2].
Добрый день! Задача для самостоятельного решения №1. Как я понимаю, значение арксинуса(-1/2) это 7п/6, но при этом значении не получаються корни (-п/4,-3п/4) Подскажите где ошибка)
арксинус(-1/2)= -p/6
Нет, арксинус(-1/2) = 2pi/3
можно спросить а как вы научились всему этому как вы запомнили все эти формулы
Было бы странно, если бы я их не запомнил, учитывая, что занимаюсь этим всю жизнь почти:-).
В первом примере ошибка! k= -1 .0 .1 .2. k/2 забыли домножить неравенство
Тут, действительно, ошибка была, спасибо большое. Еще один корень из промежутка добавился, соответственно.
пример 3 неправельно пример записан 5tg x должно быть
Спасибо, исправил.
почему вы решаете математику в линейку ,а не в клеточку ?
Мне кажется, что так удобнее)
3sin2x+cos2x=2cos²x
Помогите решить.
Решила, но есть сомнения…ох давно это было
Здравствуйте, Анна
3sin2x+cos2x=2cos^2x
Сначала формула понижения степени:
3sin2x+cos2x=2*(1+cos2x)/2
3sin2x+cos2x=1+cos2x
3sin2x=1
sin2x=1/3
2x=(-1)^n*arcsin1/3+пи*n
x=1/2((-1)^n*arcsin1/3)+пи*n/2
Здравствуйте, извините,не могли бы вы помочь мне? 1. найти корни уравнения cos (3x — п/2) = 1/2, принадлежащие полуинтервалу (п; 3п/2]
2. 3arcctg (-корень из 3/3 )+1/2 arccos (корень из 2/2) у меня получилось 17п/8, правильно? Буду вам очень признательна!
Здравствуйте,
1. 3x — п/2 = п/3 + 2пn или 3x — п/2 = -п/3 + 2пn. Откуда x = 5п/18+2пn/3 или x = п/18+2пn/3. Значит полуинтервалу (п; 3п/2] принадлежит только одно значение из второй серии при n = 2, оно равно x = 25*pi/18.
2. 3*(2п/3)+1/2*п/4 = 17п/8. Правильно)
Спасибо вам огромное!!!!! теперь я точно к контрольной готова;-)
Всегда пожалуйста! Удачи вам на контрольной:-)
И не забывайте учить математику)
ЗДРАВСТВУЙТЕ,СЕРГЕЙ.
Помогите, пожалуйста..
y=x2*cosx
y’=
Здравствуйте, если имелось ввиду y=x^2*cosx, то y’ = 2x*cosx — x^2*sinx.
помогите пожалуйста решить
(кв.корень из 1-cos^2 (x))+6*cos(2x)=0
После преобразования получаем: 1/2*(1+11 cos(2 x)) = 0, откуда x = +-1/2*arccos(-1/11)+pi*n.
здравствуйте, подскажите пожалуйста, почему в уравнении 4sin^2x=tgx на промежутке от минус пи до нуля входят решения -11пи/12 и -7пи/12, не могу сообразить по числовой окружности как это
Здравствуйте, можно преобразовать к виду: sin(x)*(4*sin(x)-1/cos(x))= 0, откуда корни: pi*n, pi/12+pi*n, 5*pi/12+pi*n. Там какой промежуток? (-pi;0) или [-pi;0]? На промежутке от минус пи до нуля входят решения -11пи/12 и -7пи/12 потому что -11pi/12 больше -12pi/12 = -pi, но меньше 0, аналогично -7*pi/12. Эти значения получаются для вторых серий при n=-1. Вообще, если не понятно, как решать с помощью окружности, можно решить с помощью двойных неравенств. Если промежуток [-pi; 0], то ответ получается 0, -pi, -11pi/12, -7pi/12.
2sin(x/2+π/4)=√(1+8sin(x/3)cos^2(x/3))
Наберите в поисковике «иррациональные тригонометрические уравнения», найдете много аналогичных примеров.
помогите решить модульsinx+модульcosx=1,4
Начните с возведения в квадрат обеих частей уравнения. Тогда уравнение сведётся к одному модулю: |sin(2x)| = 0.96, которое легко решается.
А как решить не уравнение, а выражение 7sin^4a-7cos^4a+1, ecли cos2a=3:8?
7sin^4a-7cos^4a+1 = 1-7(cos^2a-sin^2a)+1 = 1-7cos2a = -13/8
Здравствуйте, Сергей! будет ли ошибкой, если ответом к уравнению sinx=-1/2 записать такие две серии корней: х=5π/6+2πk и х=11π/6+2πk
Или обязательно -π/6+2π5 и -5π/6 +2πK?
Будет ли при проверке экспертами экзаменационной работы принят первый вариант ответа?
Здравствуйте, первый ответ точно не будет принят, он не правильный, правильно будет: х=7π/6+2πk и х=11π/6+2πk. Это ответ эксперты должны принять.
Конечно я ошиблась! Спасибо!
Здравствуйте,помогите пожалуйста)
Найти все корни уравнения sin2x + 16cos²x = 4
на промежутке [п/4;3п/2]
Само уравнение я решила ,получилось х=arctg2+пn; x=-arctg3/2+пn ,найти на промежутках не могу…
Здравствуйте. Посмотрите пример 3 из статьи, там подробно рассказано, как осуществлять отбор решений в этом случае. Отбирать корни нужно с помощью единичной окружности.
cos(п/2+x) = корень из 3 разделить на 2
Посмотрите пример №1, там абсолютно аналогичное задание.
Здравствуйте! Помогите, пожалуйста, решить
cos(4)x+cos(4)(x-п/4)=1/4
cos^4(x)+cos^4(x-Pi/4)=1/4
Нужно воспользоваться формулой понижения степени, после чего привести выражение к виду: sin(2x)+cos(2x) + 1 = 0. Последнее уже легко решается.
Спасибо! Всё получилось!
Пожалуйста, Ольга, обращайтесь ещё:)
y=cosx/2+1
и что с этим делать надо?
http://yourtutor.info/wp-content/ql-cache/quicklatex.com-8780e32081992db3864252eb90f3d88f_l3.png
Я не очень поняла как это решается, ответы совершенно другие выходят
Какие у Вас получаются ответы?
Здравствуйте! Как решается эта задача из ЕГЭ за 10 класс?
Найдите, при каких значениях параметра «а» уравнение
(15sinx-a-5)(15sinx+2a-5)=0 имеет ровно 2 решения на промежутке [0;2пи).
Очевидное решение при а=0. А как находятся другие решения (-20; -5) и {0} и {10}? Особенно непонятно почему дан такой ответ для первого промежутка?
Здравствуйте. Вот несколько идей. Уравнение эквивалентно двум: sinx = (a+5)/15 и sinx = (5-2a)/15. Используем то, что -1<=sinx<=1. Тогда первое уравнение имеет корни при -20<=a<=10, а второе - при -5<=a<=10. Из этих значений "a" надо выбрать такие, при которых у обоих уравнений в совокупности будет 2 не совпадающих корня.
система уравнений
cos 2x=1/2
sin 3x=-1
принадлежит промежутку (-п;п)
нужно найти количество решений
Решением второго уравнения является серия x = pi/2+2*pi*n/3. В промежуток (-pi;pi) из этой серии входят числа -5*pi/6, -pi/6, pi/6, 5*pi/6. Решением первого уравнения является серия x = +-pi/6 + pi*n. В промежуток (-pi;pi) входят числа -5*pi/6, -pi/6, pi/6, 5*pi/6. То есть общих решений 2 (-5*pi/6 и -pi/6).
здравствуйте. помогите, пожалуйста
2sin2(x/2 + X)=- кв.корень из 3 cosx
найти корни из [-3pi;-3/2pi]
Здравствуйте, sin2(x/2 + X) это синус в квадрате или 2 умножить на скобку?
Здравствуйте. Помогите, пожалуйста с уравнением.
2cosx+sinx+sin2x+1=0.
Здравствуйте.
Используем формулу двойного угла: sin2x = 2sinxcosx:
2cosx+sinx+2sinxcosx+1=0
sinx+1+2cosx(sinx+1)=0
(sinx+1)(1+2cosx) = 0
sinx+1=0 или 1+2cosx=0
sinx=-1 или cosx=-1/2
x=3pi/2+2pi*n или x=+-2pi/3+2pi*k
Последний пункт, я так понял ответ.
x=3π/2+2π умноженные на n? А во втором, умноженные на k? Верно?
Совершенно верно
Спасибо большое.
Здравствуйте ещё раз. У меня снова возникли трудности с уравнением. Помогите, если не трудно.
3√1+cosx (под корнем все от 1 до cosx)=√6 sinx.
Здравствуйте. При sin x>=0 при возведении обеих частей в квадрат получаем:
9(1+cosx) = 6sin^2x
3+3cosx = 2(1-cos^2x)
2cos^2x +3cosx+1 = 0
Замена: cosx = t
2t^2+3t+1 = 0
t = -1 или t = -1/2
Обратная замена:
cosx = -1 или cosx = -1/2
x = pi+2pi*n или x = +-2pi/3+2pi*k
Условию sinx>=0 удовлетворяют x = pi+2pi*n и x = 2pi/3+2pi*k.
Помогите, пожалуйста, с заданиями!
Вычислить:
1. tg x, если sin x = -12 / 13, х Є (pi; 3pi/2)
2. √3 tg x, если cos x = -4√3 / 7, х Є (pi / 2; pi)
И подскажите, что за тема и где её можно рассмотреть, чтобы самому разобраться. Заранее спасибо!
1. sin^2x+cos^2 = 1, откуда cosx = 5/13 и cosx = -5/13. Так как х Є (pi; 3pi/2), то подходит только cosx = -5/13. Тогда tgx = sinx/cosx = 12/5.
2. Здесь аналогично, sin x = 1/7 и sin x = -1/7. Так как х Є (pi / 2; pi), то подходит только sin x = -1/7. Тогда √3 tg x = 1/4.
Тема называется «Основные тригонометрические формулы». На мой взгляд, эта тема очень хорошо изложена в учебнике по математике Мордковича за 10 класс.