Решение «популярных» задач по физике на тему «Потенциал»

Разберем сегодня несколько задач по физике, связанных с вычислением потенциала сферы. Так уж сложилось, что новые задачи по физике появляются значительно реже, нежели, к примеру скажем, по математике. Оно и понятно, ведь придумать оригинальную физическую задачу далеко не просто. Из года в год в различных физических олимпиадах, вариантах ЕГЭ по физике и других диагностических работах появляются одни и те же задачи, причем зачастую авторы по разным причинам не меняют даже числовых значений входящих в условие параметров. Решение некоторых таких часто встречающихся (напрашивается назвать их «бородатыми», но мы назовем их лучше «популярными») задач приведено в данной статье.

Задача 1. В одну большую каплю сливают n одинаковых капелек ртути, заряженных до потенциала φ. Каков будет потенциал Φ этой капли? Считать, что капли имеют сферическую форму.

Решение. Потенциал заряженного шара (коим по условию является каждая из капель) определяется по формуле:

   

где Q — заряд шара, ε₀ = 8,85 · 10^-12 Ф/м — диэлектрическая постоянная, R — радиус шара.

Тогда потенциал образовавшейся после слияния капли можно определить так:

   

Общий заряд Q, по закону сохранения заряда, определяется суммой зарядов q каждой маленькой капли: Q = n · q. Как связать радиус R получившейся большой капли с радиусом r каждой малой? Используем то, что в результате слияния не изменяется объем ртути, то есть (предполагается, что вы помните формулу для вычисления объема шара, если нет — загляните сюда):

   

Итак, получаем:

   

Но

   

есть по определению потенциал одной маленькой капли, поэтому окончательно получаем ответ:

   

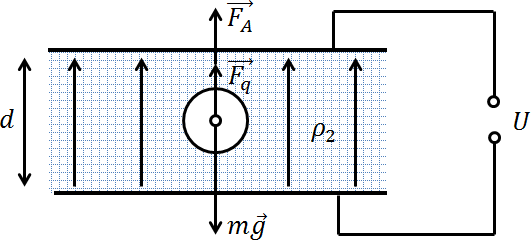
Задача 2. Металлический шар радиусом r помещен в жидкий диэлектрик с плотностью ρ₂. Плотность материала, из которого изготовлен шар, ρ₁ (ρ₁ > ρ₂). Чему равен заряд шара, если в однородном электрическом поле, направленном вертикально вверх, шар оказался взвешенным в жидкости? Электрическое поле создается двумя параллельными пластинами, расстояние между которыми d, а разность потенциалов U.

Решение.

На шар действуют три силы: сила тяжести mg = ρ₁gV (направлена вниз), выталкивающая сила Архимеда F_A = ρ₂gV (направлена вверх), сила Кулона F_q = qE (направлена вверх). То, что сила Кулона направлена вверх следует из того, что плотность материала шара больше плотности жидкого диэлектрика, в котором он плавает. Это означает, что он утонул бы, не будь он заряжен. Спасает его от этого дополнительная сила Кулона, сонаправленная с выталкивающей силой Архимеда.

Шар находится в равновесии, значит векторная сумма всех действующих на него сил равна нулю:

   

Или в проекции на вертикальную ось:

   

С учетом написанных выше формул:

   

С учетом формулы для объема шара (V = 4/3πr³) и формулы, отражающей взаимосвязь напряженности поля с напряжением между двумя точками (U=E·d), получаем окончательный ответ:

   

Задача 3. Проводник длиной l движется с постоянным ускорением a, направленным вдоль его оси. Определите напряжение, возникающее между концами проводника; m_e — масса электрона, |e| — элементарный заряд.

Решение. В процессе движения стержня часть электронов по инерции смещается к одному из его концов (ситуация напоминает поезд в метро — стержень — и едущих в нем пассажиров — электроны).

Процесс перетекания будет продолжаться до тех пор, пока возникшее в стержне электрическое поле не начнет действовать на электроны с силой |e|E, где E — напряженность этого поля, равной по величине m_ea. Напряженность поля связана с напряжением между концами проводника соотношением: U = E · l. После всех подстановок и преобразований получает ответ:

   

Задачи взяты из сборника В. И. Васюкова, С. Н. Дмитриева, Ю. А. Струкова «Физика: сборник задач для поступающих в вузы». Все задания в этом сборнике приведены с ответами, поэтому при желании вы можете самостоятельно оценить свои силы в их решении. Присылайте свои вопросы и интересные задачи, и мы обязательно разберем их в одной из следующих статей.

Репетитор по физике на Юго-Западной
Сергей Валерьевич