Пример устного вступительного экзамена в лицей «Вторая школа»

Автор

Понедельник, 15 мая, 2017

В данной статье представлен пример устного вступительного экзамена по математике в 9 класс лицея «Вторая школа», проходившего в 2017 году, с разбором всех заданий от профессионального репетитора, занимающегося подготовкой школьников к поступлению в этот лицей. Разбор варианта письменного вступительного экзамена во «Вторую школу» вы можете найти на этой странице.

Разбор заданий устного вступительного экзамена по математике в лицей «Вторая школа»


Всего на устном экзамене по математике в лицей «Вторая школа» в 2017 году абитуриентам было предложено 10 задач. Решение каждой задачи абитуриент должен был защитить перед экзаменатором. На защиту каждой задачи отводилось по 3 попытки. Если за первый час сдающий не смог защитить решение по крайней мере 3-х задач из первой пятёрки, экзамен считался не сданным. Ниже приведены цитаты формулировок заданий, предложенных в одном из вариантов, а также их подробное решение.

1. Соревновались 4 команды, каждая с каждой сыграла 1 раз. За победу давалось 3 очка, за ничью — 1 очко, за поражение — 0 очков. Команды набрали 5, 3, 3, 2 очка. Сколько было ничьих?

По результатам каждой игры в общую копилку очков добавлялось 3 очка (если одна команда победила другую) или 2 очка (если команды сыграли вничью). Всего было сыграно 6 матчей (1-я команда со 2-й, с 3-й, с 4-й; 2-ая команда с 3-й и с 4-й; 3-я команда с 4-й). Мы видим, что после всех игр в общей копилке оказалось 13 очков. Это нечётное число. Значит, была по крайней мере 1 победа, за которую какая-то команда получила 3 очка. Осталось 10 очков. Предположим, что они получились в общей копилке за 2-х побед и 2-х ничьих. Но тогда общее количество игр будет 5. Значит, единственно возможным вариантом остаётся, что эти 10 очков оказалось в общей копилке в результате 5-ти ничейных матчей. Других вариантов быть не может. То есть всего ничьих было 5.

Примечание. Результаты матчей были следующими: 1-я команда одержала победу в матче с 4-й, остальные 5 игр между командами прошли с ничейным результатом.

2. Чётное натуральное число n имеет 7 делителей, включая 1 и n. Сколько делителей имеет число 2n?

Представим чётное натуральное число n в каноническом разложении на простые сомножители:

    \[ n=2^{k_1+1}\cdot p_2^{k_2}\cdot p_3^{k_3}\dots p_n^{k_n}. \]

Здесь p_2,\, p_3,\, \dots ,\, p_n — простые числа, большие 2 и меньшие либо равные n, а k_1,\, k_2,\, \dots ,\, k_n — неотрицательные целые числа.

Тогда количество делителей числа n определяется по формуле:

    \[ N(n)=(k_1+2)(k_2+1)(k_3+1)\dots (k_n+1) = 7. \]

Первая скобка не может быть равна 1. Но поскольку 7 — простое число, то k_1+2=7 и k_1=5, а остальные скобки равны 1. То есть n = 2^6 = 64. Значит, 2n = 128 = 2^7. У этого числа 7+1=8 делителей.

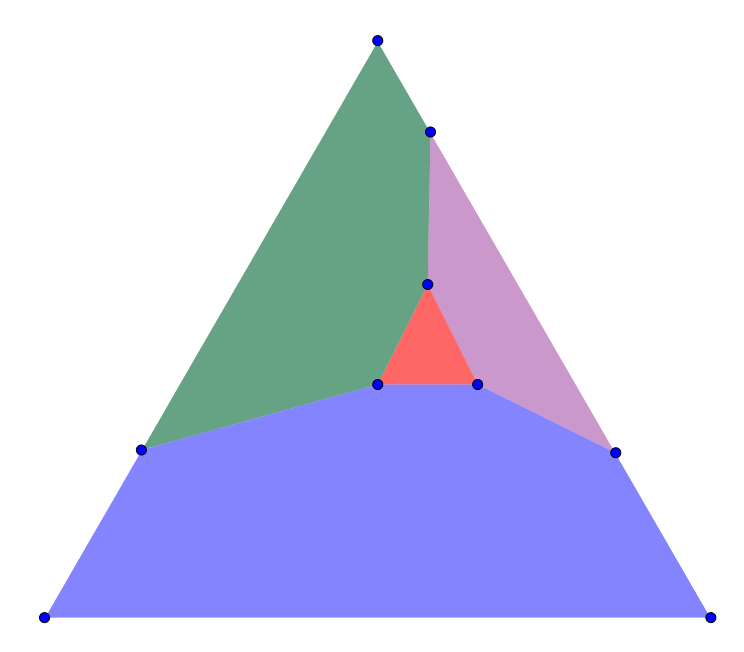
3. Разрежьте равносторонний треугольник на 4 выпуклые фигуры: шестиугольник, пятиугольник, четырёхугольник и треугольник.

Можно, например, разрезать его так:

Правильный треугольник, разрезанный на выпуклые многоугольники? треугольник, четырёхугольник, пятиугольник и шестиугольник

4. По кругу лицом в центр круга стоят мальчики и девочки, всего 20 детей (есть и те, и другие). У каждого мальчика справа стоит ребёнок в синей футболке, а у каждой девочки слева стоит ребёнок в красной футболке. Сколько в круге мальчиков?

Расположения типа МАЛЬЧИК — НЕИЗВЕСТНЫЙ РЕБЁНОК — ДЕВОЧКА невозможны, так как цвет футболки НЕИЗВЕСТНОГО РЕБЁНКА должен быть одновременно и красным, и синим. Значит, мальчики в круге должны стоять через одного, и их не меньше 10. По аналогичным соображениям девочек в круге тоже не меньше 10. Следовательно, и девочек, и мальчиков в круге по 10. Мальчики и девочки чередуются, все мальчики в красных футболках, все девочки в синих футболках.

5. Разместите в квадрате со стороной 1 несколько непересекающихся квадратов, так чтобы сумма их периметров была больше 2017. Квадраты могут иметь общую границу, но не могут иметь общих внутренних точек.

Пусть это будут одинаковые квадраты, каждый со стороной 0,001. Тогда периметр такого квадрата равен 0,004. Всего внутри исходного квадрата, согласно условиям задачи, можно разместить 1 000 000 таких квадратов. Сумма их периметров будет равна 4 000, что больше 2017.

6. В вершинах квадрата расставили натуральные числа a, b, c, d, а на сторонах написали произведения на концах. Сумма на рёбрах — 77. Найти сумму в вершинах.

Именно эту формулировку использовали авторы-составители. Стороны квадрата здесь обозвали «рёбрами». Но имелись ввиду именно стороны. Я это знаю точно, потому что мой ученик решал на экзамене эту задачу, исходя из того, что под рёбрами они понимали стороны квадрата. И эту задачу ему зачли. Ну и плюс к тому, по смыслу здесь больше ничего не подходит.

Итак, имеем, что ab + bc + cd + da = (a + c)(b + d) = 77. Так как у числа 77 только 4 натуральных делителя (1, 7, 11 и 77), то для натуральных чисел a, b, c, d возможно только, что a + c = 7 и b + d = 11 либо a + c = 11 и b + d = 7. В обоих случаях сумма в вершинах равна 18.

7. Есть 5 разных станков. Обучение одного рабочего на одном станке стоит N рублей. С какими наименьшими затратами можно обучить 8 рабочих так, чтобы при отсутствии любых трёх из них можно было использовать все 5 станков?

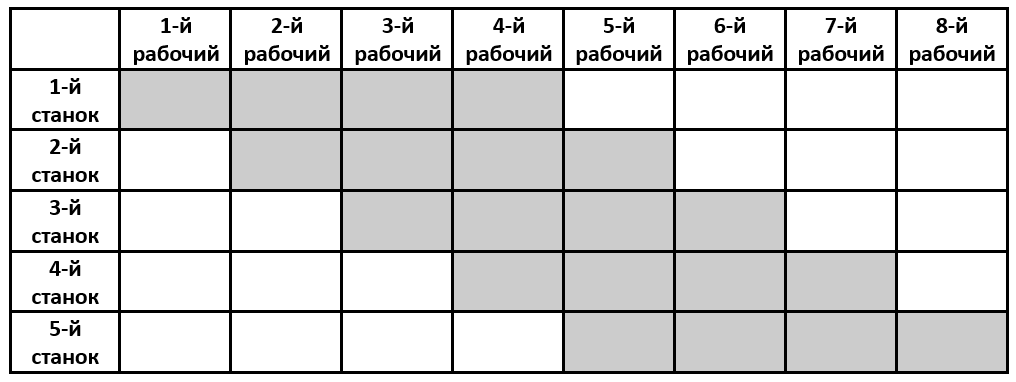
На каждом станке должны научиться работать как минимум по 4 рабочих. В противном случае возникает вероятность, что среди трёх отсутствующих рабочих окажутся все те, которые умеют работать на каком-то станке. То есть как минимум потребуется 5×4=20 циклов обучения, на которые будет потрачено 20N рублей. Приведём пример необходимого плана обучения рабочих. В приведённой ниже таблице строки соответствуют станкам, а столбцы — рабочим:

План обучения рабочих из задачи про станки из устного вступительного экзамена по математике в лицей "Вторая школа"

Как видно, при удалении любых трёх столбцов из этой таблицы среди рабочих останутся те, которые смогут работать на каждом из 5 станков.

8. Пусть M — точка внутри параллелограмма ABCD. Что больше: сумма расстояний от точки M до вершин параллелограмма или его периметр?

Эта задача — яркое демонстрация того, что только школьными знаниями при поступлении в лицей «Вторая школа» вам не обойтись. Вот смотрите, что вам понадобится для её решения. Во-первых, неравенство треугольника. Согласно этому неравенству длина любой стороны треугольника меньше суммы длин двух других сторон. Эту теорему ещё худо-бедно проходят на уроках в школе. Правда иногда уделяют этому настолько мало времени, что некоторые ученики, даже хорошие, просто проходят мимо этой теорема, вообще не понимая зачем она нужна. Но это отдельный вопрос. Главное проходят.

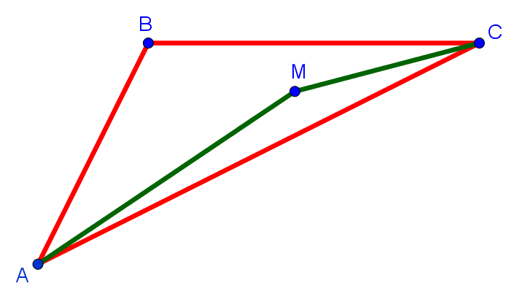
Вот собственно и всё, что дают в школе на эту тему на уроках геометрии в 7 классе. Но проблема в том, что очень малое количество школьников сможет решить эту задачу сходу, зная только теорему о неравенстве треугольника. И причина этого в том, что для решения этой задачи требуется знание ещё одного факта из геометрии, доказательство которого основано на неравенстве треугольника. И этот факт заключается в следующем. Если взять точку внутри треугольника, то сумма расстояний от этой точки до двух вершин треугольника, между которыми находится какая-то его сторона, меньше суммы двух других сторон этого треугольника. Чтобы стало понятно, изобразим это на рисунке:

Сумма расстояний от точки внутри треугольника до его вершин меньше суммы двух соседних сторон треугольника с концами в этих вершинах

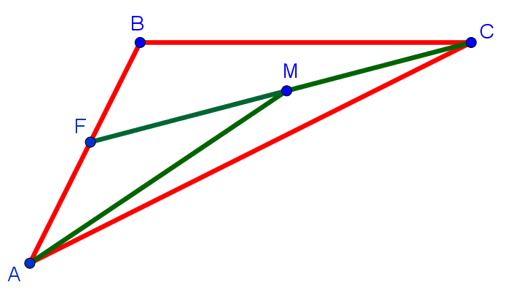
То есть на изображённом рисунке AM + MC < AB + BC. Казалось бы, что это очевидный факт. Но он не оформлен в школе как теорема, поэтому его обязательно нужно доказывать. Если вы его не докажите, то задача не будет решена. Вам за неё поставят 0 баллов. Как же нам доказать этот факт? Для этого продлим отрезок CM до пересечения со стороной AB в точке F:

Рисунок к доказательству того, что сумма расстояний от любой точки внутри треугольника до двух его вершин меньше суммы сторон этого треугольника, опирающихся на эти вершины

Применим теперь неравенство треугольника для треугольников FBC и AFM. Получим следующие неравенства: FC < BF + BC и AM < AF + FM. Сложим их почленно и представим FC как FM + MC. Получим следующее неравенство: FM + MC + AM < BF + BC + AF + FM. С учётом того, что BF + AF = AB. Получаем MC + AM < AB + BC, а это как раз то самое неравенство, которое нам нужно было доказать.

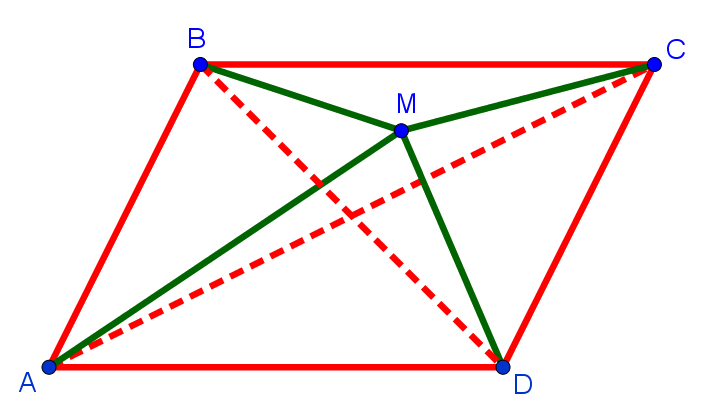
И только теперь, доказав эту лемму (теорему, необходимую для доказательства основной теоремы), мы готовы решить данную задачу. Изобразим ситуацию на рисунке:

Сумма расстояний от точки внутри параллелограмма до его вершин меньше периметра этого параллелограмма

Для треугольника ABC получаем AM + MC < AB + BC. Для треугольника BCD получаем BM + MC < BC + CD или, с учётом BC = AD (так как это противоположные стороны параллелограмма), BM + MC < AD + CD. Складываем почленно полученные неравенства и получаем: AM + MC + BM + MD < AB + BC + AD + CD. То есть сумма расстояний от точки внутри параллелограмма до его вершин меньше периметра этого параллелограмма.

Вот такое решение. Получается, что эту задачу можно решить, зная только неравенство треугольника, изучающееся в школьном курсе геометрии. То есть формально содержание задачи не выходит за рамки школьной программы. Но по факту очень мало кто из школьников может решить эту задачу. Даже из отличников, которые прекрасно знают, что такое неравенство треугольника. И это не из-за того, что они какие-то глупые или не обладают математическими способностями. Просто их в школе этому не научили. Ну а самостоятельно подготовиться в этом возрасте школьники не могут. Это нереально, да и времени всегда очень мало. Так что без дополнительной специальной подготовки не обойтись. И лучше всего, конечно, с профессиональным репетитором, который знаком со спецификой заданий из вступительных экзаменов.

9. Разложите 56 конфет по 14 пакетам так, чтобы с помощью этих пакетов можно было разделить конфеты поровну как между 7-ю, так и между 8-ю детьми. Перекладывать конфеты нельзя. В разных пакетах может быть одинаковое число конфет.

Нужно положить по 7 конфет в 7 пакетов, а в оставшиеся 7 пакетов положить по 1 конфете. Тогда, чтобы разделить конфеты поровну между 7-ю детьми, нужно каждому ребёнку выдать по 2 пакета: первый — с 7 конфетами, второй — с 1 конфетой. А для того, чтобы разделить конфеты поровну между 8-ю детьми, нужно 7 из них выдать по пакету с 7-ю конфетами, а оставшемуся ребёнку выдать оставшиеся 7 пакетов, в каждом из которых лежит по 1 конфете.

10. Числа 0<x_1<1,\, 0<x_2<1\dots 0<x_n<1 удовлетворяют соотношению

x_1x_2x_3\dots x_n = (1-x_1)(1-x_2)(1-x_3)\dots(1-x_n).

Найдите наибольшее возможное значение произведения

x_1x_2x_3\dots x_n.

Введём обозначение:

a=x_1x_2x_3\dots x_n = (1-x_1)(1-x_2)(1-x_3)\dots(1-x_n).

Тогда верно также следующее:

a^2=x_1(1-x_1)x_2(1-x_2)x_3(1-x_3)\dots x_n(1-x_n).

При этом из условия задачи следует, что 0<a<1. Из этого следует, что если a принимает наибольшее значение, то и a^2 также принимает наибольшее значение. Найдём это значение.

При любом i выражение x_i(1-x_i) принимает наибольшее значение \frac{1}{4} при x_i=\frac{1}{2}. Действительно, абсцисса вершины параболы y=x(1-x)=-x^2+x, ветви которой направлены вниз, находится в точке x_B=\frac{1}{2} (условие 0<x_B<1 соблюдено). Соответствующая ордината равна y_B=\frac{1}{4}. Это и есть наибольшее значение данной квадратичной функции. Наибольшее значение a^2 примет в том случае, если при любом i все произведения типа x_i(1-x_i) одновременно примут свои наибольшие значения \frac{1}{4}. Поскольку таких произведений n, то наибольшее значение a^2 равно \left(\frac{1}{4}\right)^n. Тогда наибольшее значение a равно \left(\frac{1}{2}\right)^n.

Вот такого уровня задания предлагаются на устном вступительном экзамене по математике в лицей «Вторая школа». И практика показывает, что очень часто школьники не могут решить те или иные задачи, не потому что они не способны к серьёзному изучению математики, а потому что они не знали к чему готовиться, что и как изучать, чтобы успешно сдать этот экзамен. Ну а школа не в состоянии дать необходимую подготовку, тем более если ученик учится в слабом классе. Так что специальная подготовка крайне необходима. И лучше всего — с профессиональным репетитором по математике и физике, который имеет большой опыт подготовки к вступительным экзаменам в лицей «Вторая школа» и знает, как в ограниченные сроки эффективно подготовиться к вступительному экзамену. И лучше всего начинать подготовку заранее. Чем раньше она начнётся, тем выше вероятность успеха.

Если вам была интересна эта статья, возможно вас заинтересую также следующие:

Метки: , , ,
Опубликовано в категории Методическая копилка | Нет комментариев »

Добавить комментарий