В данной статье представлен разбор варианта вступительного письменного экзамена по математике в лицей №2 (лицей «Вторая школа») для поступающих в 9 класс, который проходил в 2017 года. Стоит отметить, что сложность предлагаемых заданий оказалась в этом году в целом несколько выше, нежели в предыдущие годы. По-видимому, абитуриентов с каждым годом становится всё больше, а потому требования к знаниям потенциальных учеников лицея выдвигаются всё более высокие. Попробуйте решить эти задачи самостоятельно. Если у вас получится, то вы готовы к поступлению в этот лицей. Если нет — не расстраивайтесь. Всему можно научиться. Например, на занятиях с профессиональным репетитором для поступления в лицей «Вторая школа».
В данной статье представлен разбор варианта вступительного письменного экзамена по математике в лицей №2 (лицей «Вторая школа») для поступающих в 9 класс, который проходил в 2017 года. Стоит отметить, что сложность предлагаемых заданий оказалась в этом году в целом несколько выше, нежели в предыдущие годы. По-видимому, абитуриентов с каждым годом становится всё больше, а потому требования к знаниям потенциальных учеников лицея выдвигаются всё более высокие. Попробуйте решить эти задачи самостоятельно. Если у вас получится, то вы готовы к поступлению в этот лицей. Если нет — не расстраивайтесь. Всему можно научиться. Например, на занятиях с профессиональным репетитором для поступления в лицей «Вторая школа».
| 1. Найдите наименьшее общее кратное трёх чисел: 2235, 2334; 3253. |
Так как все числа уже разложены на простые сомножители, то для нахождения наименьшего общего кратного необходимо выбрать каждый из этих сомножителей в максимальной степени среди тех, что представлены в данных числах. В результате получится следующее число: 233553 = 243000.
| 2. Сократите дробь:
|
Используя стандартные правила умножения и деления степеней, а также возведения степени в степень, получаем следующий результат:
![Rendered by QuickLaTeX.com \[ \frac{\left(2^2\cdot 3x^2\right)^4}{\left(2^2\right)^2\left(3^2\cdot 2x^3\right)^3}=\frac{2^8\cdot 3^4\cdot x^8}{2^4\cdot 3^6\cdot 2^3\cdot x^9}=\frac{2}{9x}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ef3fc89574b2f32ca2a9e737265682c4_l3.png)
| 3. Разложите на два сомножителя: |
Используя известные формулы сокращённого умножения, можно преобразовать исходное выражение к требуемому виду следующим образом:
![]()
![]()
![]()
| 4. Дано |
Подобные задания часто встречаются в вариантах вступительных по математике в лицей лицей «Вторая школа». Для того, чтобы его решить, вынесем в числителе и знаменателе за скобки ![]() . В результате получаем:
. В результате получаем:
![Rendered by QuickLaTeX.com \[ \frac{b^2\left(\frac{a^2}{b^2}-1\right)}{b^2\left(\frac{a^2}{b^2}+1\right)} = \frac{\left(\frac{a}{b}\right)^2-1}{\left(\frac{a}{b}\right)^2+1} = \frac{\left(\frac{4}{3}\right)^2-1}{\left(\frac{4}{3}\right)^2+1} = \frac{7}{9}\cdot\frac{9}{25}=\frac{7}{25}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-a49cf6afd2a9dbdc36ed2ba4ecd3251e_l3.png)
| 5. Решите уравнение:
|
Конечно же вариант письменного экзамена по математике в лицей №2 не мог не содержать задания, в котором требуется решить уравнение. Для решения данного уравнения разложим правую часть на множители, используя формулу разность квадратов:
![]()
Применим эту формулу ещё раз для выражения, стоящего в первых скобках справа от знака равенства:
![]()
Перенесём всё в левую сторону равенства, изменив при этом знак на противоположный:
![]()
Теперь вынесем общие множители за скобки:
![]()
После упрощения получаем окончательно:
![]()
Произведение равно нулю, если хотя бы один из множителей равен нулю. То есть получаем три корня ![]() ,
, ![]() и
и ![]() .
.
| 6. Найдите все значения x и y, удовлетворяющие уравнению:
|
Данное уравнение содержит два неизвестных: ![]() и
и ![]() . Общего алгоритма для решения всех таких уравнений, к сожалению, не существует. Однако, иногда удаётся использовать какие-то частные приёмы, которые позволяют такие задания решать. Как репетитор по математике, на своих занятиях я как раз и занимаюсь тем, что обучаю своих учеников этим приёмам.
. Общего алгоритма для решения всех таких уравнений, к сожалению, не существует. Однако, иногда удаётся использовать какие-то частные приёмы, которые позволяют такие задания решать. Как репетитор по математике, на своих занятиях я как раз и занимаюсь тем, что обучаю своих учеников этим приёмам.
Вот что мы сделаем с данным уравнением. Перенесем все слагаемые в одну сторону и представим исходное уравнение в следующем виде:
![]()
Данное уравнение можно рассматривать как квадратное относительно переменной ![]() . Тогда соответствующие коэффициенты равны
. Тогда соответствующие коэффициенты равны ![]() ,
, ![]() и
и ![]() . Дискриминант такого уравнения равен:
. Дискриминант такого уравнения равен:
![]()
![]()
Если посмотреть на полученное выражение, то оно всегда неположительно. При всех отрицательных значениях у исходного уравнения корней не будет. Корень будет единственным при ![]() , то есть при
, то есть при ![]() . Из последнего уравнения получаем, что
. Из последнего уравнения получаем, что ![]() .
.
Теперь можно найти сам корень:
![]()
То есть получилась одна единственная пара чисел, удовлетворяющая этому уравнению: ![]() .
.
| 7. Плотность сплава 8 г/см3. Каков объём тонны сплава? |
Используем то, что 1 т = 1000 кг, 1 г = 10-3 кг, 1 см3 = 10-6 м3. Тогда плотность равна: 8 г/см3 = 8×10-3 кг/см3 = 8×10-3×106 = 8000 кг/м3. Тогда объём тонны сплава равен: 1000 (кг) / 8000 (кг/м3) = 0.125 м3.
| 8. Из 10 кг молока, содержащего 4% жира, сделали 1 кг сливок, содержащих 22% жира. Сколько процентов жира содержит оставшееся (обезжиренное) молоко? |
Содержание жира в 10 кг 4-процентного молока составляло 10×0,04 = 0,4 кг. Содержание жира в 1 кг 22-процентных сливок составляет 1×0,22 = 0,22 кг. Следовательно, из молока было изъято 0,18 кг жира. Поскольку масса полученных сливок составила 1 кг, то масса оставшегося обезжиренного молока равна 9 кг. Для ответа на вопрос осталось определить сколько процентов от 9 кг обезжиренного молока составляет 0,18 кг сливок: ![]() .
.
| 9. Решите уравнение:
|
Рассмотрим три случая:
1) При ![]() оба выражения, стоящие под знаком модуля, отрицательным. Поэтому в этом случае оба модуля нужно раскрывать со знаком минус. В результате получается следующее уравнение:
оба выражения, стоящие под знаком модуля, отрицательным. Поэтому в этом случае оба модуля нужно раскрывать со знаком минус. В результате получается следующее уравнение:
![]()
Однако этот корень не подходит, так как он не удовлетворяет условию ![]() .
.
2) При ![]() выражение
выражение ![]() положительно или равно нулю, а выражение
положительно или равно нулю, а выражение ![]() отрицательно или равно нулю. Поэтому первый модуль раскрывается со знаком плюс, а второй — со знаком минус. В результате получается следующее уравнение:
отрицательно или равно нулю. Поэтому первый модуль раскрывается со знаком плюс, а второй — со знаком минус. В результате получается следующее уравнение:
![]()
Как видно, полученное равенство верно при любом значении ![]() . Однако, мы берём только
. Однако, мы берём только ![]() .
.
3) При ![]() оба выражения, стоящие под знаком модуля, положительны. Поэтому оба модуля раскрываются со знаком плюс. В результате приходим к следующему выражению:
оба выражения, стоящие под знаком модуля, положительны. Поэтому оба модуля раскрываются со знаком плюс. В результате приходим к следующему выражению:
![]()
Однако этот корень не подходит, так как он не удовлетворяет условию ![]() .
.
Итак, окончательный ответ к заданию: ![]() .
.
Примечание. На самом деле этот ответ можно было бы получить, используя геометрический смысл модуля, который состоит в том, что выражение типа ![]() представляет собой длину отрезка числовой прямой между точками
представляет собой длину отрезка числовой прямой между точками ![]() и
и ![]() . Тогда задание можно переформулировать. Требуется найти такую точку
. Тогда задание можно переформулировать. Требуется найти такую точку ![]() на числовой прямой, сумма расстояний от которой до точек
на числовой прямой, сумма расстояний от которой до точек ![]() и
и ![]() равна
равна ![]() . Очевидно, что это любая точка между точками
. Очевидно, что это любая точка между точками ![]() и
и ![]() , а также сами эти точки.
, а также сами эти точки.
Однако, практика показывает, что такое решение понимается школьниками хуже, чем то, что приведено выше. Тем не менее, как репетитор для подготовки в лицей «Вторая школа» к вступительному по математике, на своих занятиях я предлагаю различные варианты решения задач. После этого в беседе с учеником мы определяем, какое решение для него является более простым и понятным.
| 10. Пешеход вышел из пункта A в 12.00 и пришел в пункт Б в 13.00. Велосипедист выехал из пункта A в 12.10 и приехал в пункт Б в 12.45. Сколько было времени, когда велосипедист обогнал пешехода? |
Пусть расстояние между пунктами A и B равно ![]() м, скорость пешехода равна
м, скорость пешехода равна ![]() м/мин, а скорость велосипедиста равна
м/мин, а скорость велосипедиста равна ![]() м/мин. Поскольку пешеход дошёл из пункта A в пункт B (прошёл расстояние
м/мин. Поскольку пешеход дошёл из пункта A в пункт B (прошёл расстояние ![]() ) за 1 час (60 минут), двигаясь со скоростью
) за 1 час (60 минут), двигаясь со скоростью ![]() м/мин, то имеет место равенство:
м/мин, то имеет место равенство: ![]() . Отсюда получаем, что
. Отсюда получаем, что ![]() Поскольку велосипедист преодолел расстояние из пункта A в пункт B (проехал расстояние
Поскольку велосипедист преодолел расстояние из пункта A в пункт B (проехал расстояние ![]() ) за 35 минут, двигаясь со скоростью
) за 35 минут, двигаясь со скоростью ![]() м/мин, то имеет место равенство:
м/мин, то имеет место равенство: ![]() . Отсюда получаем, что
. Отсюда получаем, что ![]() .
.
Через ![]() минут после начала движения пешехода, когда велосипедист его догнал, оба преодолели одинаковое расстояние. При этом велосипедист двигался на 10 минут меньше, чем пешеход, то есть
минут после начала движения пешехода, когда велосипедист его догнал, оба преодолели одинаковое расстояние. При этом велосипедист двигался на 10 минут меньше, чем пешеход, то есть ![]() минут. То есть имеет место равенство:
минут. То есть имеет место равенство: ![]() . С учётом полученных ранее формул получаем следующее уравнение:
. С учётом полученных ранее формул получаем следующее уравнение:
![]()
Используем правило пропорции (произведение крайних членов равно произведению средних). В результате получаем следующее выражение:
![]()
Итак, через 24 минуты после начала движения пешехода, велосипедист его догнал. На часах в этот момент было 12:24.
| 11. Запишите уравнение прямой, график которой проходит через точку А(100;45) и параллелен прямой y = 0,4x+50. |
За наклон прямой, как известно, отвечает коэффициент при переменной x. Поскольку искомая прямая параллельна прямой y = 0,4x+50, то её уравнение может быть записано в виде y = 0,4x+b. Осталось найти, чему равен коэффициент b. Поскольку искомая прямая проходит через точку A, то координаты этой точки должны удовлетворять уравнению этой прямой. Поэтому умеет место равенство:
![]()
Итак, искомое уравнение прямой имеет вид y = 0,4x+5.
| 12. Какие значения может принимать y, если |
Чтобы понять, как решается эта задача, нужно сперва понять, что за функция перед нами, и как выглядит её график. И на самом деле, если присмотреться, то можно увидеть, что перед нами типичная обратная пропорциональность. Графиком этой функции является гипербола, просто она смещена относительно нуля координат.
Чтобы это понять, поработаем с представленным выражением:
![]()
![]()
Вот теперь как раз видно, что график данной функции получается из графика функции ![]() путём его переноса на 3 единичных отрезка вверх и
путём его переноса на 3 единичных отрезка вверх и ![]() единичных отрезков вправо. У него будет горизонтальная асимптота
единичных отрезков вправо. У него будет горизонтальная асимптота ![]() и вертикальная асимптота
и вертикальная асимптота ![]() . Точка
. Точка ![]() по условию функции не принадлежит. Также по условию мы также должны исключить из этого графика точку с абсциссой 5. Ордината этой точки будет равна
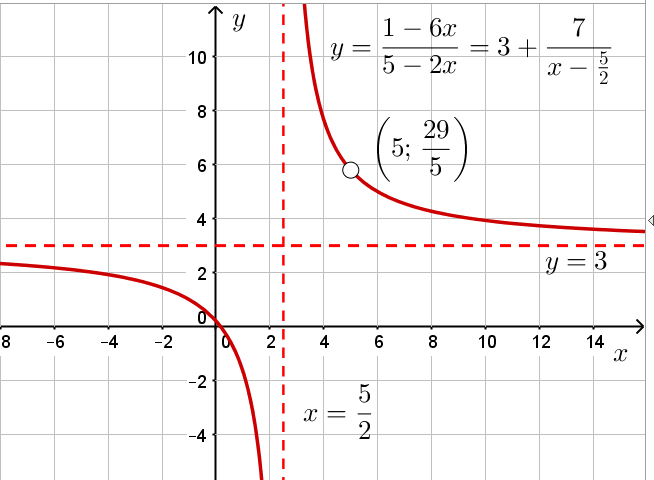
по условию функции не принадлежит. Также по условию мы также должны исключить из этого графика точку с абсциссой 5. Ордината этой точки будет равна ![]() . То есть вот как выгладит этот график:
. То есть вот как выгладит этот график:
Теперь видно, что область значений нашего исходного выражения задаётся следующим множеством:
![]() .
.
| 13. При каком значении x значение выражения |
Если рассмотреть квадратичную функцию ![]() , то её графиком будет парабола, ветви которой направлены вверх. При этом эта парабола пересекает ось OX в двух точках: x1=5,1 и x2=3,3. В силу симметрии параболы абсцисса её вершины находится ровно посередине между этими точками, то есть xв = (5,1+3,3)/2 = 4,2. Значение функции в этой точке будет являться наименьшим значением выражения (x — 5,1)(x — 3,3).
, то её графиком будет парабола, ветви которой направлены вверх. При этом эта парабола пересекает ось OX в двух точках: x1=5,1 и x2=3,3. В силу симметрии параболы абсцисса её вершины находится ровно посередине между этими точками, то есть xв = (5,1+3,3)/2 = 4,2. Значение функции в этой точке будет являться наименьшим значением выражения (x — 5,1)(x — 3,3).
Ради интереса найдём это значение. После подстановки получаем:
![]() .
.
| 14. При каких значениях x имеет смысл выражение |
Вспоминаем, что под знаком арифметического квадратного корня не могут находиться отрицательные числа. Стало быть область допустимых значений записанного выражения определяется неравенством:
![]()
Это стандартное квадратное неравенство. Решим его. Для этого находим сперва корни соответствующего квадратного уравнения:
![]()
Отмечаем полученные точки на координатной прямой и определяем знаки выражения, которое приравнивали к нулю, на полученных промежутках. С учётом того, что ветви соответствующей параболы направлены вниз, знаки получаются следующие:
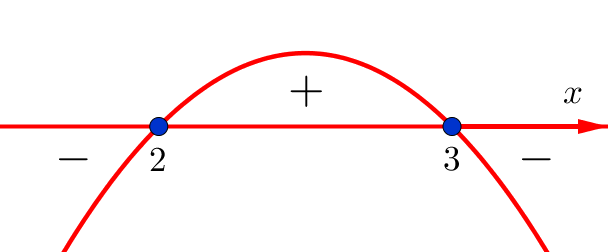
Обе отмеченные точки являются закрашенными, поскольку исходное неравенство является нестрогим. Нас интересует промежуток, в котором функция положительна. Поэтому ответ к данному заданию: ![]() .
.
| 15. Решите неравенство:
|
Сперва преобразуем данное неравенство:
![]()
![]()
Для удобства разделим обе части неравенства на -2. При этом знак неравенства нужно поменять с «больше или равно» на «меньше или равно»:
![]()
Для решения этого неравенства воспользуемся методом интервалов. Выражение, стоящее слева от знака неравенства, равно нулю, когда числитель равен нулю, то есть при ![]() , а знаменатель не равен нулю, то есть при
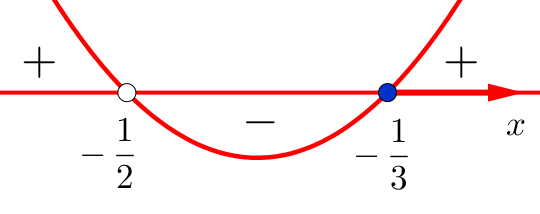
, а знаменатель не равен нулю, то есть при ![]() . Отмечаем эти точки на числовой прямой. Первая точка будет закрашенной, потому что это нестрогое неравенство. Вторая — выколотой, потому что она не входит в область допустимых значений выражения. Далее определяем знаки выражения на полученных промежутках. Для этого подставляем какие-нибудь значения из каждого промежутка в выражение, которое приравнивали к нулю. В результате получаем следующие знаки:
. Отмечаем эти точки на числовой прямой. Первая точка будет закрашенной, потому что это нестрогое неравенство. Вторая — выколотой, потому что она не входит в область допустимых значений выражения. Далее определяем знаки выражения на полученных промежутках. Для этого подставляем какие-нибудь значения из каждого промежутка в выражение, которое приравнивали к нулю. В результате получаем следующие знаки:
Нас интересует промежуток, на котором наше выражение принимается неположительные значения. То есть ответ к заданию: ![]() .
.
| 16. Докажите, что
|
Перенесём правую часть неравенства в левую, поменяв при этом знак:
![]()
Приведём дроби к общему знаменателю и раскроем скобки в числителе первой дроби:
![]()
Вновь раскроем скобки в числителе и приведём подобные слагаемые. В результате приходим к следующему выражению:
![]()
Вынесем в числителе минус за скобки:
![]()
Выражение в скобках можно представить как квадрат разности, используя известную формулу сокращенного умножения:
![]()
Ну и теперь видно, что данное неравенство выполняется при любых значениях ![]() и
и ![]() . Действительно,
. Действительно, ![]() при любых значениях
при любых значениях ![]() и
и ![]() , так как квадрат любого числа не может быть отрицательным. Поэтому
, так как квадрат любого числа не может быть отрицательным. Поэтому ![]() , так как при умножении обеих частей неравенства на отрицательное число -1 нужно поменять знак с
, так как при умножении обеих частей неравенства на отрицательное число -1 нужно поменять знак с ![]() на
на ![]() . Что и требовалось доказать.
. Что и требовалось доказать.
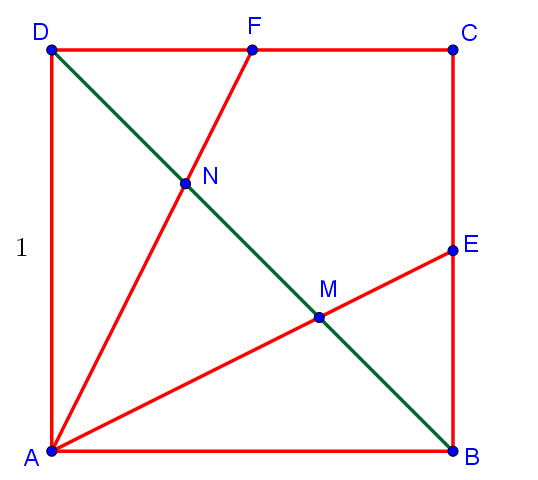
| 17. В квадрате ABCD сторона равна 1. Точки E и F – середины сторон BC и CD. M и N – точки пересечения отрезков AE и AF с диагональю BD. Найдите длину отрезка MN. |
1. По теореме Пифагора для прямоугольного треугольника ABD находим диагональ квадрата BD:
![]()
2. FE — средняя линия треугольника DCB, поэтому длина FE равна половине основания BD в этом треугольнике. Следовательно, ![]() .
.
3. Треугольник DFN подобен треугольнику ANB по двум углам (угол ANB равен углу DNF, так как они вертикальные, а угол DFN равен углу NAB так как они накрест лежащие при параллельных прямых DC, AB и секущей AF).
4. Коэффициент подобия этих треугольников равен отношению DF:AB. При этом AB = DC, так как у квадрата все стороны равны. То есть коэффициент подобия равен DF:DC = 0,5. Из этого следует, что AN:NF = 2:1. То есть AN:AF = 2:3.
5. Аналогично, из подобия треугольников EMB и AMD следует, что AM:AE = 2:3.
6. Треугольник ANM подобен треугольнику AFE по углу FAE, который является общим для обоих треугольников, и сходственным сторонам: AN:AF = AM:AE = 2:3. Следовательно имеет место соотношение:
![]()
Это ответ. Безусловно, возможны и другие варианты решения этого задания. Если у вас есть более интересные решения, пишите их в комментариях.
В этой статье мы разобрали один из вариантов, предлагавшихся абитуриентам лицея «Вторая школа» в качестве вступительного по математике в 2017 году. Если вы без проблем смогли решить все задания самостоятельно без ошибок с первого раза, то вы вполне готовы к поступлению в этот лицей. Если же эти задания вызвали серьёзные затруднения, то вы всегда можете обратиться к помощи профессионального репетитора, который поможет вам разобраться в хитросплетениях математики и подготовиться к вступительному в лицей №2. Удачи!

![Rendered by QuickLaTeX.com \[ \dfrac{\left(12x^2\right)^4}{4^2\left(18x^3\right)^3} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-40b7b385e05a7220a878e19dbef9864c_l3.png)
![Rendered by QuickLaTeX.com \[ \left(\frac{a+b}{2}\right)^2\leqslant \frac{a^2+b^2}{2}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-7140b2dd490f76e52181cda9237446aa_l3.png)