
Для многих одаренных детей поступление в школу «Интеллектуал» — это шанс развить свои способности и получить больше систематизированных знаний по определенному предмету, которые помогут получить высокие баллы при сдаче ЕГЭ, а также дополнительных вступительных экзаменов в выбранный ВУЗ. В этом заведении могут учиться ребята, проживающие не только в Москве, но и в Подмосковье: у них есть возможность оставаться в интернате, рассчитанном на 140 человек.
Государственная специализированная школа «Интеллектуал» была основана в 2002 году Евгением Владимировичем Маркеловым – российским педагогом-новатором, кандидатом исторических наук и археологом. Он назвал свое заведение экспериментальным, так как в основу обучения закладывались новые принципы, отличные от тех, которые применяют в общеобразовательных учреждениях. В первый год обучения здесь было всего 70 учеников 5-8 классов. Сейчас в «Интеллектуале» насчитывается 410 учеников 5-11 классов.
Эта школа стала основной площадкой по проблемам работы с одаренными детьми. Здесь не только четко организован учебный процесс, но и создана уютная домашняя атмосфера, благодаря чему обучение приносит только удовольствие.
Особенности обучения в школе-интернате «Интеллектуал»
Учебный процесс в этом образовательном учреждении построен на качественно новом подходе: основной принцип состоит в том, чтобы дети сами выбирали те предметы, которые им интересны и в которые они хотели бы углубиться. Девиз школы «Интеллектуал»: «Пусть дети учатся тому, чему хотят, и столько, сколько хотят».
Ученик может выбрать несколько таких предметов и максимально сконцентрироваться на их изучении. В процессе преподавания педагоги используют методику, благодаря которой учащиеся не только полноценно усваивают материал, но и совершенствуют навыки, тренируют память, учатся логически мыслить.
Перечень предметов, среди которых ребенок может выбрать интересующие именно его:
- математика;
- физика;
- химия;
- биология;
- история;
- обществознание;
- география;
- русский язык;
- иностранные языки (английский, немецкий);
- лингвистика;
- искусство;
- робототехника, IT;
- психология;
- спорт.
Учащиеся 4-11 классов могут выбрать спецкурс по:
- химии;
- филологии;
- физкультуре;
- физике;
- социально-экономическим дисциплинам;
- психологии;
- мировой художественной культуре;
- математике;
- информатике;
- истории;
- географии;
- иностранным языкам;
- биологии.
Преподавательский состав

Директором школы для одаренных детей с 2016 года и по сей день является Запольский Илья Алексеевич.
В учебном заведении работают 79 педагогов, 8 из которых имеют ученую степень.
Преподавание находится на высоком уровне. Подтверждение этому – не только многочисленные положительные отзывы об образовательной организации, но и результаты участия учеников школы «Интеллектуал» в различных предметных олимпиадах, в том числе международных:
- 2008 год – серебро (Лингвистика).
- 2010 год – золото (Информатика, Лингвистика).
- 2017 год – золото (Информатика).
- 2018 год – серебро (Лингвистика, Информатика).
После завершения этой школы многие ученики поступили в престижные отечественные (МГУ, НИУ ВШЭ, РУДН, МГИМО) и зарубежные ВУЗы.
Поступление в школу «Интеллектуал»: что потребуется от соискателей
Поступление в школу «Интеллектуал» потребует от ребенка усилий и упорного труда: сюда берут только самых талантливых. Нагрузки очень серьезные. Именно поэтому перед поступлением нужно трезво оценить свои возможности: образовательная программа этой школы гораздо сложнее той, которая применяется в средних общеобразовательных учреждениях.
Для того, чтобы стать учеником школы «Интеллектуал», нужно пройти конкурс, состоящий из трех этапов:
- Проверка знаний абитуриента в области русского языка, математики и двух предметов на выбор, в зависимости от выбранного профиля.
- Защита творческого или исследовательского проекта, который может быть выполнен в разных формах (например, аналитическая или прикладная работа). Тематика зависит от того, на какую кафедру зарегистрировался абитуриент.
- Пробная учеба в школе в течение недели.
Для участия в первом туре необходимо зарегистрироваться на сайте школы. Для тех, кто поступает в среднюю школу, экзамен состоит из теста и задания на выбор. Для поступающих в старшую школу испытания зависят от выбранного профиля. От результатов первого тура зависит, сможет ли абитуриент пройти на второй и третий отборочные этапы. День творческих работ (защита проекта) назначается отдельно.
Подготовке к поступлению нужно уделить особое внимание. Так как в школу принимают только самых талантливых и перспективных абитуриентов, вступительные экзамены отличаются высокой сложностью. Особенно это касается математики и физики. Рассчитывать сдать их, опираясь только на полученные в общеобразовательной школе знания, не стоит. Если вы хотите успешно сдать экзамен в школу «Интеллектуал», вам стоит пройти индивидуальную подготовку с репетитором.
Ниже для примера приведён разбор демоварианта вступительного экзамена в 10 класс по математике. Попробуйте решить эти задачи самостоятельно, это станет для вас полезной тренировкой.
Разбор демоверсии профильного экзамена по алгебре для поступающих в 10 класс
| Задание 1. Решите уравнение |
Рассмотрим 3 случая:
- При
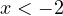 оба модуля раскрываются со отрицательным знаком, поэтому получается уравнение
оба модуля раскрываются со отрицательным знаком, поэтому получается уравнение  , из которого находим, что
, из которого находим, что 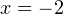 . Но этот корень не удовлетворяет условию
. Но этот корень не удовлетворяет условию 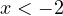 .
. - При
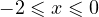 первый модуль раскрывается с отрицательным знаком, а второй — с положительным, поэтому получается уравнение
первый модуль раскрывается с отрицательным знаком, а второй — с положительным, поэтому получается уравнение 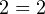 , которое верно всегда. То есть подходит любое значение
, которое верно всегда. То есть подходит любое значение 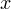 , удовлетворяющее условию
, удовлетворяющее условию 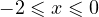 .
. - При
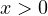 оба модуля раскрываются с положительным знаком, поэтому получается уравнение
оба модуля раскрываются с положительным знаком, поэтому получается уравнение 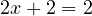 , из которого находим, что
, из которого находим, что 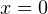 . Но этот корень не удовлетворяет условию
. Но этот корень не удовлетворяет условию 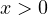 .
.
Ответ: ![]() .
.
| Задание 2. Решите уравнение |
Обратим внимание, что ![]() является корнем этого уравнения. Значит, многочлен слева от знака равенства должен разделиться на
является корнем этого уравнения. Значит, многочлен слева от знака равенства должен разделиться на ![]() . Разделим столбиком:
. Разделим столбиком:
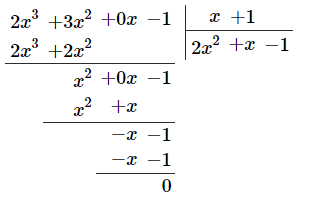
То есть исходное уравнение эквивалентно следующему:
![]()
Уравнение ![]() имеет два корня:
имеет два корня: ![]() и
и ![]() .
.
Ответ: ![]() и
и ![]() .
.
| Задание 3. Решите неравенство
|
Обратим внимание, что ![]() , поэтому исходное неравенство эквивалентно следующему:
, поэтому исходное неравенство эквивалентно следующему:
![]()
![]()
![]()
Последнее неравенство выполняется всегда, кроме ![]() .
.
Ответ: ![]() .
.
| Задание 4. Решите неравенство
|
Преобразуем неравенство:
![]()
![]()
![Rendered by QuickLaTeX.com \[ \dfrac{(x-1)\left(x+1-\sqrt{13-x^2}\right)}{\sqrt{13-x^2}}\geqslant 0 \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ff71f66e5c6e9d2dabe6c3d5fc35f62e_l3.png)
Область допустимых значений задаётся неравенством ![]() , то есть
, то есть ![]() . Рассмотрим два случая:
. Рассмотрим два случая:
- Если
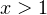 , то
, то 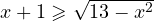 . То есть
. То есть 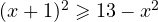 или
или 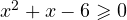 . Решением последнего неравенства, с учётом всех ограничений, является промежуток
. Решением последнего неравенства, с учётом всех ограничений, является промежуток 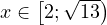 .
. - Если
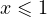 , то
, то 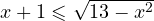 . Данное неравенство выполняется для всех
. Данное неравенство выполняется для всех 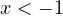 из области допустимых значений, так как левая часть при этом отрицательна, а правая — положительна. При
из области допустимых значений, так как левая часть при этом отрицательна, а правая — положительна. При 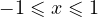 после возведения обеих частей в квадрат получаем
после возведения обеих частей в квадрат получаем 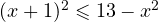 или
или 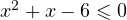 . Полученное неравенства выполняется для всех
. Полученное неравенства выполняется для всех ![Rendered by QuickLaTeX.com x\in[-1;1]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-03e3c2474493c24d53eea4a6e9d97c93_l3.png) .
.
Объединяя полученные решения, получаем окончательный ответ: ![]() .
.
| Задание 5. а) Постройте график функции б) Исследуйте зависимость количества различных действительных корней уравнения |
а) График функции ![]() получаем из графика функции
получаем из графика функции ![]() путём стандартных преобразований (подробнее смотрите в прилагаемом видео):
путём стандартных преобразований (подробнее смотрите в прилагаемом видео):
Получается следующий график:
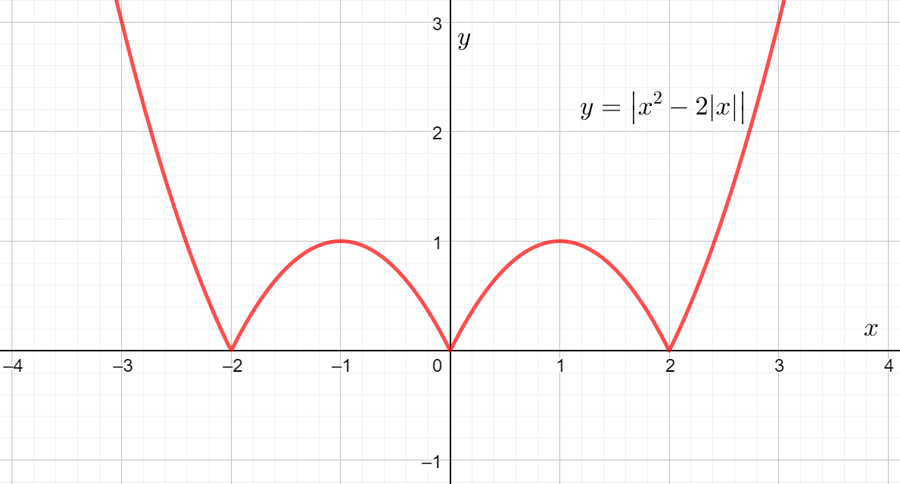
б) Исследуем, сколько точек пересечения изображённый график имеет с прямой ![]() , параллельной оси OX, в зависимости от значения параметра
, параллельной оси OX, в зависимости от значения параметра ![]() . В результате получаем ответ:
. В результате получаем ответ:
При ![]() уравнение не имеет корней, при
уравнение не имеет корней, при ![]() уравнение имеет 3 различных действительных корня, при
уравнение имеет 3 различных действительных корня, при ![]() уравнение имеет 6 различных действительных корней, при
уравнение имеет 6 различных действительных корней, при ![]() уравнение имеет 4 различных действительных корня, при
уравнение имеет 4 различных действительных корня, при ![]() уравнение имеет 2 различных действительных корня.
уравнение имеет 2 различных действительных корня.
| Задание 6. Изобразите на плоскости множество точек |
Изобразим на координатной плоскости прямую ![]() или
или ![]() , а также кривую
, а также кривую ![]() или
или ![]() . Далее в каждой области, на которые разобьют плоскость эти линии, выберем точку, подставим её координаты у левую часть исходного неравенства. Если неравенство при этом выполняется, то отмечаем область, в которой находится данная точка, если нет — не отмечаем. В результате все отмеченные области составят искомое множество. Ответ получается следующий:
. Далее в каждой области, на которые разобьют плоскость эти линии, выберем точку, подставим её координаты у левую часть исходного неравенства. Если неравенство при этом выполняется, то отмечаем область, в которой находится данная точка, если нет — не отмечаем. В результате все отмеченные области составят искомое множество. Ответ получается следующий:
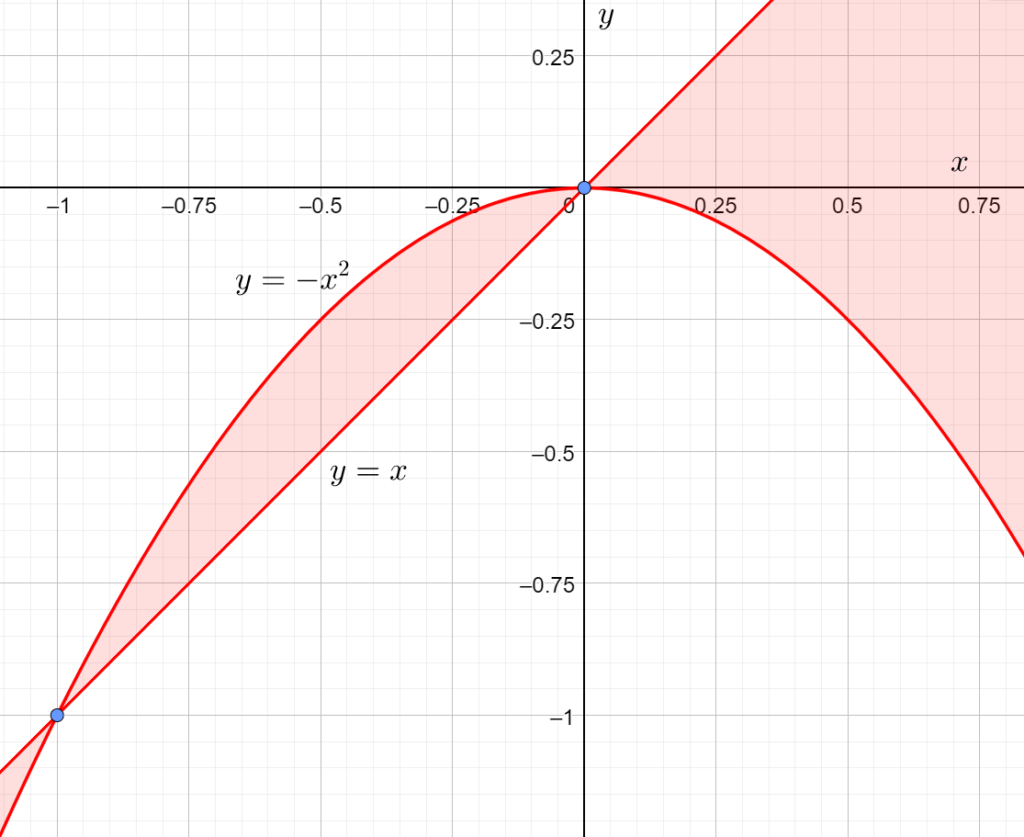
| Задание 7. При каких |
Рассмотрим функцию ![]() . Выделим три случая:
. Выделим три случая:
- При
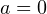 уравнение имеет только 1 корень. Этот случай не походит.
уравнение имеет только 1 корень. Этот случай не походит. - При
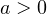 ветви соответствующей параболы направлены вверх. Нужно, чтобы эта парабола пересекла ось OX в двух точках, одна из которых расположена левее точки 2, а другая — правее. Требуемое условие задаётся в этом случае неравенством
ветви соответствующей параболы направлены вверх. Нужно, чтобы эта парабола пересекла ось OX в двух точках, одна из которых расположена левее точки 2, а другая — правее. Требуемое условие задаётся в этом случае неравенством 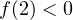 . То есть
. То есть 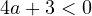 или
или 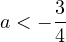 . Из этого множества ни одно значение
. Из этого множества ни одно значение 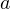 не удовлетворяет условию
не удовлетворяет условию 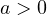 .
. - При
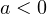 ветви соответствующей параболы направлены вниз. Нужно, чтобы эта парабола пересекла ось OX в двух точках, одна из которых расположена левее точки 2, а другая — правее. Требуемое условие задаётся в этом случае неравенством
ветви соответствующей параболы направлены вниз. Нужно, чтобы эта парабола пересекла ось OX в двух точках, одна из которых расположена левее точки 2, а другая — правее. Требуемое условие задаётся в этом случае неравенством 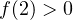 . То есть
. То есть 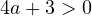 или
или 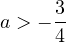 . Поскольку мы рассматриваем только значения
. Поскольку мы рассматриваем только значения 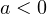 , то в этом случае
, то в этом случае 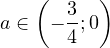 .
.
Ответ: ![]() .
.
| Задание 8. Два туриста вышли из пункта А в пункт В одновременно, причем первый турист каждый километр пути проходит на 5 минут быстрее второго. Первый, пройдя пятую часть пути, вернулся в А за случайно забытой тушенкой и, пробыв там 10 минут, снова пошел в В. В результате в пункт В оба туриста пришли одновременно. Каково расстояние от А до В, если второй турист прошел его за 2,5 часа? |
Пусть скорость второго туриста равна ![]() м/мин. Тогда скорость первого туриста такова, что выполняется уравнение:
м/мин. Тогда скорость первого туриста такова, что выполняется уравнение: ![]() . Значит,
. Значит, ![]() .
.
Пусть расстояние от A до B равна ![]() . Время движения второго туриста
. Время движения второго туриста ![]() мин. Время движения первого туриста
мин. Время движения первого туриста ![]() мин. Первый турист прошёл в совокупности
мин. Первый турист прошёл в совокупности ![]() . Тогда имеет место система уравнений:
. Тогда имеет место система уравнений:
![Rendered by QuickLaTeX.com \[ \begin{cases} \dfrac{200x}{x+200}\cdot 150 = S \\ 140x=\dfrac{7}{5}S \end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-49feb3d289378fe8c1d07b34ec937d1a_l3.png)
Ненулевым решением полученной системы является пара: ![]() и
и ![]() .
.
Ответ: 10 км.
| Задание 9. Докажите, что при всех натуральных |
1. Для ![]() получаем 50, что кратно 25.
получаем 50, что кратно 25.
2. Пусть верно для ![]() . То есть
. То есть ![]() кратно 25.
кратно 25.
3. Докажем, что верно для ![]() . Подставляем и получаем:
. Подставляем и получаем:
![]()
![]()
По предположению индукции первое слагаемое в полученном выражении кратно 25, а второе слагаемое кратно 25, так как 100 кратно 25. Значит, всё полученное выражение кратно 25. Тогда по методу математической индукции утверждение верно для любого натурального ![]() . Что и требовалось доказать.
. Что и требовалось доказать.
| Задание 10. Найдите сумму
|
Преобразуем данную сумму:
![]()
![Rendered by QuickLaTeX.com \[ =\dfrac{2^2\cdot\left(\left(2^2\right)^n-1\right)}{2^2-1}+\dfrac{\dfrac{1}{2^2}\cdot\left(\left(\dfrac{1}{2^2}\right)^n-1\right)}{\dfrac{1}{2^2}-1} +2n =\]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-fd99cb8d8a4ae8552cafbc4906f7d232_l3.png)
![]()
Примеры исследовательских заданий
| Задание 11. Турист вышел из своей палатки, прошел 5 км на юг, 5 км на восток и 5 км на север, после чего снова оказался у своей палатки. Где такое могло произойти? |
Такое могло произойти если:
- Турист находился изначально точно на Северном полюсе. Тогда любое начальное направление движения будет на юг. После похождения 5 км на юг турист пройдёт 5 км на восток, затем развернётся и пройдёт 5 км на север, после чего вновь окажется на Северном полюсе.
- Если турист находится на параллели около Южного полюса, пройдя от которой по меридиану в направлении Южного полюса, турист оказывается на параллели, длина которой ровно 5 км. Тогда после прохождения 5 км на юг турист развернётся и пойдёт 5 км на восток, обойдёт всю эту параллель, вернётся в ту же точку (на тот же меридиан), повернётся и пройдёт ещё 5 км на север, в результате чего окажется в исходной точке. Возможен также вариант, что длина параллели будет 5/2 км. Тогда турист обойдёт эту параллель дважды. Или 5/3 км — тогда трижды и т.д. Получается счётное множество параллелей около Южного полюса.
| Задание 12. В Скверной стране все колеса квадратные. Квадратное колесо катится по ровной дороге без проскальзывания. Нарисуйте траекторию оси скверного колеса. (Ось проходит через центр колеса). Из каких кривых она состоит? |
Траектория движения оси квадратного колеса отмечена на рисунке сплошной синей линией:
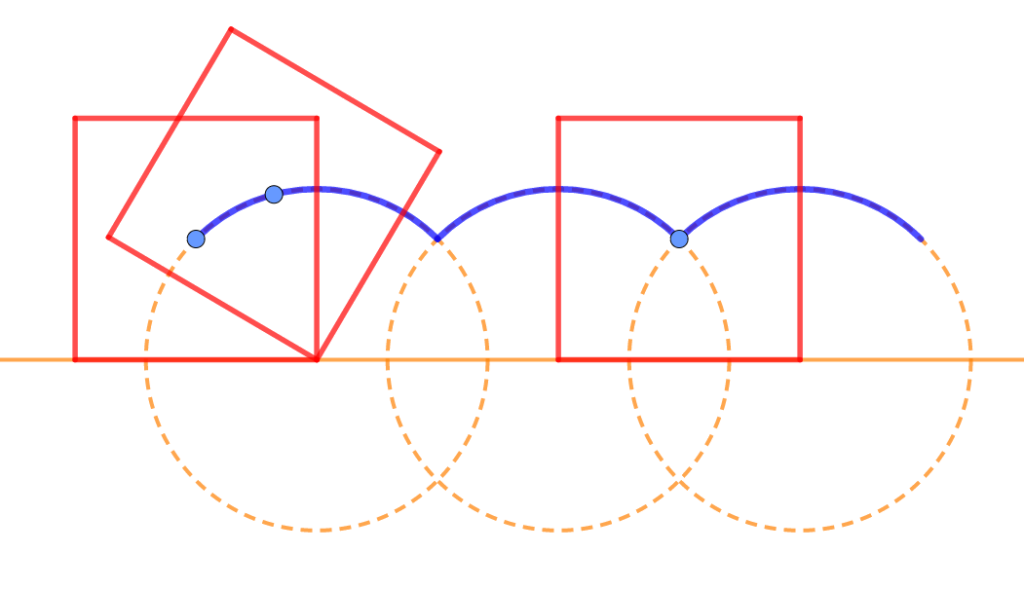
Разбор задач к демоверсии по геометрии для поступающих в 10 класс
| Задание 1. В равнобедренном треугольнике ABC с основанием AC медианы пересекаются в точке O. Найдите площадь треугольника ABC, если OA = 13 см и OB = 10 см. |
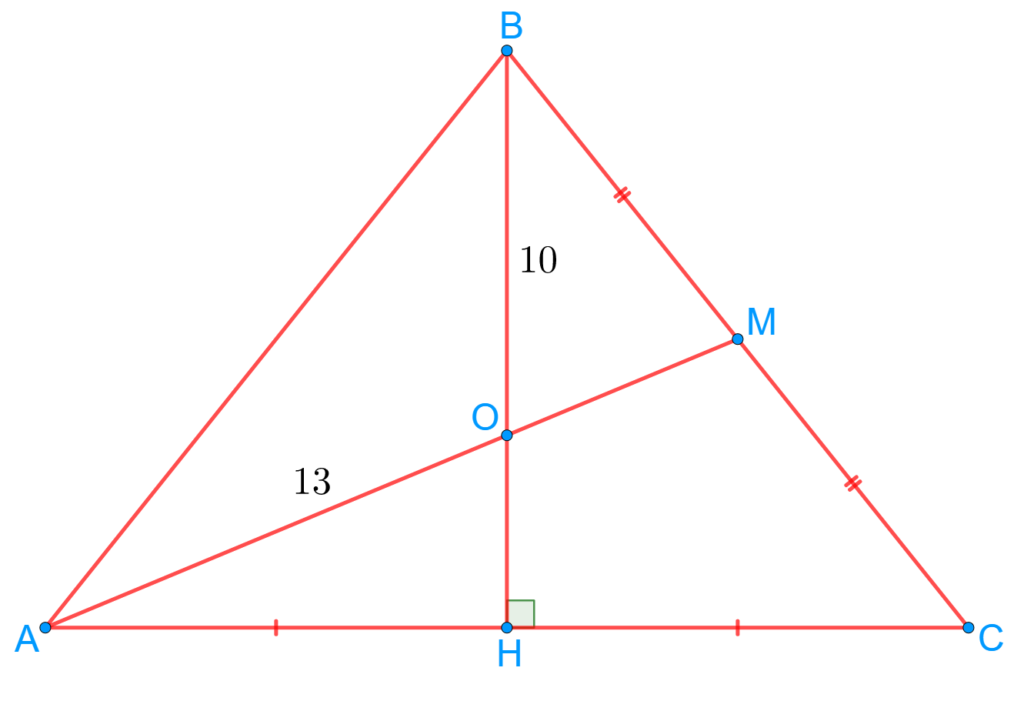
По свойству медиан треугольника получаем, что ![]() , поэтому
, поэтому ![]() . Медиана BH является одновременно и высотой, поскольку она проведена в равнобедренном треугольнике к основанию, поэтому треугольник AOH является прямоугольным. Используя теорему Пифагора для этого треугольника, находим, что
. Медиана BH является одновременно и высотой, поскольку она проведена в равнобедренном треугольнике к основанию, поэтому треугольник AOH является прямоугольным. Используя теорему Пифагора для этого треугольника, находим, что ![]() . Тогда
. Тогда ![]() . Кроме того,
. Кроме того, ![]() . Значит, площадь треугольника ABC равна
. Значит, площадь треугольника ABC равна ![]() .
.
Ответ: 180.
| Задание 2. Диагонали трапеции пересекаются под прямым углом. Докажите, что средняя линия равна отрезку, соединяющему середины оснований. |
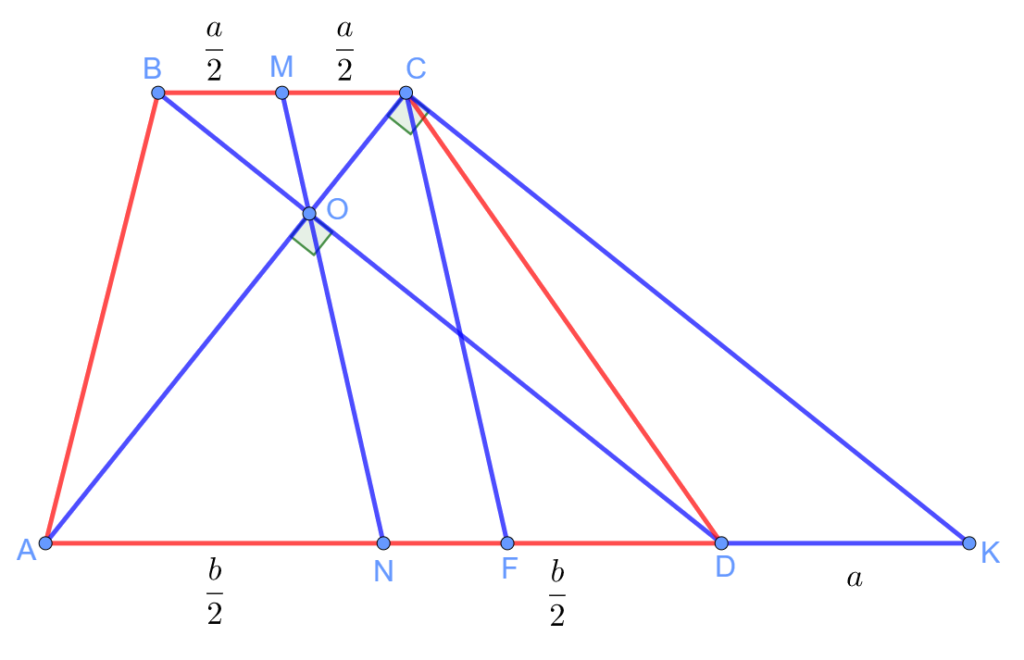
Пусть ![]() и
и ![]() . Выполним дополнительное построение. Проведём через точку C прямую, параллельную диагонали BD. Точку пересечения этой прямой с прямой AD обозначим K. Тогда четырёхугольник BCKD является параллелограммом, так как его стороны попарно параллельны. Значит,
. Выполним дополнительное построение. Проведём через точку C прямую, параллельную диагонали BD. Точку пересечения этой прямой с прямой AD обозначим K. Тогда четырёхугольник BCKD является параллелограммом, так как его стороны попарно параллельны. Значит, ![]() . Тогда
. Тогда ![]() .
.
Обозначим середину отрезка AK буквой F. Тогда ![]() . По свойству медианы прямоугольного треугольника, проведённой из вершины прямого угла,
. По свойству медианы прямоугольного треугольника, проведённой из вершины прямого угла, ![]() . То есть CF равна длине средней линии этой трапеции. Осталось доказать, что CF = MN.
. То есть CF равна длине средней линии этой трапеции. Осталось доказать, что CF = MN.
Действительно, ![]() . То есть NF = MC. Значит, в четырёхугольнике MCFN противоположные стороны MC и NF равны и параллельны. Значит, этот четырёхугольник является параллелограммом. То есть
. То есть NF = MC. Значит, в четырёхугольнике MCFN противоположные стороны MC и NF равны и параллельны. Значит, этот четырёхугольник является параллелограммом. То есть ![]() . Этому же значению равна длина средней линии этой трапеции. Что и требовалось доказать.
. Этому же значению равна длина средней линии этой трапеции. Что и требовалось доказать.
| Задание 3. В треугольник ABC (AB = 5, AC = 8, BC = 7) вписана окружность. K — точка касания этой окружности со стороной AC. Найдите: а) разложение вектора |
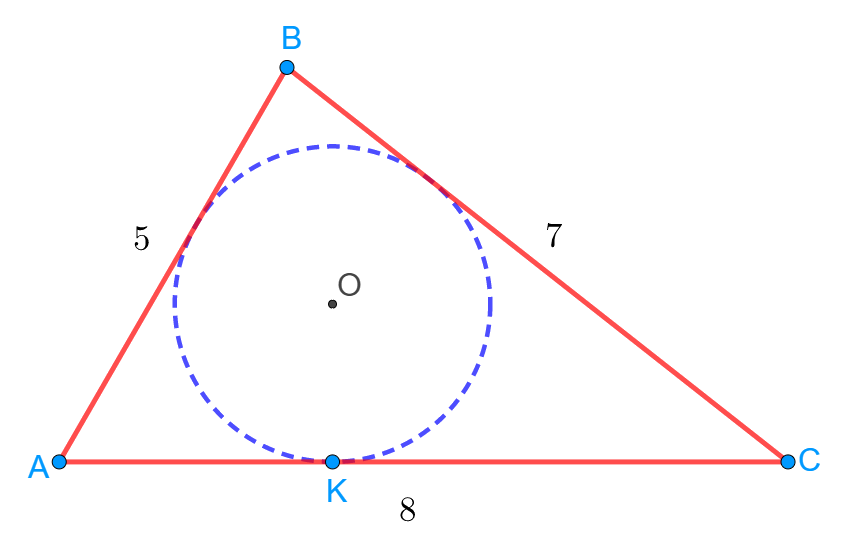
а) ![]() , откуда
, откуда ![]() .
.
в) Применим теорему косинусов для треугольника ABC: ![]() , откуда
, откуда ![]() . Значит,
. Значит, ![]() .
.
б) ![]() .
.
г) Полупериметр треугольника ![]() . По формуле Герона находим площадь треугольника ABC:
. По формуле Герона находим площадь треугольника ABC: ![]() . Тогда радиус вписанной окружности равен
. Тогда радиус вписанной окружности равен ![]() .
.
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника. Значит, получаем, что ![]() . Тогда
. Тогда ![]() , откуда
, откуда ![]() . Длину BK находим по теореме косинусов, записанной для треугольника ABK:
. Длину BK находим по теореме косинусов, записанной для треугольника ABK: ![]() . Итак, получаем, что
. Итак, получаем, что ![]() .
.
д) ![]() , откуда
, откуда ![]() .
.
Ответ: а) ![]() ; б) 20; в)
; б) 20; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
Поступление в школу «Интеллектуал» с репетитором
Поступление в школу «Интелектуал» с репетитором, специализирующемся на конкретной дисциплине, имеет следующие преимущества:
- Возможность решать варианты тестов прошлых вступительных кампаний, чтобы иметь представление о том, какого рода вопросы могут ожидать на экзамене.
- Персональный подход к каждому ученику и выбор оптимального темпа обучения.
- Доступное изложение нового материала, донесение до ученика даже самых сложных вещей понятным языком.
- Наличие собственной, наработанной годами методики преподавания.
Чтобы добиться хороших результатов, подготовку стоит начать как можно раньше. Например, уже летом, за год до поступления в школу «Интеллектуал».
Если вам требуется подготовка к вступительным экзаменам в школу «Интеллектуал», обращайтесь ко мне. Я являюсь профессиональным репетитором по математике и физике и не первый год успешно осуществляю такую подготовку, причём работаю не только со старшеклассниками, но и с учениками из младшей школы. Мои контакты вы найдёте на этой странице.
Материал подготовил репетитор по математике и физике в Москве Сергей Валерьевич

![Rendered by QuickLaTeX.com \[ \left(2+\dfrac{1}{2}\right)^2+\left(4+\dfrac{1}{4}\right)^2+\dots+\left(2^n+\dfrac{1}{2^n}\right)^2 \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-901549af87cafeb6762f92f0a0764067_l3.png)