Площадь эллипса без интеграла

Прочитав эту статью, вы узнаете, как доказать формулу площади эллипса без использования интеграла. В интернете есть множество статьей и видео о том, как доказывается формула площади эллипса. Однако, в основном все эти доказательства сводятся к использованию интеграла (определённого, двойного или криволинейного интеграла по замкнутому контуру). Данная статья написана для тех, кто интересуется, как можно доказать формулу площади эллипса без интеграла.

Определение эллипса

Эллипс — это геометрическое место всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек одинакова и больше расстояния между этими двумя точками. Данные точки называют фокусами эллипса. Изобразим эллипс в прямоугольной декартовой системе координат:

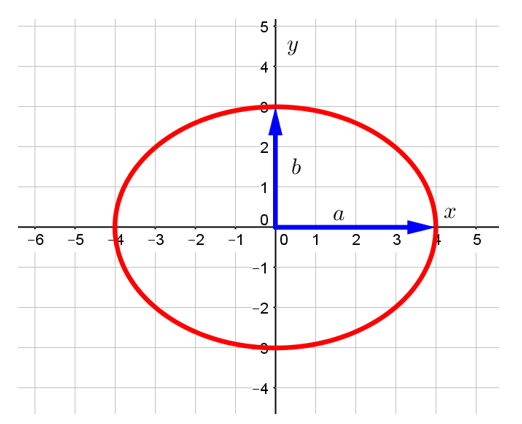
Отмеченные на рисунке буквами и отрезки называются большой и малой полуосью эллипса, соответственно. В случае изображённого на рисунке эллипса и .

Уравнение эллипса

В каноническом виде уравнение эллипса в прямоугольной декартовой системе координат с центром в начале координат имеет вид:

   

Обратим внимание, что в случае, когда , получается классическое уравнение окружности с центром в начале координат и радиусом :

   

Это говорит о том, что окружность — это частный случай эллипса, когда обе его полуоси одинаковы и равны радиусу этой окружности.

Формула площади эллипса

Формула, выражающая площадь эллипса через его полуоси, очень проста и изящна:

   

И вновь, в случае, когда обе полуоси эллипса одинаковы, то есть , формула принимает вид:

   

Это широко известная формула площади круга.

Главный вопрос: «Как получить формулу площади эллипса без использования интеграла?»

Вывод формулы площади эллипса без интеграла

Выполним следующее преобразование для каждой точки эллипса:

   

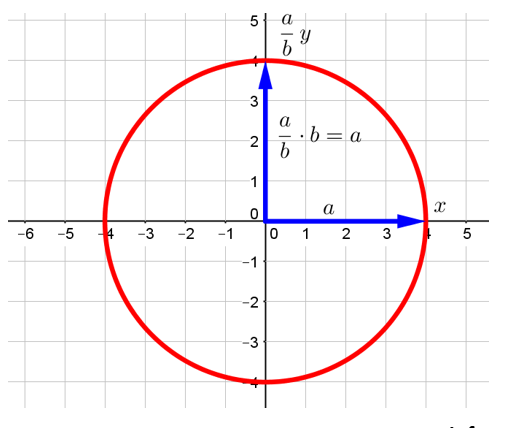
То есть как бы перейдём в новую систему координат, в которой абсциссы каждой точки эллипса остаются старыми, а ординаты по отношению к старой системе координат возрастают в число раз. С случае изображённого на рисунке эллипса , поэтому этот эллипс после такого преобразования вытянется вдоль оси Y так, что превратится в окружность! Изобразим эту окружность в сетке старой системы координат:

Радиус это окружности равен . Действительно, малая полуось была равна , но после умножения на коэффициент она стала равна . Значит, площадь этой окружности равна . Но поскольку все длины вдоль оси Y были увеличены в раз, а все длины вдоль оси X остались неизменными, то площадь фигуры также была увеличена в раз. То есть для возвращения к площади исходного эллипса площадь полученной окружности нужно разделить на коэффициент :

   

Что и требовалось доказать. Получили площадь эллипса без интеграла.

Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич