В данной статье рассказано о том, как найти модуль равнодействующей сил, действующих на тело. Репетитор по математике и физике объяснит вам, как найти суммарный вектор равнодействующей сил по правилу параллелограмма, треугольника и многоугольника. Материал разобран на примере решения задачи из ЕГЭ по физике.
Как найти модуль равнодействующей силы
| Сила, которая оказывает на материальную точку такое же действие, как и несколько других сил, называется равнодействующей этих сил. Для нахождения вектора равнодействующей силы необходимо геометрически (векторно) сложить все силы, которые действуют на материальную точку. |
Напомним, что сложить векторы геометрически можно с помощью одного из трех правил: правила параллелограмма, правила треугольника или правила многоугольника. Разберём каждое из этих правил в отдельности.
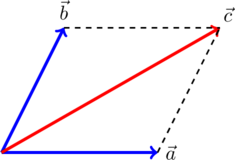
1. Правило параллелограмма. На рисунке по правилу параллелограмма складываются векторы ![]() и
и ![]() . Суммарный вектор есть вектор
. Суммарный вектор есть вектор ![]() :
:
Если векторы ![]() и
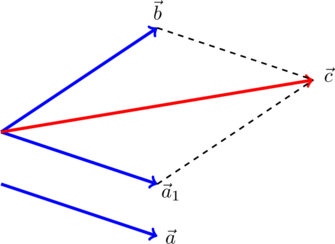
и ![]() не отложены от одной точки, нужно заменить один из векторов равным и отложить его от начала второго вектора, после чего воспользоваться правилом параллелограмма. Например, на рисунке вектор
не отложены от одной точки, нужно заменить один из векторов равным и отложить его от начала второго вектора, после чего воспользоваться правилом параллелограмма. Например, на рисунке вектор ![]() заменен на равный ему вектор
заменен на равный ему вектор ![]() , и
, и ![]() :
:
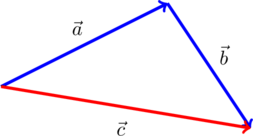
2. Правило треугольника. На рисунке по правилу треугольника складываются векторы ![]() и
и ![]() . В сумме получается вектор
. В сумме получается вектор ![]() :
:
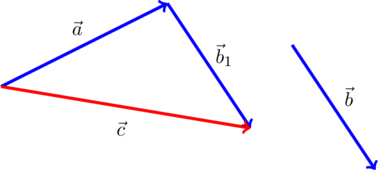
Если вектор ![]() отложен не от конца вектора
отложен не от конца вектора ![]() , нужно заменить его равным и отложенным от конца вектора
, нужно заменить его равным и отложенным от конца вектора ![]() , после чего воспользоваться правилом треугольника. Например, на рисунке вектор
, после чего воспользоваться правилом треугольника. Например, на рисунке вектор ![]() заменен равным ему вектором
заменен равным ему вектором ![]() , и
, и ![]() :
:
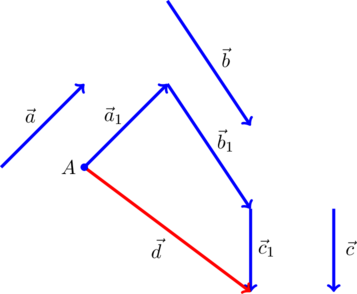
3. Правило многоугольника. Для того, чтобы сложить несколько векторов по правилу параллелограмма, необходимо от произвольной точки ![]() отложить вектор, равный первому складываемому вектору, от его конца отложить вектор, равный второму складываемому вектору, и так далее. Суммарным будет вектор, проведенный из точки
отложить вектор, равный первому складываемому вектору, от его конца отложить вектор, равный второму складываемому вектору, и так далее. Суммарным будет вектор, проведенный из точки ![]() в конец последнего отложенного вектора. На рисунке
в конец последнего отложенного вектора. На рисунке ![]() :
:
Задача на нахождение модуля равнодействующей силы
Разберем задачу на нахождение равнодействующей сил на конкретном примере из демонстрационного варианта ЕГЭ по физике 2016 года.
| Задача 2. На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Чему равен модуль равнодействующей силы?
|
Для нахождения вектора равнодействующей сил найдём геометрическую (векторную) сумму всех изображенных сил, используя правило многоугольника. Упрощенно говоря (не вполне корректно с математической точки зрения), каждый последующий вектор нужно отложить от конца предыдущего. Тогда суммарный вектор будет исходить из точки, из который отложен первоначальный вектор, и приходить в точку, где заканчивается последний вектор:
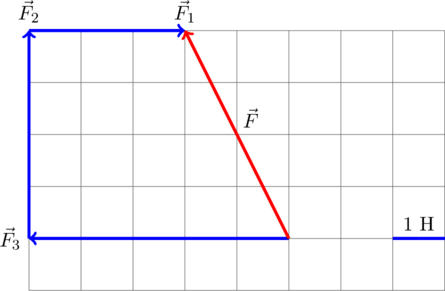
Требуется найти модуль равнодействующей сил, то есть длину получившегося вектора. Для этого рассмотрим вспомогательный прямоугольный треугольник ![]() :
:
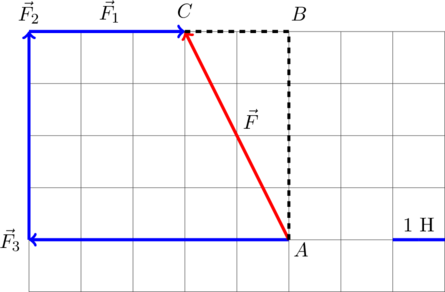
Требуется найти гипотенузу ![]() этого треугольника. «По клеточкам» находим длину катетов:
этого треугольника. «По клеточкам» находим длину катетов: ![]() Н,
Н, ![]() Н. Тогда по теореме Пифагора для этого треугольника получаем:
Н. Тогда по теореме Пифагора для этого треугольника получаем: ![]() Н. То есть искомый модуль равнодействующей сил равен
Н. То есть искомый модуль равнодействующей сил равен ![]() Н.
Н.
Итак, сегодня мы разобрали, как находить модуль равнодействующей силы. Задачи на нахождение модуля равнодействующей силы встречаются в вариантах ЕГЭ по физике. Для решения этих задач необходимо знать определение равнодействующей сил, а также уметь складывать векторы по правилу параллелограмма, треугольника или многоугольника. Стоит немного потренироваться, и вы научитесь решать эти задачи легко и быстро. Удачи вам в подготовке к ЕГЭ по физике!
Репетитор по физике на Юго-Западной
Сергей Валерьевич

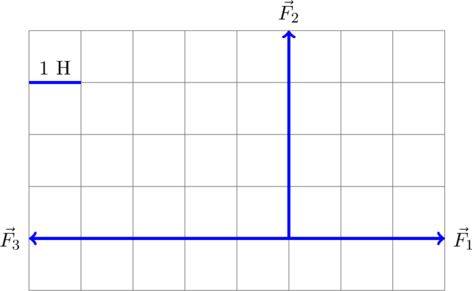
Как найти равнодействующую 4 сил, направленные крестом?
Если силы одинаковые, то нужно просто модуль одной умножить на корень из двух. И тогда получится модуль равнодействующей силы.
как найти вектор 3 равнодействующих сил?
Нужно сперва сложить два любых вектора сил, а затем сложить с результатом 3й вектор.
Как найти равнодействующую 2017 сил
Сложить все их векторно. Напишите полную формулировку задачи, тогда смогу ответить более конкретно.
Чему равна равнодействующая трех сил? Как в задаче 2 в право, влево и наверх?
Решение же написано.
Как найти равнодействующую трёх сил если не дано сколько они, они исходят из одной точки и между ними 60°
Нужен рисунок хотя бы. Так получается задача в стиле «найди то, не знаю что».
Векторы m, n, p приложенны к одной точке и имеют взаимоперпендикулярное направление. m=2 n=10 p=11
Нужно вычислить величину их раанодействующей
Корень(m^2+n^2+p^2)=15
Как найти равнодействующую 2019 равных по молодую сил, приложенных к одной точке и расположенных в одной плоскости, если углы между всеми соседними силами равны между собой.
Если равнодействующая и одна из двух сил приложенных к материальной точке под углом 90 равны соответственно 5 и 4 , то модуль второй силы равен
Найти равнодействующую
20
равных по модулю сил, приложенных к одной точке и расположенных в одной плоскости, если углы между всеми соседними силами равны между собой.
как определить модуль и направление равнодействущей силы если векторы f1 и f2 а из модули 5H и 3H
как найти вектор 217447 сил