Зачастую студенты предпочитают откладывать сдачу всех работ на самый последний момент. Поэтому для многих преподавателей работа в авральном режиме во время экзаменационной сессии стала уже привычной. Предлагаю вашему вниманию решение контрольной работы по математической статистике для II курса Московского отделения Всероссийского Заочного Финансово-Экономического Института (ВЗФЭИ).
Задача 1. С целью определения средней продолжительности обслуживания клиентов в пенсионном фонде, число клиентов которого очень велико, по схеме собственно-случайной бесповторной выборки проведено обследование 100 клиентов. Результаты обследования представлены в таблице:
| Время обслуживания, мин. | <2 | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 | >12 | Итого |
| Число клиентов | 6 | 10 | 21 | 39 | 15 | 6 | 3 | 100 |
Найти:
- границы, в которых с вероятностью 0,9946 заключено среднее время обслуживания всех клиентов пенсионного фонда;
- вероятность того, что доля всех клиентов фонда с продолжительностью обслуживания менее 6 минут отличается от доли таких клиентов в выборке не более чем на 10% (по абсолютной величине);
- объем повторной выборки, при котором с вероятностью 0,9907 можно утверждать, что доля всех клиентов фонда с продолжительностью обслуживания менее 6 минут отличается от доли таких клиентов в выборке не более чем на 10% (по абсолютной величине).
Решение. Находим выборочную среднюю:
![Rendered by QuickLaTeX.com \[ \overline{x}=\frac{1}{n}\sum_{i=1}^7{\overline{x_i}\cdot n_i}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-5d13592516c7a4c6ba2f90669bf9b78b_l3.png)
Здесь: ![]() объем выборки,
объем выборки, ![]()
![]()
![]()
![]()
![]()
![]()
![]() — середины интервалов. Крайние незамкнутые интервалы заменены интервалами соответствующей длины.
— середины интервалов. Крайние незамкнутые интервалы заменены интервалами соответствующей длины.
![]()
![]()
Находим выборочную дисперсию:
![Rendered by QuickLaTeX.com \[ s^2 = \frac{1}{n}\sum_{i=1}^7{(x_i-\overline{x})^2\cdot n_i}. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-a207e9b5e8e5f076ad978afff64c0986_l3.png)
![]()
![]()
![]()
а) Находим границы, в которых с вероятностью 0,9946 заключено среднее время обслуживания всех клиентов пенсионного фонда.
По таблицам значений функции Лапласа находим ![]()
![]()
Интервальные оценки для средней находятся по формулам при объеме выборки ![]()
![]()
Искомые границы определяются двойным неравенством ![]() то есть
то есть ![]()
б) Находим среднюю квадратическую ошибку выборки для доли. С учетом того, что число клиентов очень велико, объем генеральной совокупности ![]() поэтому формула принимает вид (для бесповторной выборки):
поэтому формула принимает вид (для бесповторной выборки):
![]()
Здесь ![]() выборочная доля клиентов в выборке, время обслуживания которых составило меньше 6 минут:
выборочная доля клиентов в выборке, время обслуживания которых составило меньше 6 минут:
![]()
Тогда в нашем случае получаем:
![]()
Ищем вероятность того, что доля всех клиентов фонда с продолжительностью обслуживания менее 6 минут отличается от доли таких клиентов в выборке не более чем на 10% (по абсолютной величине).
![]()
в) Ищем объем повторной выборки, при котором с вероятностью 0,9907 можно утверждать, что доля всех клиентов фонда с продолжительностью обслуживания менее 6 минут отличается от доли таких клиентов в выборке не более чем на 10% (по абсолютной величине).
Учитывая, что ![]() по таблице значений функции Лапласа определяем, что
по таблице значений функции Лапласа определяем, что ![]() , предельная ошибка доли равна
, предельная ошибка доли равна ![]() , и объем повторной выборки равен:
, и объем повторной выборки равен:
![]()
Задача 2. По данным задачи 1, используя ![]() -критерий Пирсона, на уровне значимости a=0,05 проверить гипотезу о том, что случайная величина
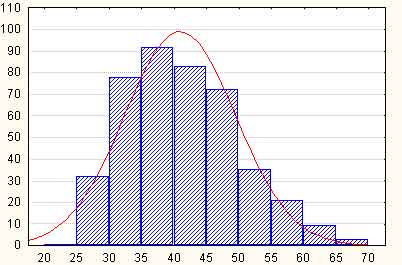
-критерий Пирсона, на уровне значимости a=0,05 проверить гипотезу о том, что случайная величина ![]() – время обслуживания клиентов – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
– время обслуживания клиентов – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
Решение. Нормальное распределение имеет вид:
![]()
Используем данные, полученные в предыдущем задании: ![]()
![]() Поскольку количество наблюдений достаточно велико, в качестве дисперсии нормального распределения
Поскольку количество наблюдений достаточно велико, в качестве дисперсии нормального распределения ![]() возьмем
возьмем ![]() То есть
То есть ![]()
![]()
![]() Тогда теоретическое нормальное распределение принимает вид:
Тогда теоретическое нормальное распределение принимает вид:
![]()
Для расчета вероятностей ![]() попадания случайной величины в интервал
попадания случайной величины в интервал ![]() используем функцию Лапласа:
используем функцию Лапласа:
![]()
![]()
Для нашего случая получаем:
![]()
![]()
Для каждого промежутка получаем:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Составим таблицу
| Интервал |
Эмпирические частоты |
Вероятности |
|
| <2 | 6 | 0,0365 | 1,513 |
| 2-4 | 10 | 0,1249 | 0,4964 |
| 4-6 | 21 | 0,25221 | 0,7064 |
| 6-8 | 39 | 0,2881 | 3,6042 |
| 8-10 | 15 | 0,19606 | 1,0821 |
| 10-12 | 6 | 0,0754 | 0,3145 |
| >12 | 3 | 0,017225 | 0,9475 |
| Сумма | 100 | 0,9904 |
Итого значение статистики ![]()
Определим количество степеней свободы по формуле ![]()
![]() — число интервалов,
— число интервалов, ![]() — число параметров закона распределения. То есть
— число параметров закона распределения. То есть ![]() Соответствующее критическое значение статистики для уровня значимости
Соответствующее критическое значение статистики для уровня значимости ![]() равно
равно ![]() , что больше полученных
, что больше полученных ![]() . Вывод: гипотеза подтверждается.
. Вывод: гипотеза подтверждается.
Тут бы надо построить графическое изображение эмпирического (в виде гистограммы) и теоретического (в виде линии) распределений. На бумаге я это сделал без труда, а вот на компьютере почему-то стало лень рисовать. Может быть найдутся желающие мне помочь улучшить статью? Something like that:
Задача 3. Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице:
| 5-9 | 9-13 | 13-17 | 17-21 | 21-25 | Итого | |
| 15-21 | 3 | 2 | 1 | 6 | ||
| 21-27 | 1 | 2 | 3 | 2 | 8 | |
| 27-33 | 2 | 7 | 3 | 12 | ||
| 33-39 | 2 | 5 | 8 | 15 | ||
| 39-45 | 2 | 2 | 1 | 5 | ||
| 45-51 | 2 | 2 | 4 | |||
| Итого | 4 | 8 | 18 | 17 | 3 | 50 |
Необходимо:
- вычислить групповые средние , построить эмпирические линии регрессии;
- предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
- найти уравнения прямых регрессии, дать экономическую интерпретацию полученных уравнений;
- вычислить коэффициент корреляции; на уровне значимости a=0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
- используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43 %.
Решение.
1. Находим групповые средние по формулам:
![]()
Здесь ![]() и
и ![]() — середины соответствующих интервалов:
— середины соответствующих интервалов:
![]()
![]()
Пример вычислений групповых средних:
![]()
![]()
Полученные значения заносим в таблицу:
| 7 | 11 | 15 | 19 | 23 | Групповые средние по Y | |
| 18 | 3 | 2 | 1 | 9,667 | ||
| 24 | 1 | 2 | 3 | 2 | 14 | |
| 30 | 2 | 7 | 3 | 15,333 | ||
| 36 | 2 | 5 | 8 | 16,6 | ||
| 42 | 2 | 2 | 1 | 18,2 | ||
| 48 | 2 | 2 | 21 | |||
| Групповые средние по X | 19,5 | 27 | 31,333 | 35,647 | 46 |
2. Отвечаем на оставшиеся вопросы.
a) Для нахождения уравнений регрессии вычисляем необходимые суммы:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Искомые линии регрессии тогда имеют вид:
![]()
![]()
б) Находим коэффициент корреляции ![]() радикал берем с плюсом, поскольку коэффициенты
радикал берем с плюсом, поскольку коэффициенты ![]() и
и ![]() положительны:
положительны:
![]()
Оцениваем коэффициент значимости корреляции:
![Rendered by QuickLaTeX.com \[ t=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}} = \frac{0,6696\sqrt{50-2}}{\sqrt{1-0,6696^2}} = 6,246. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-1c37cf546e1cc1e0ed87966a23c65b57_l3.png)
По таблице значений критерия Стьюдента для уровня значимости в ![]() находим
находим ![]() Так как
Так как ![]() коэффициент значимости значительно отличается от нуля, делаем вывод, что связь тесная и прямая.
коэффициент значимости значительно отличается от нуля, делаем вывод, что связь тесная и прямая.
в) По найденному уравнению регрессии оцениваем рост производительности труда при степени автоматизации производства 43 %:
![]() %.
%.
Репетитор по физике и математике
Сергей Валерьевич
© Марк Твен


СПАСИБО ОГРОМНЕЙШЕЕ!!!!!!
🙂 Пожалуйста, очень рад, что это кому-то пригодилось.
еще как)
подскажите пожалуйста, я не совсем понимаю, про данные которые надо заносить в таблицу. это надо новую табл. рисовать или в первую заносить значения???
нужно добавить в первую таблицу соответствующие столбики и строки и внести в них посчитанные значения групповых средних. Расписал для примера, как они считаются для одного интервала, для остальных аналогично.
1. Провести группировку, если известно, что студенты сдавали тест по русскому языку. Ими были получены следующие баллы:
91; 43; 55; 64; 71; 70; 52; 50; 92; 95; 44; 59; 69; 62; 102; 100; 48; 47; 49; 88.
Кристина, могу Вам посоветовать ознакомиться с этим материалом: http://www.aup.ru/books/m81/3.htm
Все очень доходчиво расписано, можно легко разобраться.
Огромное спасибо,все доходчиво написано!
я не могу правильно нарисовать чертёж,вы не могли бы мне с ним помочь?
Надо по горизонтальной оси отложить интервалы (для эмпирического распределения) или середины соответствующих интервалов (для теоретического разбиения), а по вертикальной соответственно эмпирические или теоретические вероятности.
Сергей, добрый вечер!
Подскажите пожалуйста, во второй задаче такие данные как ЭМПИРИЧЕСКИЕ ЧАСТОТЫ вы как посчитали?
Заранее спасибо)
Сергей,извините,что побеспокоила) я уже разобралась-это элементарно) видимо сильно устала) еще раз спасибо)
Всегда пожалуйста, даже если в данном случае не за что:-)
помогите решить
Вероятности того, что каждый из трех кассиров занят обслуживанием покупателей, равны соответственно 0,7; 0,8; 0,9.
Найти вероятность того, что в данный момент заняты обслуживанием покупателей:
а) все кассиры;
б) только один кассир;
в) хотя бы один кассир
1) И первый И второй И третий кассир заняты (И — логическое умножение): 0.7*0.8*0.9 = 0.504
2) (занят первый И НЕ занят второй И НЕ занят третий) ИЛИ (занят второй И НЕ занят первый И НЕ занят третий) ИЛИ (занят третий И НЕ занят первый И НЕ занят второй) (ИЛИ — логическое сложение, НЕ — логическое отрицание): 0.7*(1-0.8)*(1-0.9) + (1-0.7)*0.8*(1-0.9) + (1-0.7)*(1-0.8)*0.9 = 0.092
3) Ищем вероятность противоположного события (не занят ни один кассир). То есть НЕ занят первый И НЕ занят второй И НЕ занят третий: (1-0.7)*(1-0.8)*(1-0.9) = 0.006. Интересующее нас событие будет противоположным данному, поэтому его вероятность равна 1-0.006 = 0.994
Огромнейшее спасибо, это страница просто спасение для меня!!!)
Просто и гениально!!!!!!!!!! Выражаю огромную благодарность от непонимающих тервер!))
Спасибо! Рад, что Вам это пригодилось.
спасибо Вам огромное. Очень помогли!!!
Спасибо огромное!
Извините,но вы не правильно нашли выборочную дисперсию, поскольку (если вы внимательно посмотрите на формулу),то S^2=(100/99)*дисперсию=7,1 . (дисперсия в нашем случае равна 7,0284)
С уважением,Екатерина.
Честно говоря, я настолько давно это решал, что все благополучно забыл. Скорее всего Вы правы. Поясните только, пожалуйста, почему для вычисления выборочной дисперсии нужно домножать обычную дисперсию на 100/99?
во 2 задаче,буква Б, имеется ошибка при расчете средней квадратической ошибки выборки для доли..в формуле стоят скобки, однако при подсчете автор забыл их проставить… От сюда и потекла ошибка 🙂
Действительно, скобки там были пропущены, я исправил, но посчитано там всё было с учетом этих скобок.
Спасибо ОГРОМНОЕ!!! Вы облегчили жизнь бедным студентам!!! Побольше бы таких!!!
спасибо большое! очень помогли!
Поясните, пожалуйста, почему в задаче 1, пункт 3 delta взята равной 0.2651. Как это связано с тем, что спрашивается — долей клиентов с временем обслуживания менее 6 минут, отличающейся не более чем на 10% от таких же клиентов в выборке?
Честно говоря, это было так давно, что я уже не помню. Рекомендую Вам посмотреть вот здесь: http://mathprofi.com/uploads/files/63_f_41_kontrolnaya-po-terveru-i-statistike.pdf?key=610bbca7a69e2aceaa880a44d5738ad6
Поясните пожалуйста, откуда в 3 задаче 26070?
Нужно посчитать записанную двойную сумму и получится этот ответ.