Для получения высоких баллов за ЕГЭ по математике, гарантирующих поступление в престижные вузы, требуется умение решать достаточно сложные задачи. Но как научить ученика решать их в условиях современной школы, когда квалификация многих школьных учителей не позволяет им самим решать последние задания из ЕГЭ, не говоря уже о том, чтобы научить этому своих учеников? Традиционная классно-урочная форма обучения не способна дать ученику необходимых знаний и умений для сдачи ЕГЭ на уровне выше 70-80 баллов. Помочь здесь могут только занятия с репетитором.
Для решения этой задачи в преподавании я использую так называемую концепцию развивающего обучения, основные принципы которой были разработаны в середине XX в. выдающимися отечественными психологами Д. Б. Элькониным и В. В. Давыдовым. В частности, согласно этой концепции постепенное усложнение учебного материала должно находиться в так называемой зоне ближайшего развития. Л. С. Выготский определил эту зону содержанием таких задач, которые ученик может решить лишь с помощью преподавателя, но после приобретения опыта совместной деятельности он становится способным к самостоятельному решению аналогичных задач.
В соответствии с данным подходом на своих занятиях я использую один весьма эффективный методический прием, основанный на том, что очень многие задачи, будь то сложные или простые, часто решаются одним и тем же способом (к примеру, выполнением типичного дополнительного построения, стандартной заменой при решении уравнений и т. п.). Знание этого способа порой делает даже очень сложную задачу посильной почти каждому ученику. Рассмотрим для примера несколько геометрических задач, каждая их которых легко решается с помощью одного и того же дополнительного построения: проведения прямой, параллельной одной из сторон данного треугольника.
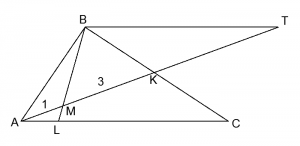
Задача 1. На медиане AK треугольника ABC взята точка M, причем AM : MK = 1 : 3. В каком отношении прямая BM делит сторону AC?
Решение:
Через вершину B проведем прямую, параллельную AC, продлим медиану AK до пересечения с этой прямой в точке T. Из равенства треугольников KBT и AKC (по стороне и двум прилежащим углам: BK = KC, т. к. AK — медиана, ∠BKT = ∠AKC — вертикальные, ∠KBT = ∠KCA — накрест лежащие при параллельных прямых AC, BT и секущей BC) следует, что BT = AC и AK = KT.
Из подобия треугольников AML и MBT (по двум углам: ∠MAL = ∠BTK, ∠ALB = ∠LBT — накрест лежащие при параллельных прямых AC, BT и секущих BL, AT) следует, что AL : BT = AL : AC = AM : MT. Поскольку AK = KT, то AM : MT = 1 : 7. Тогда AL : AC = 1 : 7, а AL : LC = 1 : 6.
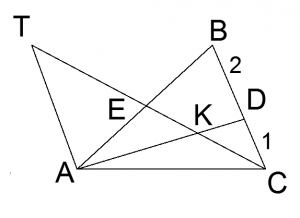
Задача 2. В треугольнике ABC биссектриса AD делит сторону BC в отношении BD : DC = 2 : 1. В каком отношении медиана CE делит эту биссектрису?
Решение:
Через вершину A проведем прямую, параллельную стороне BC, продлим медиану CE до пересечения с этой прямой в точке T. Треугольник TEA равен треугольнику EBC по стороне и двум прилежащим к ней углам (AE = EB, т. к. CE — медиана, ∠AET = ∠CEB — вертикальные, ∠TAB = ∠ABC — накрест лежащие при параллельных прямых TA, BC и секущей AB). Следовательно BC = TA и TA = 3DC.
Треугольники TKA и DKC подобны по двум углам (∠TAD = ∠KDC, ∠TCD = ∠ATC — накрест лежащие при параллельных прямых TA, BC и секущих AD, TC), следовательно KD : KA = DC : TA = 1 : 3.
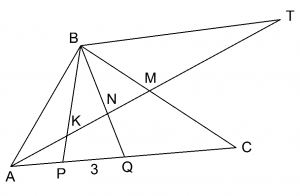
Задача 3. В треугольнике ABC на основании AC взяты точки P и Q так, что AP < AQ. Прямые BP и BQ делят медиану AM на три равные части. Известно, что PQ = 3. Найдите AC.
Решение:
Проведём через вершину B прямую, параллельную AC, и продолжим медиану AM до пересечения с этой прямой в точке T. Из равенства треугольников AMC и BMT (по стороне и двум прилежащим к ней углам: BM = MC, т. к. AM — медиана, ∠AMC = ∠BMT — вертикальные, ∠BTM = ∠MAC — накрест лежащие при параллельных прямых AC, BT и секущей AT) следует, что AC = BT и MT = AM. Тогда AK = 1/6 AT, AN = 1/3 AT.
Из подобия треугольников AKP и KBT (по двум углам: ∠TAP = ∠BTA, ∠APB = ∠TBP — накрест лежащие при параллельных прямых AC, BT и секущих AT, BP) следует, что AP = 1/5BT = 1/5AC, а из подобия треугольников ANQ и BNT: AQ = 1/2BT = 1/2AC. Поскольку AQ — AP = PQ = 3, то 1/2AC — 1/5AC = 3. Отсюда находим, что AC = 10.
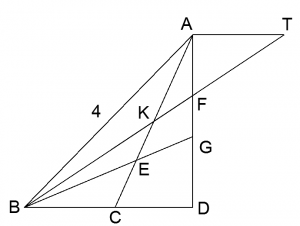
Задача 4. В треугольнике ABC проведена высота AD. Прямые, одна из которых содержит медиану BK, а вторая — биссектрису BE, делят эту высоту на три равных отрезка. Известно, что AB = 4. Найдите сторону AC.
Решение:
BE — биссектриса треугольника ABC, а потому BG — также биссектриса треугольника BDA. Из условия следует, что AG = 2GD, поэтому по свойству биссектрисы внутреннего угла треугольника AB = 2BD, следовательно BD = 2.
Через вершину A проведем прямую, параллельную стороне BC. Продлим медиану BK треугольника ABC до пересечения с этой прямой с точке T. Из равенства треугольников AKT и BKC (по стороне и двум прилежащим к ней углам: AK = KC, т. к. BK — медиана, ∠KBC = ∠ATK — вертикальные, ∠BCK = ∠KAT — накрест лежащие при параллельных прямых BC, AT и секущей AC) следует, что BC = AT.
Из подобия треугольников ATF и FBD (по двум углам: ∠ATF = ∠FBD — накрест лежащие при параллельных прямых BD, AT и секущей BT, ∠TAF = ∠BDF — прямые, коэффициент подобия AF : FD = 1 : 2) следует, что BD = 2AT, а значит AT = BC = CD = 1. Из теоремы Пифагора для треугольника ABD следует, что AD = 2√3. И из теоремы Пифагора для треугольника ACD окончательно следует, что AC = √13.
Вот так одно дополнительное построение помогло решить четыре задачи совершенно разного уровня сложности. Разобрав одно задание совместно с преподавателем, ученик обычно решает все остальные или по крайней мере проявляет при их решении большую самостоятельность.
Эффективность идей развивающего обучения доказана огромным опытом их использования в преподавании. Проблема в том, что традиционная классно-урочная форма не пригодна для реализации концепций такого обучения. Этот длительный и трудный процесс во всей полноте может быть осуществлен только в рамках систематических индивидуальных занятий под чутким руководством профессионального репетитора.
Репетитор по математике в Тропарёво
Сергей Валерьевич