В данной статье остановимся кратко на решении задач C1 из ЕГЭ по математике. Эти задания представляют собой уравнения, которые требуется, во-первых, решить (то есть найти их решения, причем все), во-вторых, осуществить отбор решений по тому или иному ограничению. В последние годы на ЕГЭ по математике в заданиях C1 школьникам предлагаются для решения тригонометрические уравнения, поэтому в данной статье разобраны только они. Примеры структурированы по методам решения уравнений, от самых элементарных, до достаточно сложных.
Прежде чем перейти к разбору конкретных тригонометрических уравнений, вспомним основные формулы тригонометрии. Приведем их здесь в справочном виде.
Решение простейших тригонометрических уравнений
![]()
принадлежащие промежутку ![]()
Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем ![]() (на всякий случай, эта запись означает, что числа
(на всякий случай, эта запись означает, что числа ![]() и
и ![]() принадлежат множеству целых чисел):
принадлежат множеству целых чисел):
![Rendered by QuickLaTeX.com \[ 4x+\frac{\pi}{4}=\pm\operatorname{arccos \left(-\frac{\sqrt{2}}{2}\right)}+2\pi k. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-600bd6daa90af5fa4124c683eb7663ac_l3.png)
Арккосинус ![]() есть число, заключенное в интервале от
есть число, заключенное в интервале от ![]() до
до ![]() , косинус которого равен
, косинус которого равен ![]() .
.
Арксинус ![]() есть число, заключенное в интервале от
есть число, заключенное в интервале от ![]() до
до ![]() , косинус которого равен
, косинус которого равен ![]() .
.
Другими словами, нам нужно подобрать такое число из промежутка ![]() косинус которого был бы равен
косинус которого был бы равен ![]() Это число
Это число ![]() Используя это, получаем:
Используя это, получаем:
![Rendered by QuickLaTeX.com \[ 4x+\frac{\pi}{4} = \pm\frac{3\pi}{4}+2\pi k\Leftrightarrow \left[\begin{array}{l}x = \frac{\pi}{8}+\frac{\pi k}{2}, \\ x = -\frac{\pi}{4}+\frac{\pi n}{2}.\end{array}\right. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4e1b7dcb8f1bb9b0ff44ee1900d0e206_l3.png)
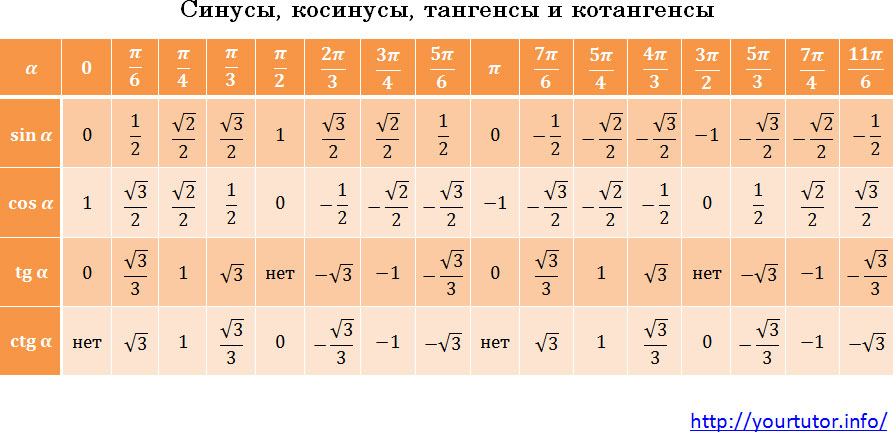
Вообще, значения тригонометрических функций от основных аргументов нужно знать. Их совсем чуть-чуть:
Хотя на самом деле запоминать их вовсе не обязательно. Существует очень простой алгоритм, используя который, можно в уме легко вычислять значения тригонометрических функций всех основных аргументов. Просто у каждого он свой. Придумайте его и для себя. Просто посмотрите на эту таблицу. Числа в ней расположены не случайным образом, определенная закономерность есть, постарайтесь ее найти.
Итак, вернемся к нашему заданию. Из полученных серий выбираем только те ответы, которые принадлежат промежутку ![]() Воспользуемся для этого методом двойных неравенств. Вы помните, что
Воспользуемся для этого методом двойных неравенств. Вы помните, что ![]() и
и ![]() — целые числа:
— целые числа:
1) ![]()
![]()
![]()
![]()
![]()
2) ![]()
![]()
![]()
![]()
![]()
Задача для самостоятельного решения №1. Найдите корни уравнения ![]() принадлежащие промежутку
принадлежащие промежутку ![]()
![]()
![]()
Решение линейных тригонометрических уравнений
![]()
принадлежащие промежутку ![]()
Решение. Подобные уравнения решаются один весьма интересным, на мой взгляд, способом. Разделим обе части на ![]() , уравнение тогда примет вид:
, уравнение тогда примет вид:
![]()
Подберем такое число, синус которого равен ![]() а косинус равен
а косинус равен ![]() Например, пусть это будет число
Например, пусть это будет число ![]() . С учетом этого перепишем уравнение в виде:
. С учетом этого перепишем уравнение в виде:
![]()
Присмотревшись, слева от знака равенства усматриваем разложение косинуса разности ![]() и
и ![]() Это и есть ключ к решению. Имеем:
Это и есть ключ к решению. Имеем:
![]()
![]()
Осуществляем отбор решений, входящих в промежуток ![]() :
:
1) ![]()
![]()
![]()
![]()
![]()
2) ![]()
![]()
![]()
![]()
![]()
Задача для самостоятельного решения №2. Найдите корни уравнения ![]() принадлежащие промежутку
принадлежащие промежутку ![]()
![]()
![]()
Решение тригонометрических уравнений методом замены переменной
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезке ![]()
Решение. Сразу оговорим ограничения, накладываемые на переменную ![]() в этом уравнении:
в этом уравнении: ![]() Откуда взялось это ограничение? Правильно, функция
Откуда взялось это ограничение? Правильно, функция ![]() не существует при этих значениях
не существует при этих значениях ![]() Используем замену переменной:
Используем замену переменной: ![]() Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
![]()
Переходим к обратной замене:
![]()
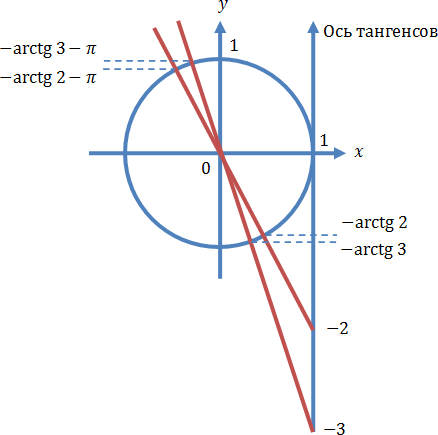
Осуществляем отбор решений. Проведем его на этот раз с использованием единичной окружности.
Из рисунка видно, что в интересующий нас промежуток входят только два значения из этих серий: ![]() Обратите внимание на один существенный момент. На рисунке точки
Обратите внимание на один существенный момент. На рисунке точки ![]() и
и ![]() принадлежат оси тангенсов, а точки
принадлежат оси тангенсов, а точки ![]()
![]()
![]() и
и ![]() — единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.
— единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.
Ответ: ![]()
Задача для самостоятельного решения №3. Дано уравнение ![]()
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![]()
![]()
![]()
Решение тригонометрических уравнений методом разложения на множители
![]()
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![]()
Решение. Равносильными преобразования приводим уравнение к виду:
![]()
![]()
![]()
![]()
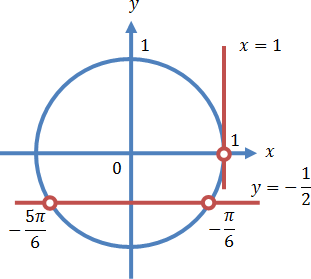
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\cos x=1, \\ \sin x=-\frac{1}{2} \end{array}\right.\Leftrightarrow\left[\begin{array}{l}x=2\pi k, \\ x=-\frac{\pi}{6}+2\pi n, \\ x=-\frac{5\pi}{6}+2\pi z.\end{array}\right. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c0ac3379edc46ce1bf97df0f46a830ac_l3.png)
Осуществляем отбор решений с помощью единичной окружности.
Из рисунка видно, что в интересующий нас промежуток входят только два значения из всех этих серий: ![]()
Задача для самостоятельного решения №4. Дано уравнение
![]()
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![]()
![]()
![]()
Комбинированные уравнения
При решении уравнений этого типа важно обращать внимание на область допустимых значений входящих в него переменных. Именно поэтому составители вариантов ЕГЭ не просят учеников осуществлять отбор решений из полученных серий ответов. Решение этих уравнений само собой подразумевает выполнение данной математической операции.
![]()
Решение. Данное уравнение эквивалентно следующей системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}1-2\sin 3x\sin 7x=\cos 10x, \\ \cos 10x\geqslant 0.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-5e7804c5a3444eda3706d8c6a9cc8bc0_l3.png)
Обратите внимание! Писать, что ![]() нет никакой необходимости, поскольку по условию это выражение равно выражению
нет никакой необходимости, поскольку по условию это выражение равно выражению ![]() которое, в свою очередь, больше или равно нулю.
которое, в свою очередь, больше или равно нулю.
Решаем первое уравнение системы:
![]()
![]()
![]()
![]()
Нужно, чтобы ![]() поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только
поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только ![]()
Ответ: ![]()
Задача для самостоятельного решения №5. Решите уравнение: ![]()
![Rendered by QuickLaTeX.com \[ \frac{2\sin^2 x-\sin\left(\frac{3\pi}{2}+x\right)-1}{\sqrt{\sin x}}=0. \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-b29f83ad79819cdf0623a3f50f53cbf1_l3.png)
Решение. Данное уравение равносильно системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}2\sin^2 x-\sin\left(\frac{3\pi}{2}+x\right)-1=0, \\ \sin x>0\end{cases}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-9796d3e88520ad252eea21fb51f21987_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}2\cos^2 x-\cos x-1=0,\\ \sin x>0\end{cases}\Leftrightarrow \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-dbab64445b6b27423f4c9a5b3a45e710_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}\left[\begin{array}{l}\cos x = 1, \\ \cos x =-\frac{1}{2},\end{array} \\ \sin x >0\right.\end{cases}\Leftrightarrow \begin{cases}\left[\begin{array}{l}x=2\pi k, \\ x=\pm\frac{2\pi}{3}+2\pi n,\end{array} \\ \sin x >0\right.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-20bc473770ab6419cd1a45ba72b7178f_l3.png)
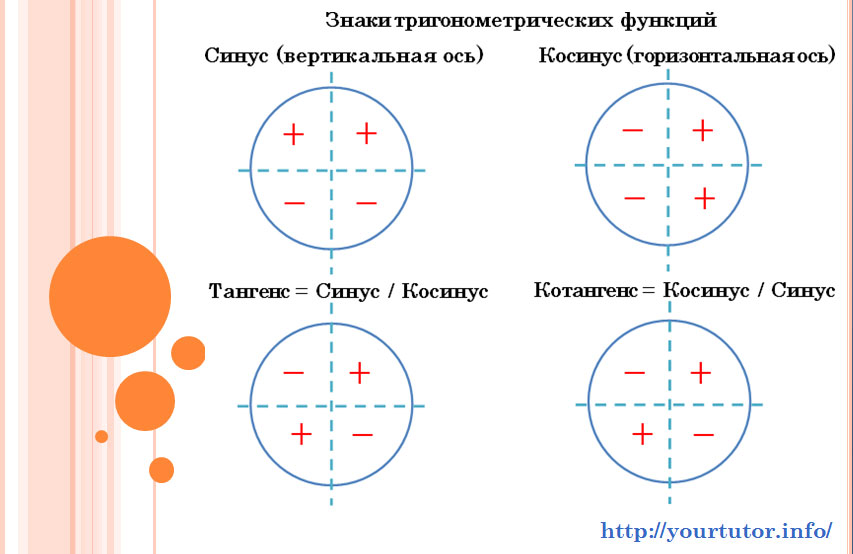
Тригонометрическая функция синус положительна в первой и второй координатной четвертях, поэтому из полученных серий выбираем только эту: ![]()
Раз уж мы с этим столкнулись, не лишним будет повторить, какие знаки принимают тригонометрические функций в различных координатных четвертях:
Ответ: ![]()
Задача для самостоятельного решения №6. Решите уравнение: ![]()
![]()
Решение. Область допустимых значения уравнения определяется условием: ![]() то есть
то есть ![]() Разобьем решение на два случая:
Разобьем решение на два случая:
1) Пусть ![]() тогда уравнение принимает вид:
тогда уравнение принимает вид:
![]()
![]()
Последнее равенство неверно, поэтому в данном случае решений у уравнения не будет.
2) Пусть ![]() тогда уравнение принимает вид:
тогда уравнение принимает вид:
![]()
![]()
Условию ![]() удовлетворяет только последняя серия.
удовлетворяет только последняя серия.
Ответ: ![]()
Задача для самостоятельного решения №7. Решите уравнение: ![]()
ЕГЭ по математике 2012 позади, все в ожидании результатов, которые обещали объявить во вторник 19 июня. Сейчас уже поздно желать высоких баллов на экзаменах нынешним выпускникам. Но вот пожелать успехов сегодняшним десятиклассникам я возможности не упущу. Удачи вам в подготовке и помните, что чем раньше она начнется, тем лучше будут результаты на экзамене.
Репетитор математики
Сергей Валерьевич
P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.





Здравствуйте. Не могли бы помочь:
sin x+2cos2x=3/2
Заранее спасибо!
Здравствуйте, нужно использовать формулу двойного угла для косинуса:
sinx+2(1-2sin^2x)=3/2
sinx+2-4sin^2x=3/2
8sin^2x-2sinx-1=0
Подстановка sinx = t
8t^2-2t-1=0
То есть t = 1/2 или t=-1/4
Обратная подстановка: sinx = 1/2 или sinx = -1/4.
Откуда получаем: x = pi/6+2pi*n, 5pi/6+2pi*n, -arcsin(1/4)+2pi*n, pi+arcsin(1/4)+2pi*n.
Здравствуйте мне нужна ваша помощь
Огромное спасибо!!!!!
Очень вам благодарен! Но не могли бы еще помочь, нужно доказать тождество.
2sin2a+sin4a / 2(cosa+cos3a)= tg2a*cosa
Рад был помочь. Что касается тождества. Упрощаем числитель: 2sin2a+sin4a = (формула синуса двойного угла) = 2sin2a+2sin2acos2a = 2sin2a(1+cos2a). Теперь упрощаем знаменатель: 2(cosa+cos3a) = (формула сумма косинусов) = 2*2cos2acosa. Теперь делим одно на другое: 2sin2a(1+cos2a)/(2*2cos2acosa) = tg2a(1+cos2a)/(cosa) = (формула косинуса двойного угла) = tg2a(1+2cos^2a-1)/(cosa) = tg2a*cosa.
Здравствуйте, не могли бы вы помочь!
cos(3x+pi/4)=-√3/2
Здравствуйте,
cos(3x+pi/4)=-√3/2
3x+pi/4 = +-5pi/6+2pi*k
3x = 7pi/12+2pi*n или 3x = -13pi/12+2pi*k
x = 7pi/36+2pi*n/3 или x = -13pi/36+2pi*k/3
Еще рас Спасибо))))
Добрый вечер! Помогите пожалуйста: tg x=3\2. Чему равен х?
Здравствуйте, x = arctg(3/2)+pi*n
спасибо огромное)
Здравствуйте, нужна подсказка:
2sin^2(x) + cos(4x)=0 решая эту ересь, получил, что
sin(x)=sqrt(2)/2, где X1= pi/4 + 2pi*n; X2=3pi/4 + 2pi*k;
И найти нужно корни, удовлетворяющие условию:
|x|<3/2, т.е x∈(-3/2;3/2)
сейчас вот биквадрат получился 8sin^4(x)-6sin^2(x) +1=0; я вообще могу записать, что
cos^2(2x)=1-sin^2(2x)? могу ведь
Там sin(x)= +-sqrt(2)/2 и sin(x) = +-1/2; и в интервал: (-1.5;1.5) попадает только x= +-pi/4 и x= +-pi/6, вроде так.
Здравствуйте.
Формула понижения степени:
sin^2(x) = (1-cos(2x))/2. Тогда получаем:
1-cos(2x)+cos(4x) = 0.
Далее формула двойного косинуса: cos(4x) = 2cos^2(2x)-1. Получаем:
2cos^2(2x)-cos(2x)=0
cos(2x)(2cos(2x)-1) = 0
cos(2x)=0 или cos(2x)=1/2
x = pi/4+pi*k/2 или x = +-pi/6+pi*k
На интервале (-1.5;1.5) это -pi/4, -pi/6, pi/6 и pi/4
надо запомнить формулу, спасибо)
y=4 /(2 cosx-1)
найдите область определения
Все числа, кроме x = +-pi/3+2pi*n. При этих значениях знаменатель равен 0, чего быть не должно.
Здравствуйте, помогите пожалуйста . решить уравнение sin x/2 =корень из 2 делить на 2
Здравствуйте, sin x/2 =корень из 2 делить на 2, значит x/2 = pi/4+2pi*n и x/2 = 3pi/4+2pi*n. Откуда x = pi/8+pi*n и x = 3pi/8+pi*n.
решите пожалуйста, arccos (- корень из 3/2)
Ответ: 5pi/6
Здравствуйте, помогите пожалуйста решить уравнение: 6sin^2x + sin2x = 4
Здравствуйте. Посмотрите пример 4, там аналогичное уравнение рассмотрено.
Спасибо!
Здравствуйте, помогите пожалуйста вспомнить как решается cos (7pi)/12?
Здравствуйте. Начните с использования формулы понижения степени для косинуса.
Добрый день, подскажите пожалуйста.
при решении тригонометрического уравнения произвожу упрощение: 2sin^2 (3pi/2+x) получаю 2cos^2x или (минус) — 2cos^2x? (^2 это синус в квадрате). Мне кажется все-таки без минуса, но я не уверена…
Здравствуйте, да, без минуса, конечно. Потому что в синус в квадрате.
Добрый вечер, можете помочь?
y=(3x^2+4)*(5x^3-3)
Добрый вечер, это не тригонометрическое уравнение. А какое задание?
Да, это одно из возможных решений. Не факт, что самое оптимальное, но ответ получается верный.
Нет, косинус в числителе нужно взять по модулю.
Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.
Добрый вечер! Можете мне объяснить: при решении тригонометрического ур-я получаю ответ х= ( Pi/3) * (-1)^n + (Pi/3) + Pi*n. Но в решебнике приводятся ответы x=( 2Pi/3) + 2Pi*n и x= Pi + 2Pi*n, как так получается?
sin^4x+cos^4x+2sin^2xcos^2x х=π/12
помогите решить
Помогите решить системы
sin x+cos y=1
sin^2x+cos^2y=3/2
sin x+cos y=0
cos^2x+sin^2y=1/5
x-y=Pi
cos x-cos y=корень из 3
Помогите решить)
1)решите уравнение:
2cos(x+pi/6)=√3.
2)Найдите корни уравнения:
2cosx-cos²x=0.
Указать сумму корней sin(пx)=1,принадлежащих промежутку(1;6).
Здравствуйте, помогите найти действительный корень уравнения(((((( sin(x/4)+1-(1/x²) = 0
Помогите пожалуйста решить!!)
Решите уравнение √3 — ctgx=0 на промежутке [0;п/2]. Ответ записать в градусах.
Помогите, пожалуйста, решить!!!!
sin(x) + sin(2x +pi/6) = sqrt(3) * sin(2x) +1
Здравствуйте, можете подсказать каким методом надо решать уравнение cos(pi * x) + x^2 — 6x + 10 = 0?
Здравствуйте, x^2 — 6x + 10>=1, а -1<=cos(pi * x)<=1. Значит, нулю их сумма может быть только при таком значении x, когда x^2 — 6x + 10=1, а cos(pi * x)=-1. Это число 3.
Графически
Здравствуйте, потому что sin(2x) = 2sin(x)*cos(x), а знак выражения sin(x)*cos(x) совпадает со знаком выражения sin(x)/cos(x).
Помогите , пожалуйста, с заданием !
при каких значениях параметра а уравнение cos^x+(2a+3) sinx-a^2 = 0 имеет три корння на промежутке (0; 2п)
Добрый день!
В каких случаях пишут в конце разные буквы (и 2Пn, и 2Пк) ? Ведь при объединении решений этого будет некорректно?
Будет ли ошибкой на ЕГЭ, если я всё время буду писать скажем 2Пк ?
С уважением, Сергей.
Добрый день. Всё зависит от конкретной ситуации. Если Вы приведёте пример задания, в котором возникла спорная ситуация, тогда можно будет поговорить более предметно.
Добрый вечер, а подскажите пожалуйста, как решить это уравнение?
8sin*(П/6)-2 = 14-16cos(в квадрате)*(П-6)
П — это пи
Помогите плиз.
Постройке график функции y=2cos x+1
Помогите решить уравнение, пожалуйста!
y(x)=5sin(x/2)-3cos(1/2(x-Pi/3))
(sin pi/3 — 2 cos pi/2 + tg 11pi/6)tg(-pi/4)(sin 7pi/6 — 5 ctg 3pi/2 — tg 3pi/4 * tg(- 2pi/3) подскажите пожалуйста как решить
Здравствуйте. Помогите найти множествозначений функции
y=2-cos^2x
Здравствуйте, не могу найти область определения у функции у=sqrt(sin(x+П/4))
Помогите пожалуйста
Известно что sinx=-0,6; n<x<3n/2
Найти значения а) cos x б) sin2x
Здравствуйте, помогите пожалуйста:
tg(2п-х)cos(3п/2+2х)=sin(-п/2)
существует ли угол х при котором выполняется тоджества sin cosx=cos sinx
корни данного уравнения:
1−tgx/1+tgx=√ 3
находящиеся в промежутке значений: x∈[−π;2π]
1. Сколько всего таких корней :
2. Наименьший корень: x=
3. Наибольший корень: x=
Здравствуйте. Помогите решить уравнение sin x умножить на Пи\4 = корень из 2\2
Здравствуйте, помогите пожалуйста решить уравнение:
2*sin^2(3x)-sin(x)+cos(2x)=0
буду примного благодарна
Решите пожалуйста
Корень из 1-cosx+кореньcos (x/2+пи/2)=корень из 2
Здравствуйте, помогите решить уравнение cos3xcosx+sin3xsinx=1
Здравствуйте! Помогите решить уравнение sin2х +2sin^2х =0
и найти все корни этого уравнения, принадлежащие отрезку
[-2π; -π/2].
Помогите мне пожалуйста с решением уравнения:
Cos^2(2t+π\6)=1/2
Здравствуйте. Помогите мне пожалуйста с решением уравнения:
Cos^2(2t+π\6)=1/2
Здраствуйте. Помогите пожалуйста решить уравнение sin^2(x) + 2sin(x) × cos(x)= 3cos^2 (x)
Помогите решить
2cos^2x-1=0 на инетравле [-3p/2;3p/2]
(cos(11π/12)-cos(π/12))/sin(5π/12)
подскажите как это решить. с росписью действий. а чего то я запутался
здрасте где круг