При решении задач по геометрии из ЕГЭ и ОГЭ по математике довольно часто возникает необходимость, зная две стороны треугольника и угол между ними, найти третью сторону. Или же, зная все стороны треугольника, найти его углы. Для решение этих задач вам потребуется значение теоремы косинусов для треугольника. В данной статье репетитор по математике и физике рассказывает о том, как формулируется, доказывается и применяется на практике при решении задач данная теорема.
Формулировка теоремы косинусов для треугольника
Теорема косинусов для треугольника связывает две стороны треугольника и угол между ними со стороной, лежащей против этого угла. К примеру, обозначим буквами ![]() ,
, ![]() и
и ![]() длины сторон треугольника ABC, лежащие соответственно против углов A, B и C.
длины сторон треугольника ABC, лежащие соответственно против углов A, B и C.
Тогда имеет теорема косинусов для этого треугольника может быть записана в виде:
![]()
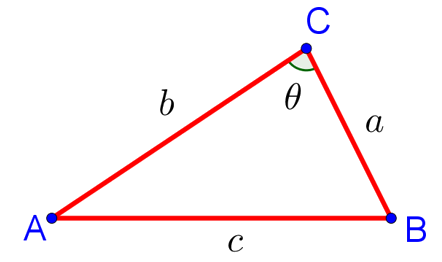
На рисунке для удобства дальнейших рассуждений угол С обозначен углом ![]() . Словами это можно сформулировать следующим образом: «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.»
. Словами это можно сформулировать следующим образом: «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.»
Понятно, что если бы вы выражали другую сторону треугольника, например, сторону ![]() , то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны
, то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны ![]() и
и ![]() . Выражение для квадрата стороны
. Выражение для квадрата стороны ![]() получается аналогично:
получается аналогично:
![]()
![]()
Доказательство теоремы косинусов для треугольника
Доказательство теоремы косинусов для треугольника проводят обычно следующим образом. Разбивают исходный треугольник на два прямоугольных треугольника высотой, а дальше играются со сторонами полученных треугольников и теоремой Пифагора. В результате после долгих нудных преобразований получаю нужный результат. Мне лично этот подход не по душе. И не только из-за громоздких вычислений, но ещё и потому что в этом случае приходится отдельно рассматривать случай, когда треугольник является тупоугольным. Слишком много трудностей.
Я предлагаю доказать эту теорему с помощью понятия «скалярного произведения векторов». Я сознательно иду на этот риск для себя, зная, что многие школьники предпочитают обходить эту тему стороной, считая, что она какая-то мутная и с ней лучше не иметь дела. Но нежелание возиться отдельно с тупоугольным треугольником во мне всё же пересиливает. Тем более, что доказательство в результате получается удивительно простым и запоминающимся. Сейчас вы в этом убедитесь.
Заменим стороны нашего треугольника следующими векторами:
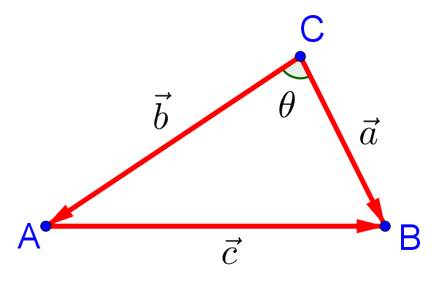
Согласно правилам сложения векторов имеем: ![]() . Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим
. Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим ![]() в правую часть равенства с противоположным знаком, в результате чего получаем следующее векторное выражение:
в правую часть равенства с противоположным знаком, в результате чего получаем следующее векторное выражение: ![]() .
.
Теперь возьмём скалярный квадрат обеих частей полученного выражения. В результате чего получим:
![]()
Я напоминаю, что по определению скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними. Из этого определения также следует, что скалярный квадрат вектора равен квадрату его длины. Действительно, ведь угол между вектором и им же самим равен нулю, то есть соответствующих косинус равен 1. То есть остаётся только квадрат длины вектора. Исходя из этого мы сразу получаем выражение для теоремы косинусов:
![]()
Что и требовалось доказать. Причём данное доказательство хорошо ещё тем, что позволяет лучше запомнить саму формулу. Ведь теперь становится понятным, откуда берётся этот хвост ![]() . Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол
. Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол ![]() может быть острым, тупым или прямым. И не требуется рассматривать доказательство для каждого из этих случаев, что не может не радовать.
может быть острым, тупым или прямым. И не требуется рассматривать доказательство для каждого из этих случаев, что не может не радовать.
Кстати, в случае, когда угол ![]() прямой, мы получаем
прямой, мы получаем ![]() , и выражение принимает следующий вид:
, и выражение принимает следующий вид: ![]() . Что мы получили? Правильно! Это запись теоремы Пифагора. Квадрат гипотенузы равен сумме квадратов катетов. Так что ниточки постепенно сплетаются. То есть, как обычно говорят, теорема косинусов для треугольника есть обобщение теоремы Пифагора на случай произвольного треугольника, не обязательно прямоугольного.
. Что мы получили? Правильно! Это запись теоремы Пифагора. Квадрат гипотенузы равен сумме квадратов катетов. Так что ниточки постепенно сплетаются. То есть, как обычно говорят, теорема косинусов для треугольника есть обобщение теоремы Пифагора на случай произвольного треугольника, не обязательно прямоугольного.
Примеры решения задач с использованием теоремы косинусов для треугольника
Надо сказать, что даже если вы не поняли приведённое выше доказательство, это не страшно, если ваша цель состоит в сдаче ЕГЭ или ОГЭ по математике. Специфика этих экзаменов состоит в том, что само доказательство теоремы косинусов у вас никто на них не спросит. Эти экзамены фактически вообще не проверяют знание теоретического материла из школьного курса математики. Важно лишь, чтобы вы знали, как эта теорема формулируется и умели применять её на практике для решения задач.
Используя теорему косинусов для треугольника, можно найти третью сторону, зная две стороны треугольника и угол между ними. Или же, зная длины всех сторон треугольника, найти величину всех его углов. Рассмотрим на примерах, как это делается.
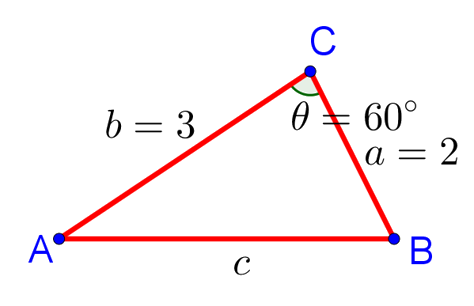
| Пример 1. В треугольнике ABC сторона AC равна 3, сторона CB равна 2, а угол C равен 60°. Найдите длину стороны AB. |
Используем теорему косинусов для треугольника ABC. Квадрат стороны ![]() равен сумме квадратов сторон
равен сумме квадратов сторон ![]() и
и ![]() за вычетом удвоенного произведения этих сторон на косинус угла между ними:
за вычетом удвоенного произведения этих сторон на косинус угла между ними:
![]()
Поскольку ![]() , то в результат получаем:
, то в результат получаем:
![]()
Значит, ![]() . Понятно, что отрицательное решение мы не берём, потому что длина отрезка — это число положительное.
. Понятно, что отрицательное решение мы не берём, потому что длина отрезка — это число положительное.
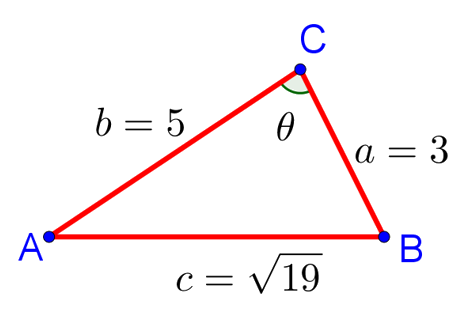
| Пример 2. В треугольнике ABC сторона AB равна |
Искомый угол на рисунке обозначен ![]() . Вновь запишем теорему косинусов для треугольника ABC. Поскольку все обозначения у нас сохранились, то и формула, выражающая теорему косинусов для этого треугольника, останется прежней:
. Вновь запишем теорему косинусов для треугольника ABC. Поскольку все обозначения у нас сохранились, то и формула, выражающая теорему косинусов для этого треугольника, останется прежней:
![]()
Подставим теперь в эту формулу все величины, которые даны. В результате получаем следующее выражение:
![]()
После всех вычислений и преобразований получаем следующее простое выражение:
![]()
Какой должна быть величина острого угла ![]() , чтобы его косинус был равен
, чтобы его косинус был равен ![]() Смотрим в таблицу, которую можно найти в этой статье, и получаем ответ:
Смотрим в таблицу, которую можно найти в этой статье, и получаем ответ: ![]() .
.
Вот так решаются задачи по геометрии с использованием теоремы косинусов для треугольника. Если вы собираетесь сдавать ОГЭ или ЕГЭ по математике, то этот материал вам нужно освоить обязательно. Соответствующие задачи почти наверняка будут на экзамене. Потренируйтесь самостоятельно в их решении. Выполните следующие задания:
- В треугольнике ABC сторона AB равна 4 см, сторона BC равна 6 см, угол B равен 30°. Найдите сторону AC.
- В треугольнике ABC сторона AB равна 10, сторона BC равна 8, сторона AC равна 9. Найдите косинус угла A.
Свои ответы и варианты решения пишите в комментариях. Удачи вам!
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич

Спасибо. Все понятно и доступно.
Спасибо большое