Рассмотрим классическую задачу. Дан куб, рёбра которого представляют собой проводники с каким-то одинаковым сопротивлением. Этот куб включается в электрическую цепь между всевозможными его точками. Вопрос: чему равно сопротивление куба в каждом из этих случаев? В данной статье репетитор по физике и математике рассказывает о том, как решается эта классическая задача. Присутствует также видеоурок, в котором вы найдёте не только подробное объяснение решения задачи, но и реальную физическую демонстрацию, подтверждающую все вычисления.
Итак, куб может быть включен в цепь тремя различными способами.
Сопротивление куба между противоположными вершинами
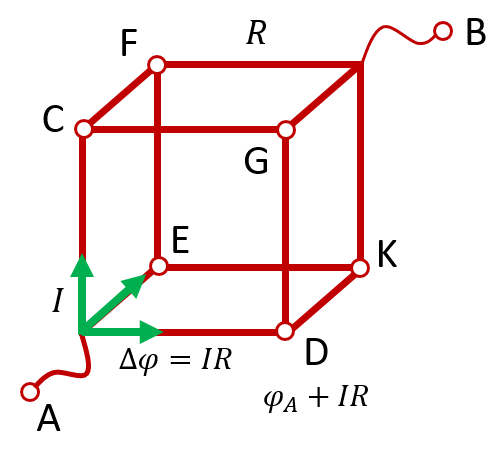
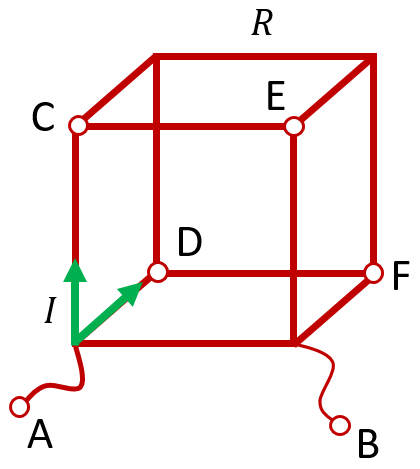
В этом случае ток, дойдя до точки A, распределяется между тремя рёбрами куба. При этом, поскольку все три ребра эквивалентны с точки зрения симметрии, ни одному из рёбер нельзя придать большую или меньшую «значимость». Поэтому ток между этими рёбрами должен распределиться обязательно поровну. То есть сила тока в каждом ребре равна ![]() :
:
В результате получается, что падение напряжения на каждом из этих трёх рёбер одинаково и равно ![]() , где
, где ![]() — сопротивление каждого ребра. Но падение напряжение между двумя точками равно разности потенциалов между этими точками. То есть потенциалы точек C, D и E одинаковы и равены
— сопротивление каждого ребра. Но падение напряжение между двумя точками равно разности потенциалов между этими точками. То есть потенциалы точек C, D и E одинаковы и равены ![]() . Из соображений симметрии потенциалы точек F, G и K также одинаковы.
. Из соображений симметрии потенциалы точек F, G и K также одинаковы.
Точки с одинаковым потенциалом можно соединять проводниками. Это ничего не изменит, потому что по этим проводникам всё равно не потечёт никакой ток:
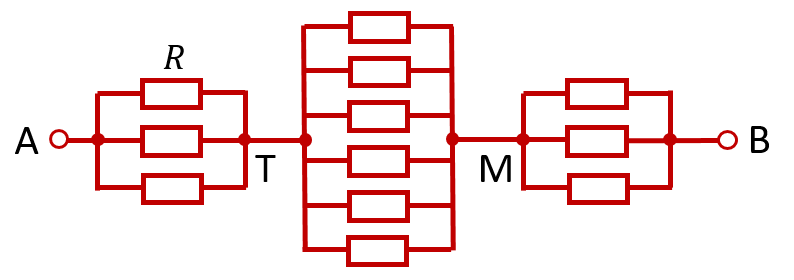
В результате получим, что рёбра AC, AD и AE соединятся в одной точке. Назовём её точкой T. Точно также рёбра FB, GB и KB соединятся в одной точке. Назовём её точкой M. Что касается оставшихся 6 рёбер, то все их «начала» окажутся соединены в точке T, а все концы — в точке M. В результате мы получим следующую эквивалентную схему:
Посчитать сопротивление такой схемы уже не составляет труда:
![]()
Сопротивление куба между противолежащими углами одной грани
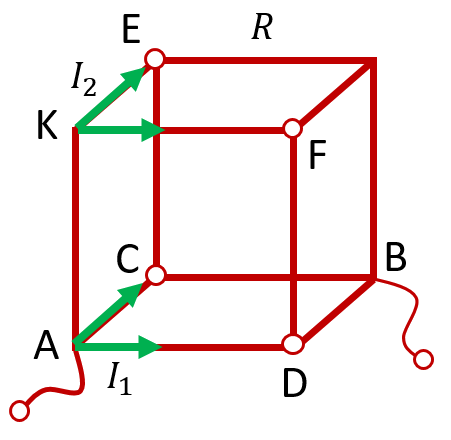
В данном случае эквивалентными являются рёбра AD и AC. По ним потечёт одинаковый ток ![]() . Кроме того, эквивалентными также являются KE и KF. По ним потечёт одинаковый ток
. Кроме того, эквивалентными также являются KE и KF. По ним потечёт одинаковый ток ![]() . Ещё раз повторим, что ток между эквивалентными рёбрами должен распределиться поровну, в противном случае нарушится симметрия:
. Ещё раз повторим, что ток между эквивалентными рёбрами должен распределиться поровну, в противном случае нарушится симметрия:
Таким образом, в данном случае одинаковым потенциалом обладают точки C и D, а также точки E и F. Значит эти точки можно объединить. Пусть точки C и D объединятся в точке M, а точки E и F — в точке T. Тогда получится следующая эквивалентная схема:
На вертикальном участке (непосредственно между точками T и M) ток не течёт. Действительно, ситуация аналогична уравновешенному измерительному мосту. Это означает, что данной звено можно исключить из цепи. После этого посчитать общее сопротивление не составит труда:
Сопротивление верхнего звена равно ![]() , нижнего —
, нижнего — ![]() . Тогда общее сопротивление равно:
. Тогда общее сопротивление равно:
![]()
Сопротивление куба между прилежащими вершинами одной грани
Это последний возможный вариант подключения куба в электрическую цепь. В этом случае эквивалентными рёбрами, через которые будет течь одинаковый ток, являются рёбра AC и AD. И, соответственно, одинаковые потенциалы будут иметь точки C и D, а также симметричные им точки E и F:
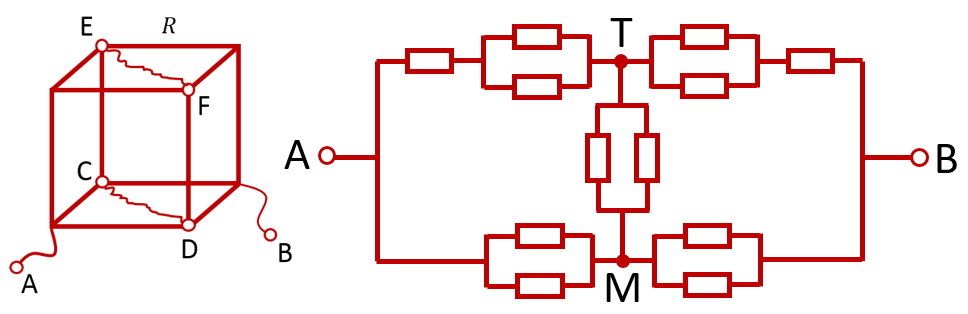
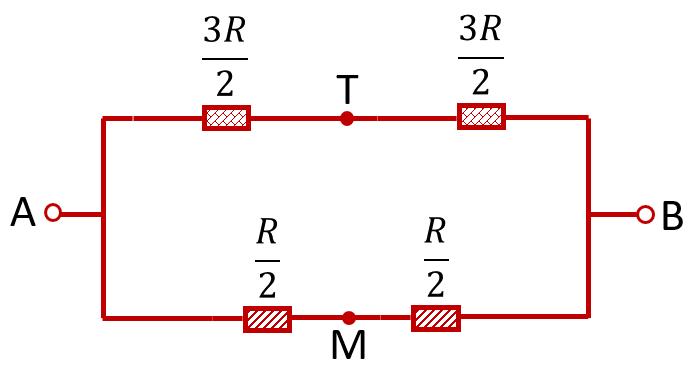
Вновь соединяем попарно точки с одинаковыми потенциалами. Мы можем это сделать, потому что ток между этими точками не потечёт, даже если соединить их проводником. Пусть точки C и D объединятся в точку T, а точки E и F — в точку M. Тогда можно нарисовать следующую эквивалентную схему:
Общее сопротивление полученной схемы рассчитывается стандартными способами. Каждый сегмент из двух параллельно соединённых резисторов заменяем на резистор сопротивлением ![]() . Тогда сопротивление «верхнего» сегмента, состоящего из последовательно соединённых резисторов
. Тогда сопротивление «верхнего» сегмента, состоящего из последовательно соединённых резисторов ![]() ,
, ![]() и
и ![]() , равно
, равно ![]() .
.
Этот сегмент соединён со «средним» сегментом, состоящим из одного резистора сопротивлением ![]() , параллельно. Сопротивление цепи, состоящей из двух параллельно соединённых резисторов сопротивлением
, параллельно. Сопротивление цепи, состоящей из двух параллельно соединённых резисторов сопротивлением ![]() и
и ![]() , равно:
, равно:
![]()
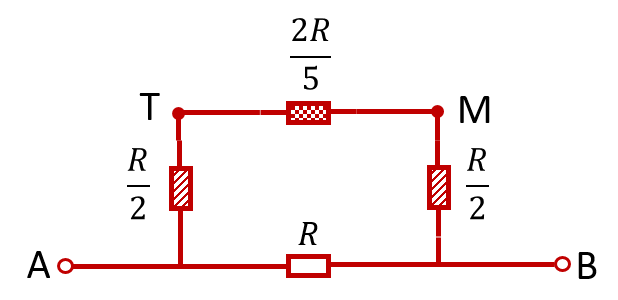
То есть схема упрощается до ещё более простого вида:
Как видно, сопротивление «верхнего» П-образного сегмента равно:
![]()
Ну а общее сопротивление двух параллельно соединённых резисторов сопротивлением ![]() и
и ![]() равно:
равно:
![]()
Эксперимент на измерению сопротивления куба
Чтобы показать, что всё это не математический трюк и что за всеми этими вычислениями стоит реальная физика, я решил провести прямой физической эксперимент по измерению сопротивления куба. Вы можете посмотреть этот эксперимент в видео, которые находится в начале статьи. Здесь я размещу фотографии экспериментальной установки.
Специально для этого эксперимента я спаял куб, рёбрами которого являются одинаковые резисторы. Также у меня есть мультиметр, который я включил в режиме измерения сопротивления. Сопротивление одиночного резистора равно 38.3 кОм:
Теперь смотрим сопротивление куба при различных его подключениях:
1) При подключении между диаметрально противоположным граням сопротивление равно 32.3 кОм:
Расчётное значение равно ![]() кОм.
кОм.
2) При подключении между соседним вершинам одной грани измеренное значение сопротивления равно 22.6 кОм:
Расчётное значение составляет ![]() кОм.
кОм.
3) При подключении между противоположным вершинам одной грани сопротивление равно 28.9 кОм:
Расчётное значение равно ![]() кОм.
кОм.
Как видите, мы получили очень хорошее согласование экспериментальных данных с результатам наших расчётов. Ошибка находится на уровне 1%. Погрешность измерений есть всегда. Это нормально. В данном случае эта погрешность связана, скорее всего, с тем, что сопротивление резисторов не строго 38.3 кОм, а может немного варьироваться.
Материал подготовил репетитор по физике и математике, Сергей Валерьевич
Если вам понравилась статья, смотрите также:







Очень наглядно, лаконично и понятно. Большое спасибо. Просто супер.
Да
Сергей Валерьевич, спасибо за такое прекрасное объяснение. Я очень долго искала именно такой вариант объяснения.
Рад, что статья оказалась для вас полезной.
Круто, спасибо, Сергей Валерьевич!
особенно замечательно, что показано экспериментальное подтверждение. спасибо.
В последнем варианте подключения: «В этом случае эквивалентными рёбрами, через которые будет течь одинаковый ток, являются рёбра AC и AB» может вместо АВ правильно будет АD? Или нет?
Да, спасибо за ваше замечание. Исправил.
В жизни не оставлял комментариев, но здесь случай исключительный, спасибо!
Спасибо за подробное объяснение!
Премного благодарен вам. Спасибо
Рад, что материал оказался для вас полезным.
Отлично, коротко и ясно
Спасибо огромное
Спасибо за понятное объяснение
Долго пытался решить подобную задачу. Но не смог.
(1 вариант). Вы все понятно объяснили. Теперь смогу решать подобные задачи.
Спасибо за объяснение!
Спасибо огромное!