В данной статье речь пойдёт о том, как выразить площадь многоугольника, в который можно вписать окружность, через радиус этой окружности. Сразу стоит отметить, что не во всякий многоугольник можно вписать окружность. Однако, если это возможно, то формула, по которой вычисляется площадь такого многоугольника, становится очень простой. Дочитайте эту статью до конца или посмотрите прилагающийся видеоурок, и вы узнаете, как же выразить площадь многоугольника через радиус вписанной в него окружности.
Формула площади многоугольника через радиус вписанной окружности
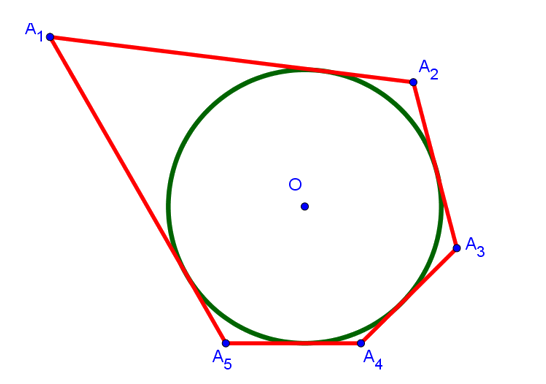
Нарисуем многоугольник A1A2A3A4A5, не обязательно правильный, но такой, в который можно вписать окружность. Напомню, что вписанной называется окружность, которая касается всех сторон многоугольника. На рисунке это зелёная окружность с центром в точке O:
Мы взяли здесь для примера 5-угольник. Но на самом деле это не имеет существенного значения, поскольку дальнейшее доказательство справедливо и для 6-угольника и для 8-угольника и вообще для любого сколь угодно «угольника».
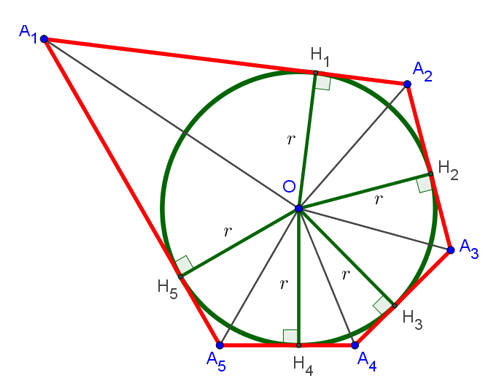
Если соединить центр вписанной окружности со всеми вершинами многоугольника, то он разобьётся на столько треугольников, сколько вершин в данном многоугольнике. В нашем случае: на 5 треугольников. Если же соединить точку O со всеми точками касания вписанной окружности со сторонами многоугольника, то получится 5 отрезков (на рисунке снизу это отрезки OH1, OH2, OH3, OH4 и OH5), которые равны радиусу окружности и перпендикулярны сторонам многоугольника, к которым они проведены. Последнее справедливо, поскольку радиус, проведенный в точку касания, перпендикулярен касательной:
Как же найти площадь нашего описанного многоугольника? Ответ прост. Нужно сложить площади всех полученных в результате разбиения треугольников:
![]()
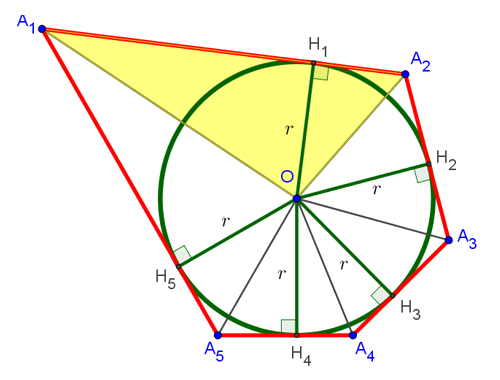
Рассмотрим, чему равна площадь треугольника ![]() . На рисунке снизу он выделен жёлтым цветом:
. На рисунке снизу он выделен жёлтым цветом:
Она равна половине произведения основания A1A2 на высоту OH1, проведённую к этому основанию. Но, как мы уже выяснили, эта высота равна радиусу вписанной окружности. То есть формула площади треугольника принимает вид: ![]() , где r — радиус вписанной окружности. Аналогично находятся площади всех оставшихся треугольников. В результате искомая площадь многоугольника оказывается равна:
, где r — радиус вписанной окружности. Аналогично находятся площади всех оставшихся треугольников. В результате искомая площадь многоугольника оказывается равна:
![]()
![]()
Видно, что во всех слагаемых этой суммы ест общий множитель ![]() , который можно вынести за скобки. В результате получится вот такое выражение:
, который можно вынести за скобки. В результате получится вот такое выражение:
![]()
То есть в скобках осталась просто сумма всех сторон многоугольника, то есть его периметр P. Чаще всего в этой формуле выражение ![]() заменяют просто на p и называют эту букву «полупериметром». В результате, окончательная формула принимает вид:
заменяют просто на p и называют эту букву «полупериметром». В результате, окончательная формула принимает вид:
![]()
То есть площадь многоугольника, в который вписана окружность известного радиуса, равна произведению этого радиуса на полупериметр многоугольника. Это и есть тот результат, в которому мы стремились.
Отметит напоследок, что в треугольник, который является частным случаем многоугольника, всегда можно вписать окружность. Поэтому для треугольника эту формулу можно применять всегда. Для остальных многоугольников, с количеством сторон большим 3, сперва нужно убедиться, что в них можно вписать окружность. Если это так, можно смело использовать эту простую формулу и находить по ней площадь этого многоугольника.
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич

Какого учёного носит имя эта теорема?
Как называется эта теорема?
Спасибо, помогли! готовлюсь к егэ, нигде не мог найти эту формулу